参考QT官方文档

前言:使用qt6.2.4 qml的CMake工程时遇到qrc中的qml文件和图片无法使用的情况,查了好久终于找到解决办法,在此记录一下

1. 新建qml.qrc资源文件

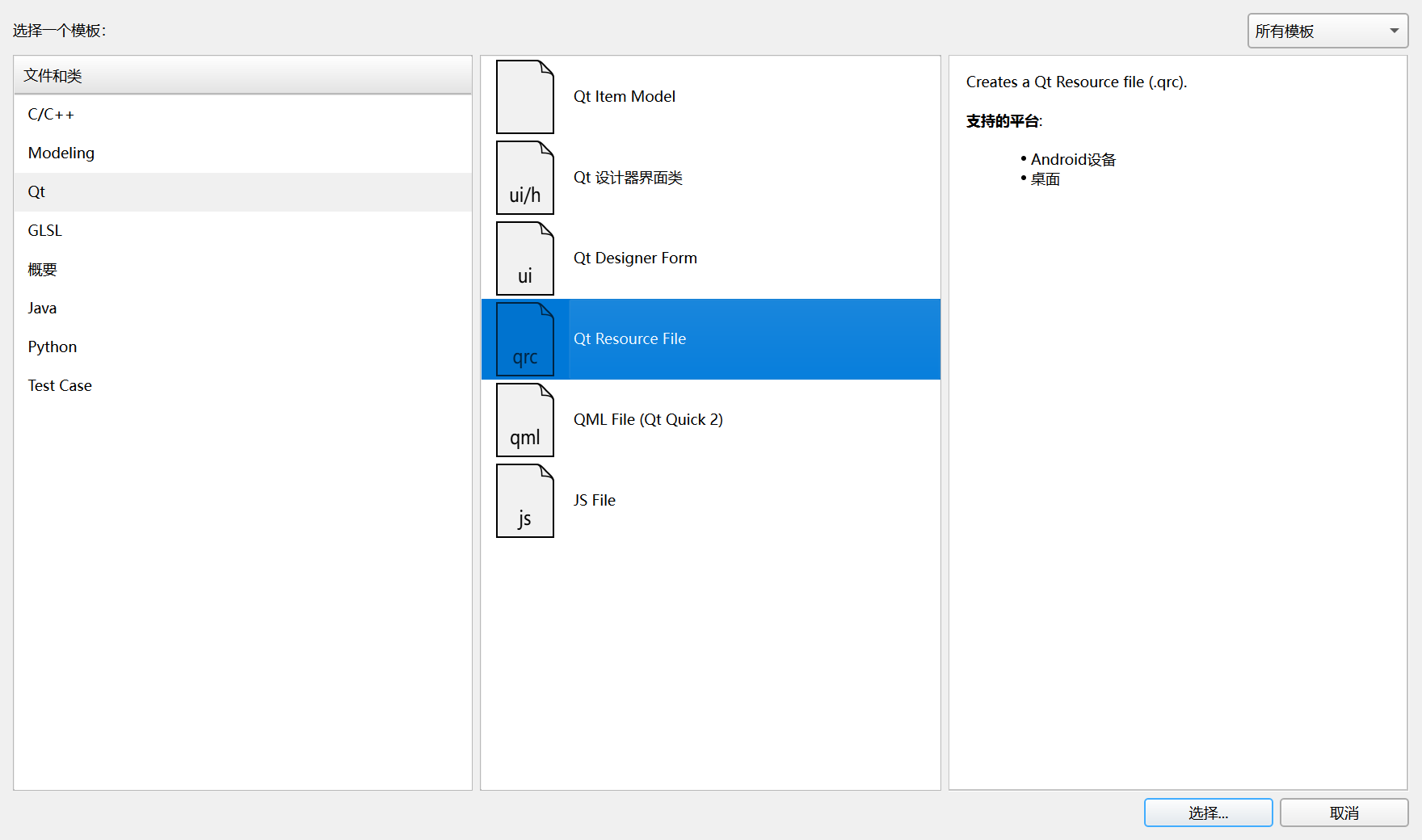
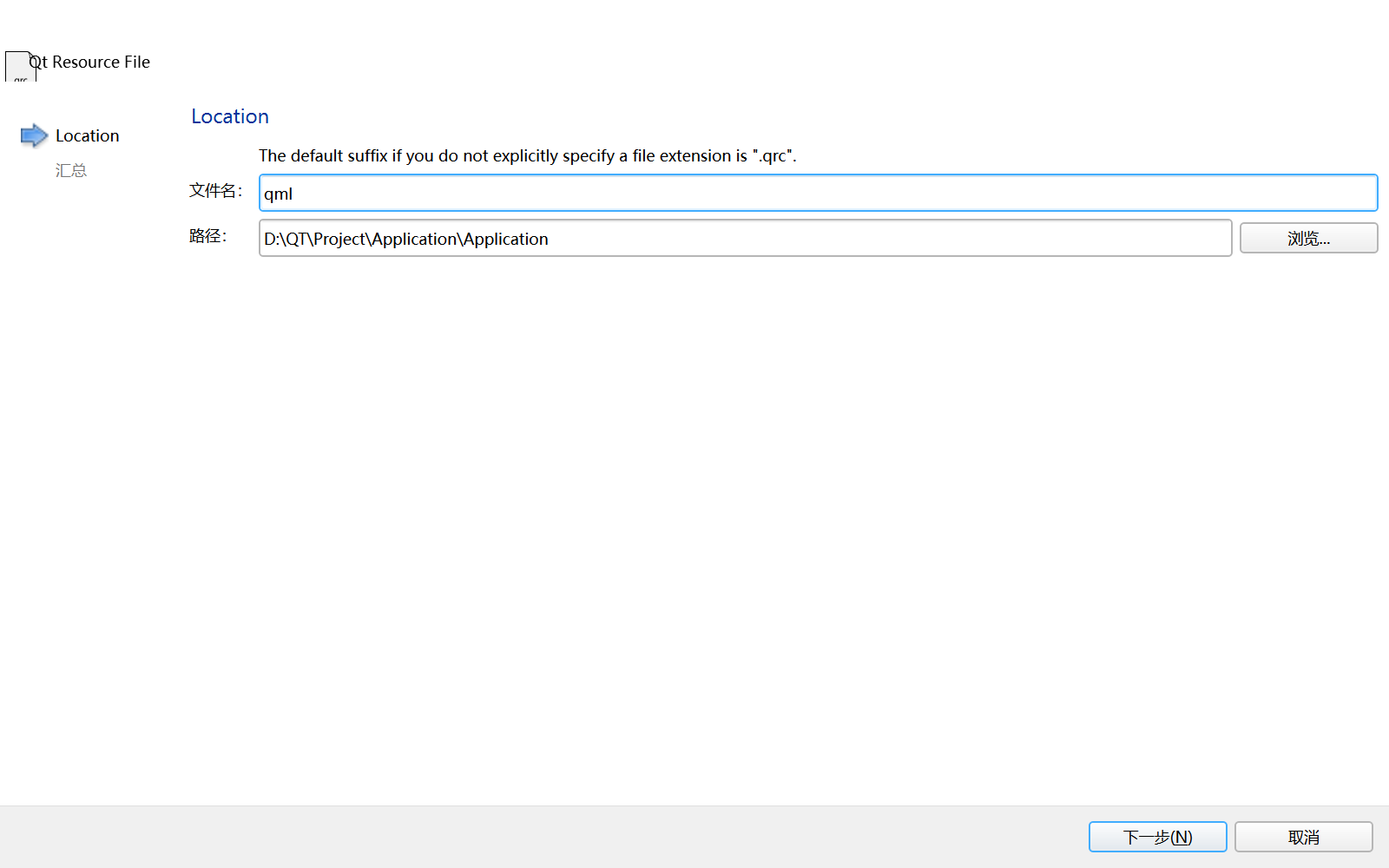
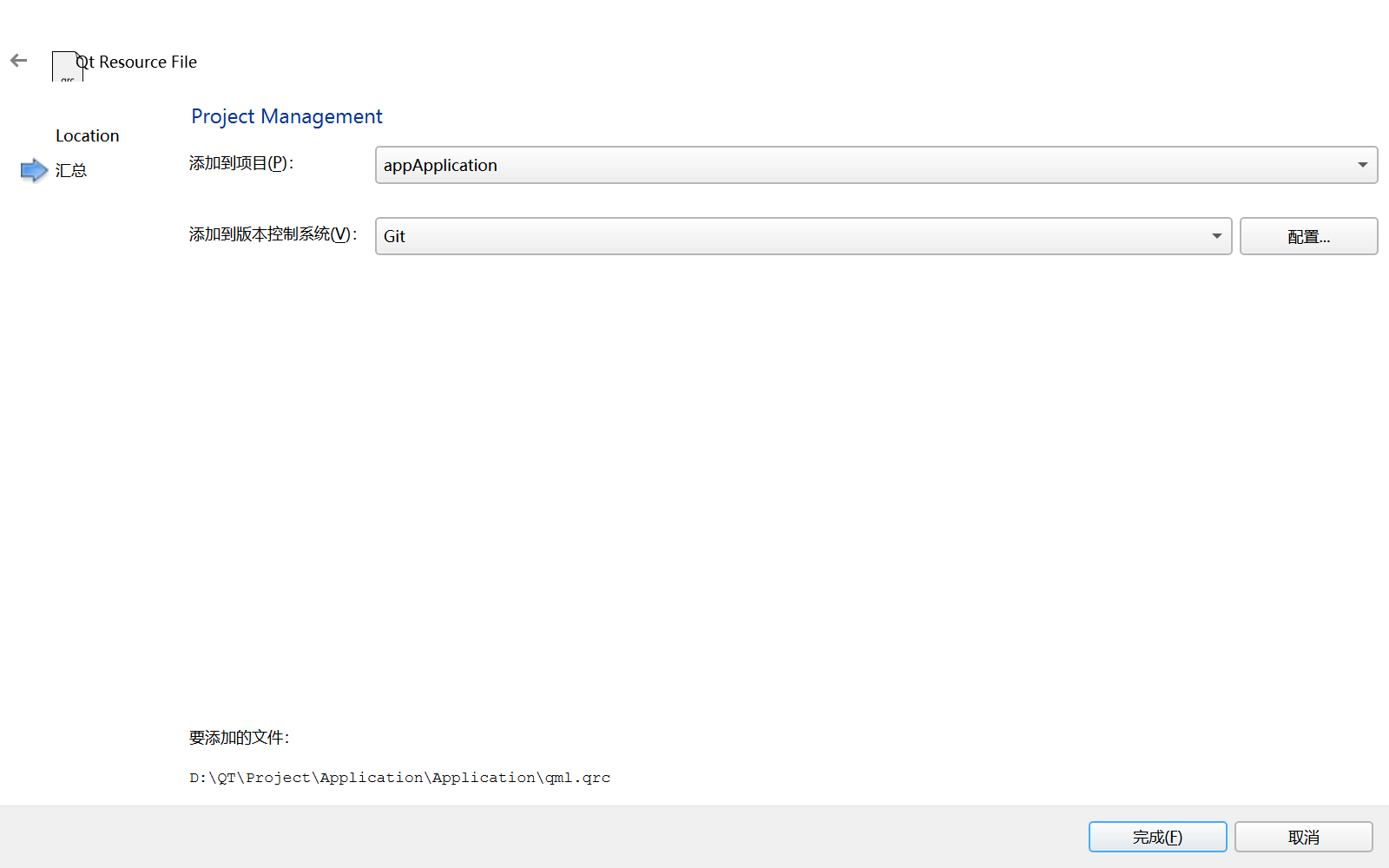
可以在目录下看到qrc文件表示新建成功

2.给qrc文件添加前缀

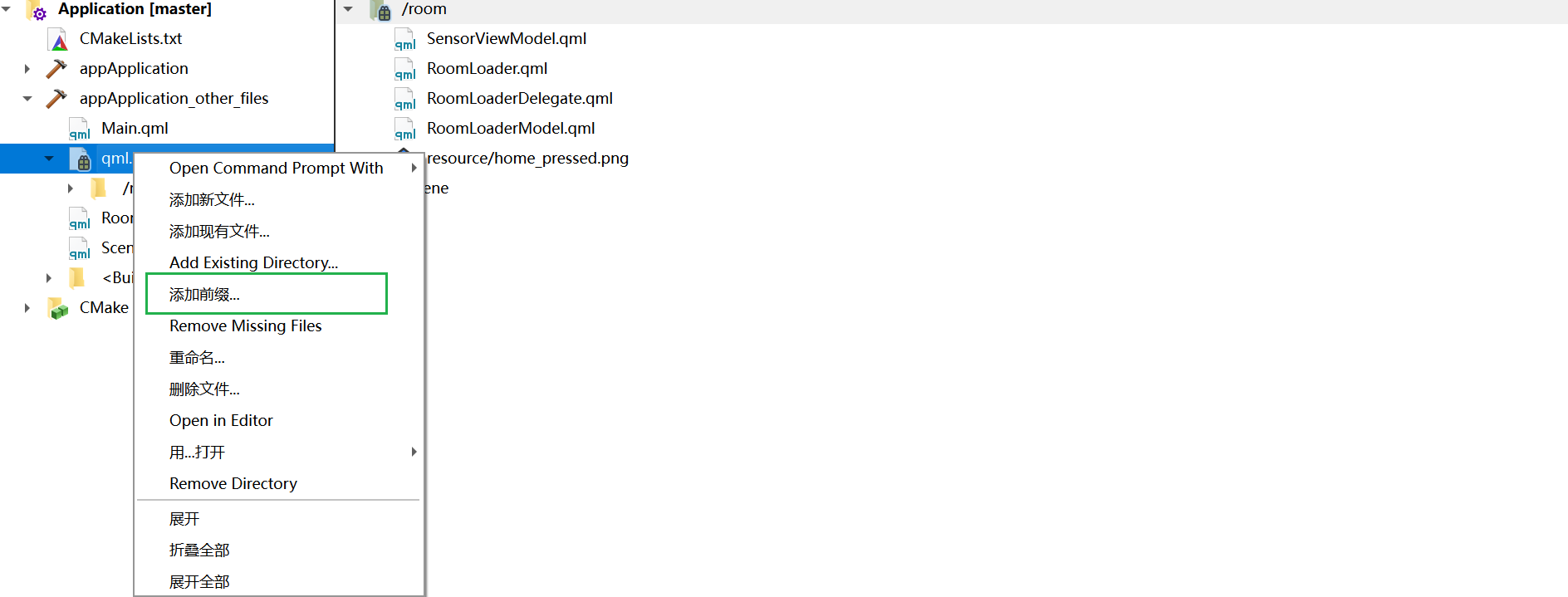
添加完成后如下:

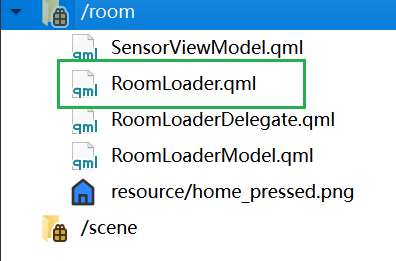
3. 修改CMakeLists.txt

我需要在一个qml文件中使用Loader组件加载另一个qml组件代码如下:

CMakeList中没加代码之前会出现找不到qml文件的报错

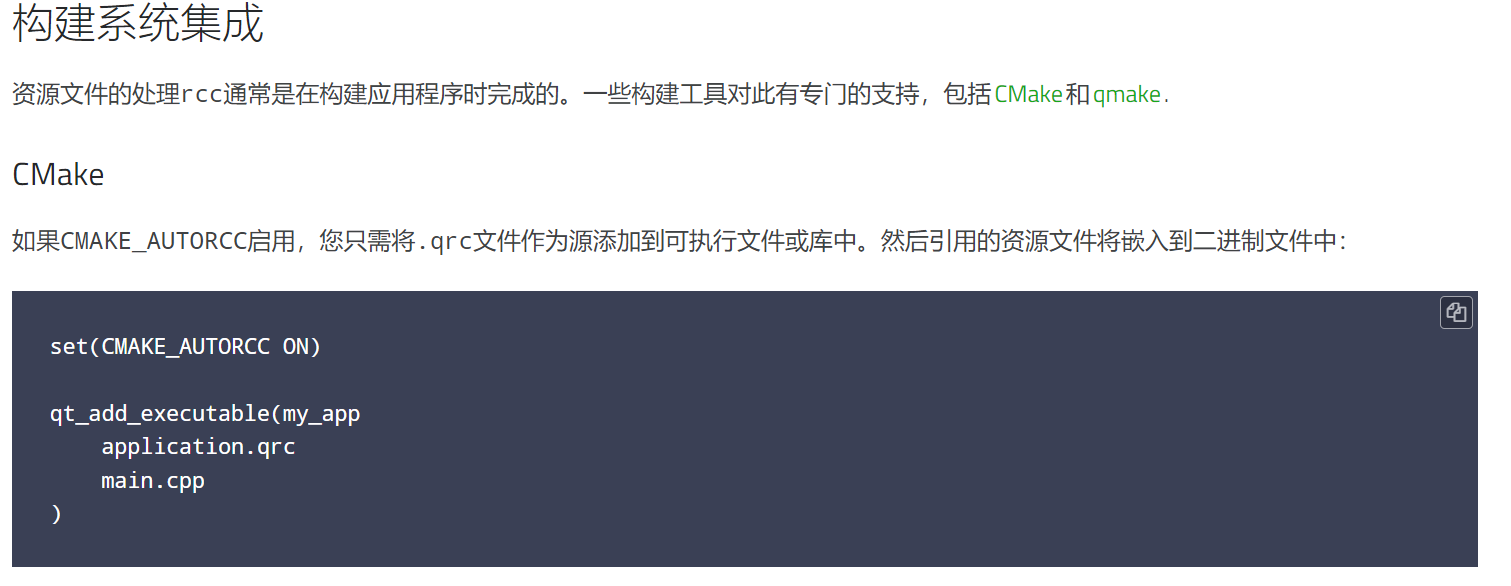
在CMakeLists.txt中添加如下代码后qml文件成功加载

set(CMAKE_AUTORCC ON)
qt_add_executable(appApplication //工程名称
    main.cpp
    qml.qrc //新建的qrc资源文件
)

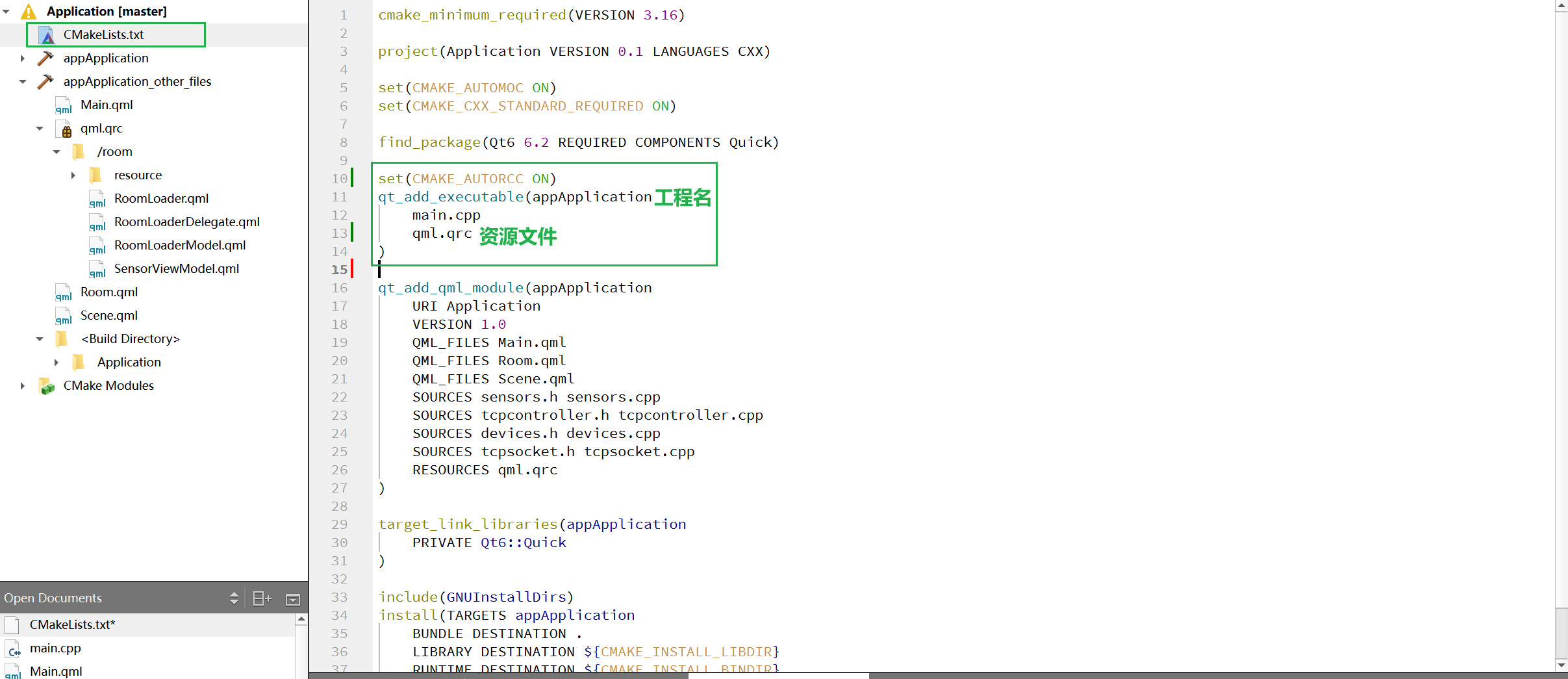
参考如下: