GSS3 - Can you answer these queries III

题面翻译

$n$ 个数， $q$ 次操作

操作0 x y把 $A_x$ 修改为 $y$

操作1 l r询问区间 $[l, r]$ 的最大子段和

感谢 @Edgration 提供的翻译

题目描述

You are given a sequence A of N (N <= 50000) integers between -10000 and 10000. On this sequence you have to apply M (M <= 50000) operations:
modify the i-th element in the sequence or for given x y print max{Ai + Ai+1 + … + Aj | x<=i<=j<=y }.

输入格式

The first line of input contains an integer N. The following line contains N integers, representing the sequence A1…AN.
The third line contains an integer M. The next M lines contain the operations in following form:
0 x y: modify Ax into y (|y|<=10000).
1 x y: print max{Ai + Ai+1 + … + Aj | x<=i<=j<=y }.

输出格式

For each query, print an integer as the problem required.

样例 #1

样例输入 #1

样例输出 #1

6
4
-3

分析

线段树，但维护什么呢？可以维护一个最大子段和，那么见下图：

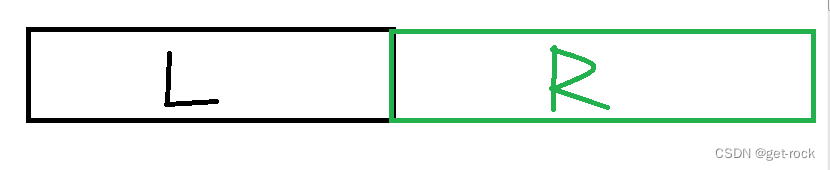
线段树把区间分成两段，这里叫L，R吧，可以得出最大子段和： $maxn=\max{L_{maxn}},{R_{maxn}}$
但这两种情况仍不足，可能最大子段和来自L和R，如图
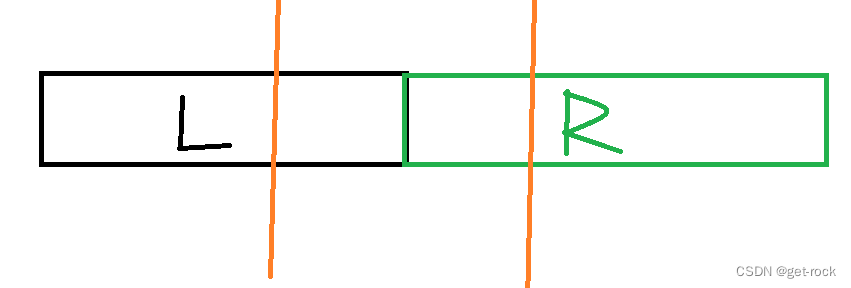
在这里插入图片描述

故应维护最大前缀和pre,与最大后缀和suf，得出公式 $maxn=\max\{{L_{maxn}},{R_{maxn}},L_{suf}+R_{pre}\}$
那么怎么维护pre与suf呢，不难想到：
$pre=\max L_{pre},L_{sum}+R_{pre}$
$suf=\max R_{suf},L_{suf}+R_{sum}$
需要维护区间和sum

代码

#include <bits/stdc++.h>
using namespace std;
const int M = 1e5+10;
int a[M],n,m;
void read(){
	cin>>n;
	for (int i=1;i<=n;i++) cin>>a[i];	
	cin>>m;
}
struct node{
	int maxn,pre,suf,sum;
};
struct segment{
	#define rc(x) ((x<<1)|1)
	#define lc(x) (x<<1)
	node seg[M<<2];
	void push_up(int x){
		int l=lc(x),r=rc(x);
		seg[x].sum=seg[l].sum+seg[r].sum;
		seg[x].pre=max(seg[l].pre,seg[l].sum+seg[r].pre);
		seg[x].suf=max(seg[r].suf,seg[r].sum+seg[l].suf);
		seg[x].maxn=max(max(seg[l].maxn,seg[r].maxn),seg[l].suf+seg[r].pre);
	}
	void build(int o,int l,int r){
		if (l==r) {
			seg[o].maxn=seg[o].pre=seg[o].suf=seg[o].sum=a[l];
			return;
		}
		int mid=l+r>>1;
		build(lc(o),l,mid);
		build(rc(o),mid+1,r);
		push_up(o);
	}
	void update(int x,int y,int o=1,int l=1,int r=n){
		if (l==r and l==x) {
			seg[o].maxn=seg[o].pre=seg[o].suf=seg[o].sum=y;
			return;
		}
		if (x<l or r<x) return;
		int mid=l+r>>1;
		update(x,y,lc(o),l,mid);
		update(x,y,rc(o),mid+1,r);
		push_up(o);
	}
	node query(int ql,int qr,int o=1,int l=1,int r=n){
		if (ql<=l and r<=qr) return seg[o];
		int mid=l+r>>1;bool f1=0,f2=0;
		node left,right;
		if (ql<=mid) left=query(ql,qr,lc(o),l,mid),f1=1;
		if (mid+1<=qr) right=query(ql,qr,rc(o),mid+1,r),f2=1;
		node ans;
		if (f1 and f2){
			ans.sum=left.sum+right.sum;
			ans.pre=max(left.pre,left.sum+right.pre);
			ans.suf=max(right.suf,right.sum+left.suf);
			ans.maxn=max(max(left.maxn,right.maxn),left.suf+right.pre);
		}
		else if(f1) ans=left;
		else ans=right;
		return ans;
	}
}T1;
void solve(){
	int x,y,z;
	cin>>z>>x>>y;
	if(z) cout<<T1.query(x,y).maxn<<endl;
	else T1.update(x,y);
}
int main(){
	read();
	T1.build(1,1,n);
	while(m--) solve();
	return 0;
}

分析

	node query(int ql,int qr,int o=1,int l=1,int r=n){
		if (ql<=l and r<=qr) return seg[o];
		int mid=l+r>>1;bool f1=0,f2=0;
		node left,right;
		if (ql<=mid) left=query(ql,qr,lc(o),l,mid),f1=1;
		if (mid+1<=qr) right=query(ql,qr,rc(o),mid+1,r),f2=1;
		node ans;
		if (f1 and f2){
			ans.sum=left.sum+right.sum;
			ans.pre=max(left.pre,left.sum+right.pre);
			ans.suf=max(right.suf,right.sum+left.suf);
			ans.maxn=max(max(left.maxn,right.maxn),left.suf+right.pre);
		}
		else if(f1) ans=left;
		else ans=right;
		return ans;
	}