今日份题目：

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例1

输入：numbers = [3,4,5,1,2]
输出：1

示例2

输入：numbers = [2,2,2,0,1]
输出：0

提示

n == numbers.length
1 <= n <= 5000
-5000 <= numbers[i] <= 5000
numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

题目思路

方法一：暴力搜索

从头到尾遍历数组，如果没有旋转的话应该从头到尾是递增数列，所以如果遇到某个数比前一个数小，那么这个数就是要找的最小的那个旋转的数，如果全程找不到那最小的那个旋转数就是第一个数。

代码

class Solution 
{
public:
    int minArray(vector<int>& numbers) 
    {
        int pre,cur;
        int n=numbers.size();
        if(n==1) return numbers[0];//注意先判断长度，如果只有一个元素，那么运行cur=numbers[1]会出错
        pre=numbers[0];
        cur=numbers[1];
        if(cur<pre) return cur;
        for(int i=2;i<n;i++)
        {
            pre=cur;
            cur=numbers[i];
            if(cur<pre) return cur;
        }
        return numbers[0];
    }
};

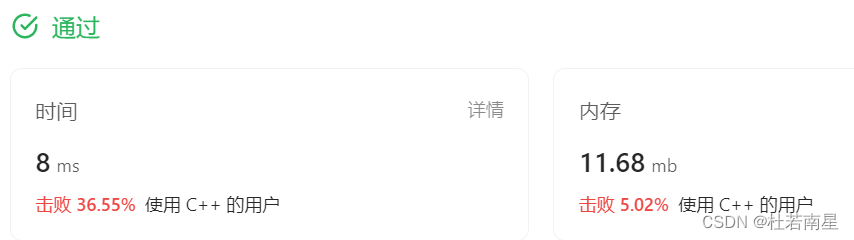
提交结果

方法二：二分查找（官方给出）

numbers[mid]和numbers[r]之间会出现三种情况

第一种情况是 numbers[mid]<numbers[r]。如下图所示，这说明 numbers[mid]是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

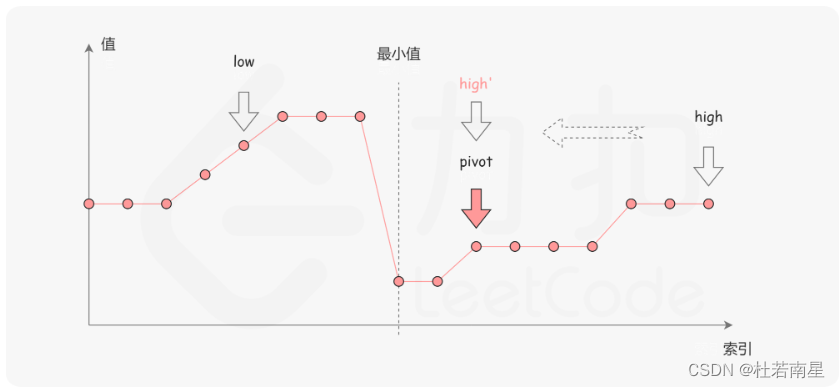
第二种情况是 numbers[mid]>numbers[r]。如下图所示，这说明 numbers[mid]是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

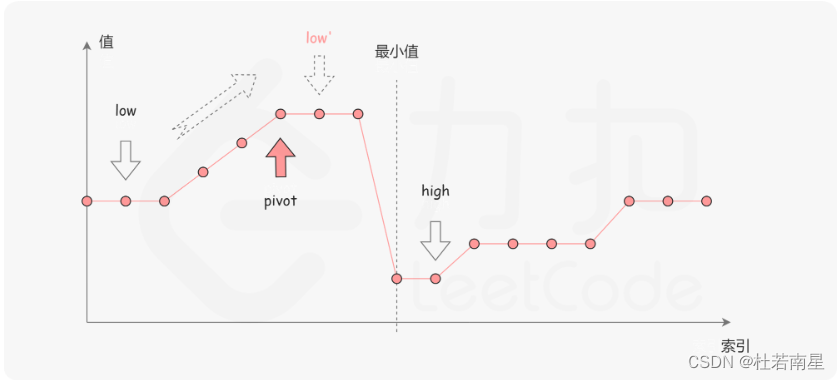
第三种情况是 numbers[mid]==numbers[r]。如下图所示，由于重复元素的存在，我们并不能确定 numbers[mid]究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论 numbers[r]是不是最小值，都有一个它的「替代品」numbers[mid]，因此我们可以忽略二分查找区间的右端点。

（思路来源：作者：力扣官方题解链接：力扣来源：力扣（LeetCode））

代码

class Solution 
{
public:
    int minArray(vector<int>& numbers) 
    {
        int n=numbers.size()
        int l=0,r=n-1;
        while(l<=r) 
        {
            int mid=(l+r)/2;
            if(numbers[mid]<numbers[r]) r=mid;
            else if(numbers[mid]>numbers[r]) l=mid+1;
            else r--; 
        }
        return numbers[l];
    }
};