EMD概述
其实一种信号分解方法,是一种自适应的数据处理方法,适合非线性和非平稳时间序列的分析和研究,其本质是对数据序列或信号的平稳化处理。

将上面6个信号叠加如下:

就是6个简单信号叠加,形成一个复杂信号。
核心思想
经验模态分解就是把观察到的时间序列分解为有限个序列,每个序列具有某种特征,就是上面过程的逆过程,将复杂图片分解为简单图片。

第一个信号加第二个信号就合成了第三个杂乱无章的信号。
基本步骤
1.找到信号的局部最大值和局部最小值,局部最大值为红点,局部最小值为绿点:

2.用二次样条函数或者直接用直线拟合起来:

3.求得平均线(黑线):(红线+绿线)/2

4.用原始信号减去黑线,如下:

5.重复1~3步:

6.然后在用第4步的线减去第五步的黑线:

7.继续重复以上步骤
8.中止条件:
 知道零点以下没有两个连续的极大值和极小值,此时的曲线叫做残差项。
知道零点以下没有两个连续的极大值和极小值,此时的曲线叫做残差项。
原始线减去黑线这类线叫做IMF,最上面的曲线可以分解为IMF1+IMF2+....+IMFN+残差项。
和其他方法的对比
无论是傅里叶变换还是小波分解,他们分解的信号都是从-inf~inf,这一点在实际中无法实现。
经验模态分解没有基函数,小波和傅里叶分解都有基函数,从这个角度来讲,经验模态分解是一种自适应分解方法。导致数据分解分解出来的若干个信号非常有限。
正常情况下,一般分解最多可以到15个IMF,正常情况下是分解到6个IMF。
经验模态分解没有严格的数学理论作为基础支撑。
应用案例:带合成的经验模态分解方法与新的原油价格形成机制理论
原油价格由什么决定: (是由什么决定的,供求关系对原油关系的占比多大)
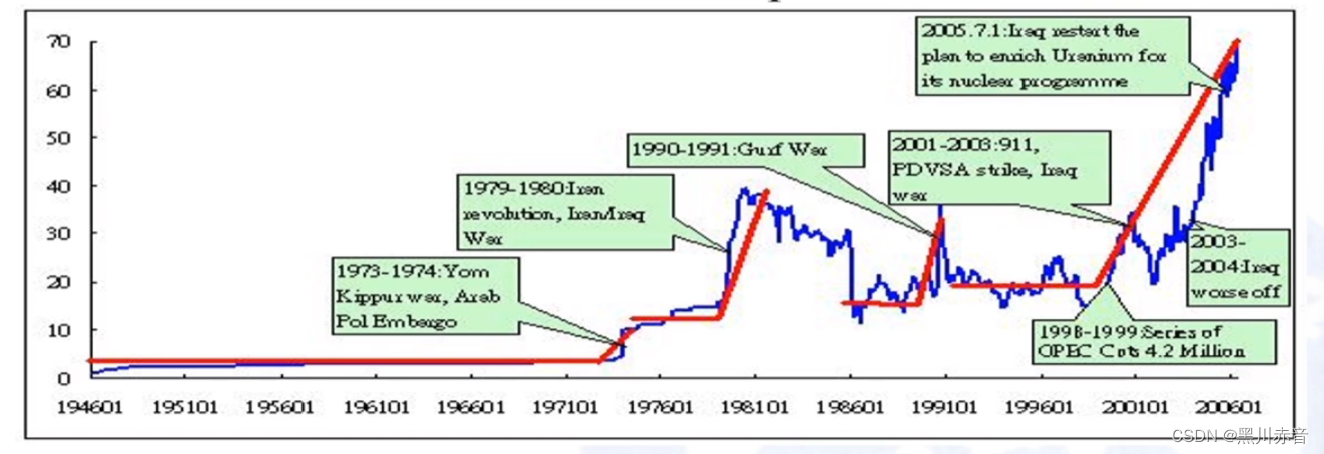
1973年之前的价格都是平的,后面产生烈波动时都发生了战争,下面把该图片压扁即为:

然后进行经验模态分解:
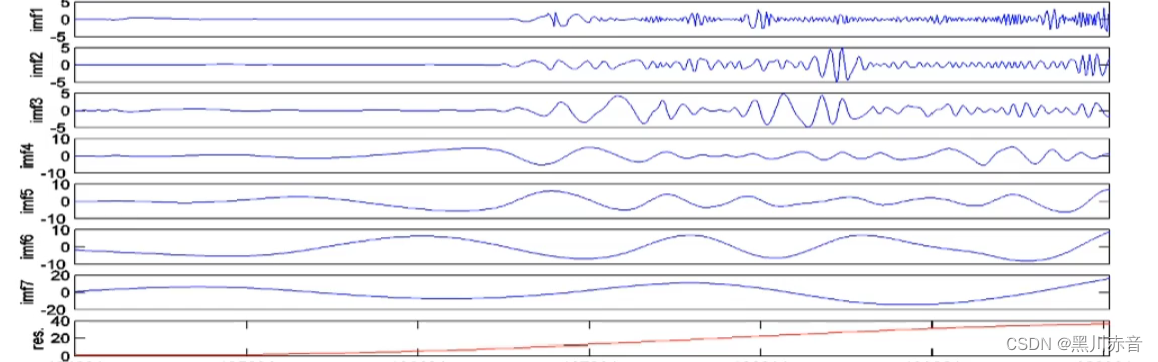
然后就看到残差曲线(红线),假定红线是供求关系对原油价格的影响(因为原油的需求是越来越多了)。
IMF1~IMF7是一个高频到低频的过度,
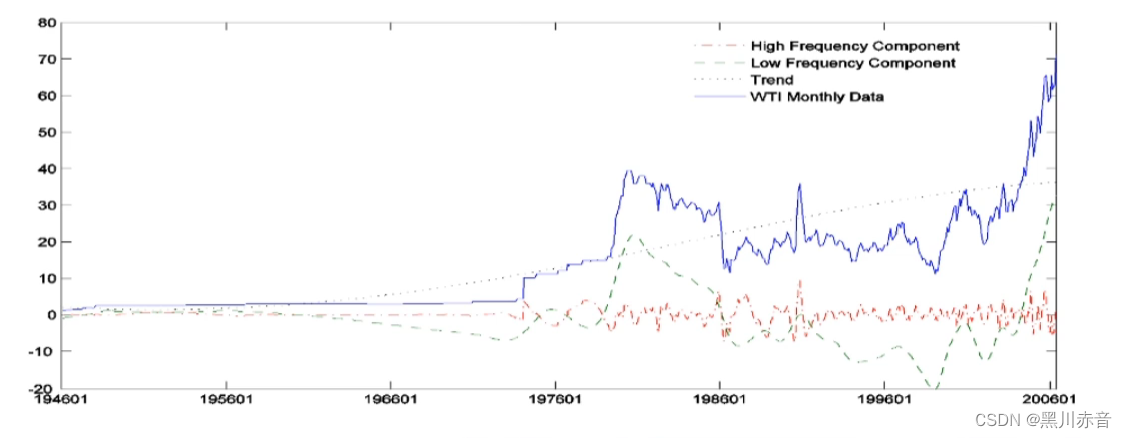
然后绿线是低频合成的曲线,红线是高频合成的曲线,蓝线是原始曲线。绿线上的拐点和重大的曲线上发生重大事件的节点对应起来了。
因此,原油价格的波动有3个原因:1.供求关系 2.对短期造成影响的事件(红线,基金炒作,货币政策调整等事件) 3.对长期造成影响的事件。
结论是得到了原油价格的定价理论。
EEMD概述
EMD会产生模态混叠现象,即一个IMF的信号频带会很宽,涵盖了低频和高频信号,实际中,我们希望某一个IMF信号的频带尽可能集中。
EEMD(ensemble empirical mode decomposition)由于白噪声的尺度特征在整个时频域上均匀分布,进行EMD分解时,各种尺度特征中都会含有白噪声的成份。如果给信号添加白噪声后进行分解,那么信号含有的某种尺度特征,会被分解到与白噪声相对应的尺度特征上去。虽然噪声的不确定性,使得其在单次分解时,可能影响到信号的分解结果,但根据白噪声的统计特性,如果添加不同的白噪声,对大量分解结果求均值,各尺度特征中的噪声成份会相互抵消,最后只剩下待分解信号。
EEMD的实施步骤如下:

具体优势:
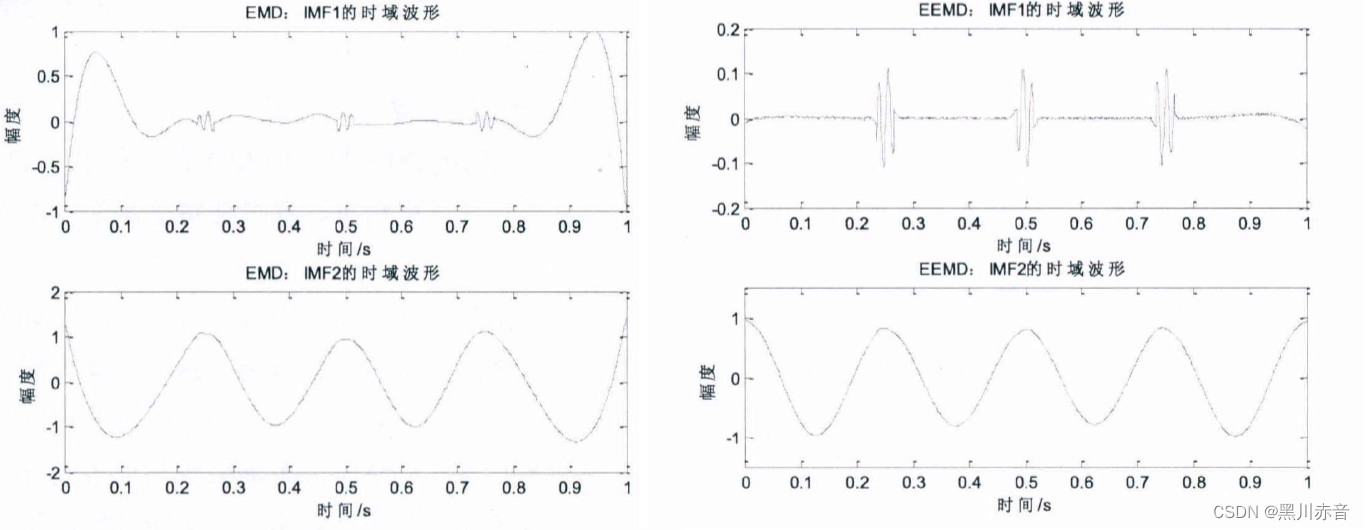
可以看到,EEMD频带更加集中。
CCEMD概述
CCEMD(complementary ensemble empirical mode decomposition),添加的高斯白噪声都是互补的,即满足:,一对一对的对噪声进行添加。
CEEMDAN概述

小结论:CEEMDAN和EEMD比CEEMD,EMD效果要好,CEEMDAN的运算速度比EEMD更快。
代码实现(pip install EMD-signal):
EMD实现:
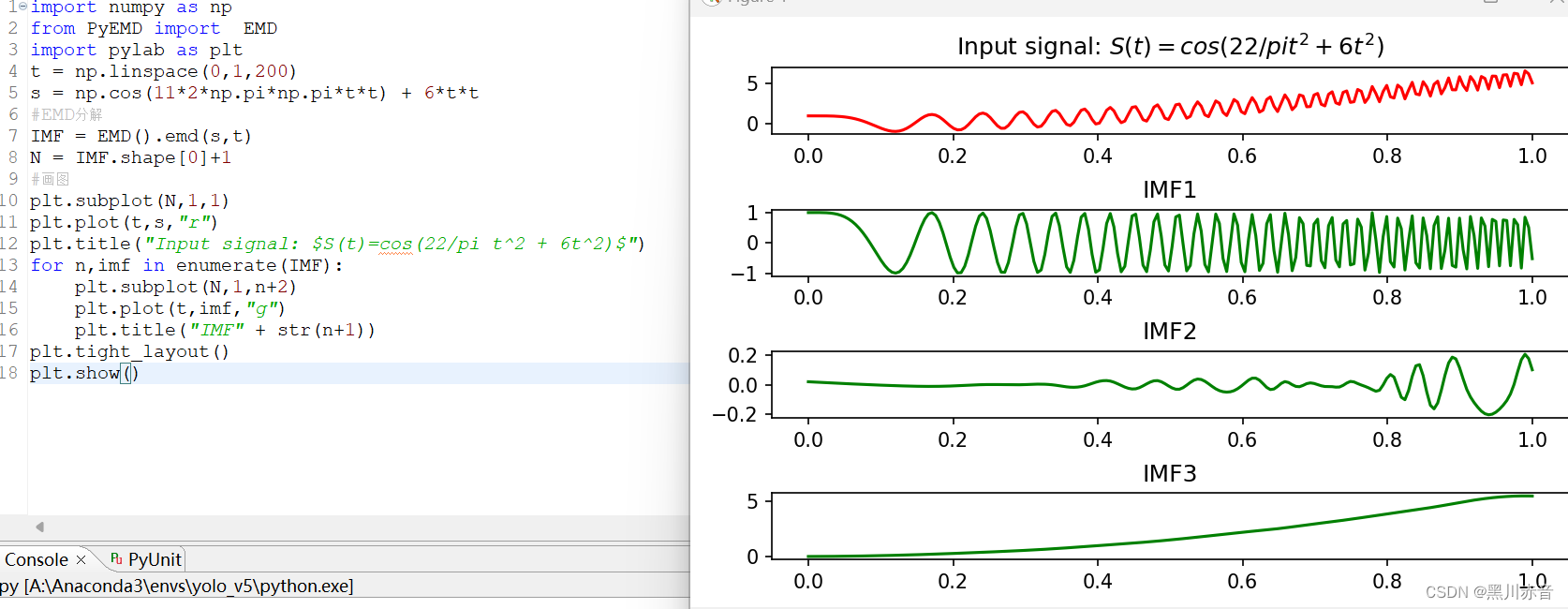
import numpy as np
from PyEMD import EMD
import pylab as plt
t = np.linspace(0,1,200)
s = np.cos(11*2*np.pi*np.pi*t*t) + 6*t*t
#EMD分解
IMF = EMD().emd(s,t)
N = IMF.shape[0]+1
#画图
plt.subplot(N,1,1)
plt.plot(t,s,"r")
plt.title("Input signal: $S(t)=cos(22/pi t^2 + 6t^2)$")
for n,imf in enumerate(IMF):
plt.subplot(N,1,n+2)
plt.plot(t,imf,"g")
plt.title("IMF" + str(n+1))
plt.tight_layout()
plt.show()EEMD实现:
import numpy as np
from PyEMD import EEMD
import pylab as plt
t = np.linspace(0,1,200)
s = np.cos(11*2*np.pi*np.pi*t*t) + 6*t*t
#EEMD分解
eemd = EEMD()
emd = eemd.EMD
emd.extrema_detection = "parabol"
IMF = eemd.eemd(s,t)
N = IMF.shape[0]+1
#画图
plt.subplot(N,1,1)
plt.plot(t,s,"r")
plt.title("Input signal: $S(t)=cos(22/pi t^2 + 6t^2)$")
for n,imf in enumerate(IMF):
plt.subplot(N,1,n+2)
plt.plot(t,imf,"g")
plt.title("IMF" + str(n+1))
plt.tight_layout()
plt.show()