文章链接：https://arxiv.org/abs/2101.02824

参考博客：https://arxiv.org/abs/2101.02824

1. 方法原理

1.1 先前方法总结

1. 监督学习的方法：noisy-clean训练方法数据集构建存在问题、泛化性不好，真实场景基本用不了。
2. Noise2Noise系列：每个场景需要配对的噪声数据。应用上会有局限性，比如室内静态场景。
3. 现有的自监督学习方法：
   • 从单张图片上挖掘信息：DIP系列，Self2Self，Noisy-as-Clean
   • Noise2Noise系列：N2N，Noise2Void，Noise2Self，问题在于网络训练困难、会损失有用信息、依赖于噪声模型
   • 噪声建模方法：Probabilistic Noise2Void，Laine19,Dilated Blind-Spot预测噪声分布，在实际中很难应用

1.2 Noise2Noise回顾

Noise2Noise不需要噪声图片，基于多张独立的噪声图像就去噪, 具体内容可以参考:Noise2Noise 笔记

• Noise2Noise的局限在于：需要采集同一个场景下多个图像，着对于动态场景（户外或者自拍）是非常困难的。

• Neighbor2Nieghbor的动机就是解决上述问题，有两个假设/想法：

  1. Noise2Noise是对同一场景进行多次采样训练 --> 对相似的场景进行多个采样然后进行训练 --> 降低数据采集的难度
  2. 是否能够只使用一张含噪声图像就训练网络

1.3 从Noise2Noise到Neighbor2Neighbor

Noise2Noise的最大似然估计
$$\underset{\theta }{\mathrm{argmin}}{E}_{x,y,z}||f_{\theta }(y)-z||$$

由于Noise2Noise要求一个场景(x)至少两个独立含噪的图片($y，z$)，这在真实场景中很难满足，所以需要考虑扩展理论：

• 同一场景两个独立含噪图像 --> 相似场景两张独立含噪声图像
• 每个场景多张含噪图像–> 每个场景单张含噪图像

相似场景配对噪声图片进行去噪

将 Noise2Noise的概念拓展一下：假设有一张干净图片$x$, 一张含噪图像是$y$，另一张含噪图像z上还有一些别的偏差
$$ϵ:=E_{z|x}(z)-E_{y|x}(y)\ne 0$$

第一个定理：用 y和z表示x上的两个噪声数据，并且考虑$ϵ\ne 0$： $E_{y|x}(y)=x$ 和 $E_{z|x}(z)=x+ϵ$, 其中z的方差为 ${\sigma }_z^2$。那么有:
$$E_{x,y}||f_{\theta }(y)-x|{|}_2^2=E_{x,y,z}||f_{\theta }(y)-z|{|}_2^2-{\sigma }_z^2+2ϵE_{x,y}(f_{\theta }(y)-x)$$

• 当噪声图片之间的偏差 $ϵ\ne 0$的时候（也就是$E_{x,y}（f_{\theta }(y)-x）\ne 0$）,优化Noise2Noise网络的 $E_{x,y,z}||f_{\theta }(y)-z|{|}_2^2$不会得到和监督学习 $E_{x,y}(f_{\theta }(y)-x)$ 相同的结果。
• 但是当$ϵ\to 0$时，$2ϵE_{x,y}(f_{\theta }(y)-x)\to 0$, 也就是说Noise2Noise网络训练的结果和监督学习训练的结果是近似的。（这里需要注意一个点，${\sigma }_z$是一个常数，优化过程不影响）

上面其实是Noise2Noise工作的原理,但是需要一对噪声数据
  对于单张含噪图像而言，构造两张"相似但不相同"的图像的一种可行方法是采样。在原图的相邻但不相同的位置采样出来的子图很显然满足了相互之间的差异很小，但是其对应的干净图像并不相同的条件($ϵ\to 0$)。给定含噪图像y，我们从中采样两次得到噪声对（$g_1(y),g_2(y)$），用Noise2Noise的方式训练有：
$$\underset{\theta }{\mathrm{argmin}}{E}_{x,y}||f_{\theta }(g_1(y))-g_2(y)|{|}^2$$

这种方法称为 Pseudo Noise2Noise ,但是由于 $g_1(y),g_2(y)$ 采样的位置不同，其偏差不等于0:
$$ϵ=E_{y|x}(g_2(y))-E_{y|x}(g_1(y))\ne 0$$

直接用Noise2Noise的方法训练得到的结果不是理想结果，且容易导致过度平滑。因此Neighbor2Neighbor考虑在其上加正则项进行约束。假设一个理想的降噪网络 $f_{\theta }^{\ast }$，其具有理想降噪能力
$$f_{\theta }^{\ast }(y)=x$$

$$f_{\theta }^{\ast }(g_l(y))=g_l(x)$$

这个理想的降噪网络满足：

E y ∣ x { f θ ∗ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ∗ ( y ) ) − g 2 ( f θ ∗ ( y ) ) ) } = g 1 ( x ) − E y ∣ x { g 2 ( y ) } − ( g 1 ( x ) − g 2 ( x ) ) = g 2 ( x ) − E y ∣ x { g x ( y ) } = 0 \begin{aligned} &E_{y|x} \{ f_{\theta}^* (g_1(y)) - g_2(y) - (g_1(f_{\theta}^*(y)) -g_2(f_{\theta}^*(y))) \}\\ &= g_1(x) - E_{y|x}\{ g_2(y)\} - (g_1(x) - g_2(x)) \\ &= g_2(x) - E_{y|x}\{ g_x(y)\} \\ &= 0 \end{aligned} ​Ey∣x​{fθ∗​(g1​(y))−g2​(y)−(g1​(fθ∗​(y))−g2​(fθ∗​(y)))}=g1​(x)−Ey∣x​{g2​(y)}−(g1​(x)−g2​(x))=g2​(x)−Ey∣x​{gx​(y)}=0​

因此考虑在 Pseudo Noise2Noise网络中添加一个约束
$$\underset{\theta }{\mathrm{argmin}}{E}_{y|x}||f_{\theta }(g_1(y))-g_2(y)|{|}_2^2$$

s . t .      E y ∣ x { f θ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ( y ) ) − g 2 ( f θ ( y ) ) ) } = 0 s.t. \;\; E_{y|x} \{ f_{\theta} (g_1(y)) - g_2(y) - (g_1(f_{\theta}(y)) -g_2(f_{\theta}(y))) \} = 0 s.t.Ey∣x​{fθ​(g1​(y))−g2​(y)−(g1​(fθ​(y))−g2​(fθ​(y)))}=0

最后将带约束的优化转换为带正则的优化问题：
$$\underset{\theta }{\mathrm{argmin}}{E}_{y|x}||f_{\theta }(g_1(y))-g_2(y)|{|}_2^2+\gamma E_{y|x}||f_{\theta }(g_1(y))-g_2(y)-(g_1(f_{\theta }(y))-g_2(f_{\theta }(y)))|{|}_2^2$$

1.4 框架结构

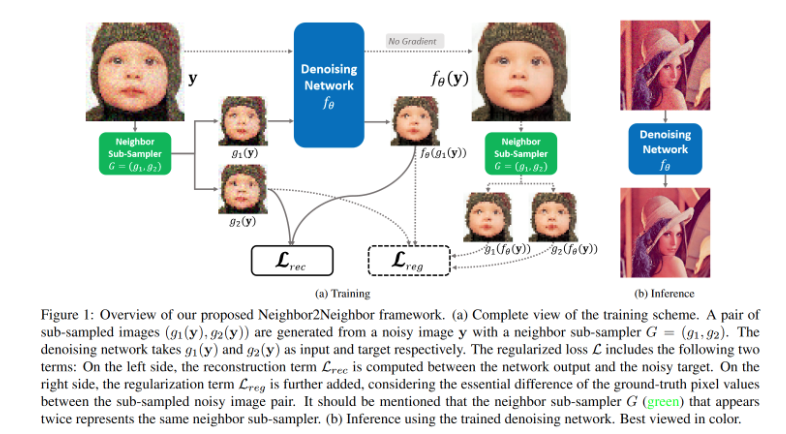
具体而言：

1. 从单张含噪图像上通过采样器G构造两个子图（$g_1(y)，g_2(y)$），通过着两个子图构建重构损失函数(1.3推导)
2. 对原图进行推理降噪，得到的降噪图像再通过相同的采样方法得到两张子图，计算正则项

对于采样器G：设计了近邻采样，即将图像分为2*2的单元，再每个单元中随机选择两个紧邻像素分别划分到两个子图之中，这样构建处两个“相似但是不同”的子图。

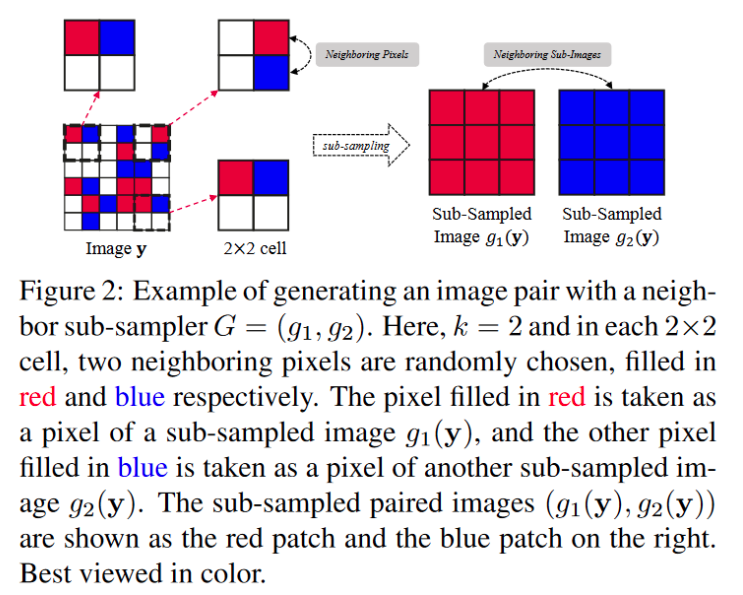
2. 实验结果

  分别测试了Gaussian和Poisson噪声，每种噪声分别尝试了固定噪声水平和动态噪声水平两种情况。结果表明，在多个测试集上，本方法在性能上比使用配对数据训练的方法（N2C）低0.3dB左右，超越了现有的自监督降噪方法。在动态噪声水平的场景下，显著超越其他自监督方法，甚至与自监督+后处理的Laine19不相上下。

消融实验说明正则化的有效性：当权重为0时，Neighbor2Neighbor退化为pseudo Noise2Noise，此时模型的PSNR/SSIM水平较低，而网络输出的图像过于模糊而损失了大部分的细节信息；随着权重增加，模型的PSNR/SSIM开始提高，此时降噪的图像开始保留更多的细节，但是噪声也被更多地保留下来。而当权重太大的时候，模型的PSNR/SSIM开始降低，而降噪图像也变得更加Noisy。由此可见，正则项起到了平衡降噪能力和细节保留的作用。针对不同的场景，选择合适的权重，可以发挥出Neighbor2Neighbor的最佳效果。

3. 总结

1. 提出了基于采样配对的 Noise2Noise去噪训练方法，使用添加正则化的方法消除不同采样之间的偏差（$ϵ$）
2. 采样的策略后续也被应用到 Blind2Unblid工作之中了
3. 强假设仍然存在，影响方法的泛化性
   • 噪声是零均值的