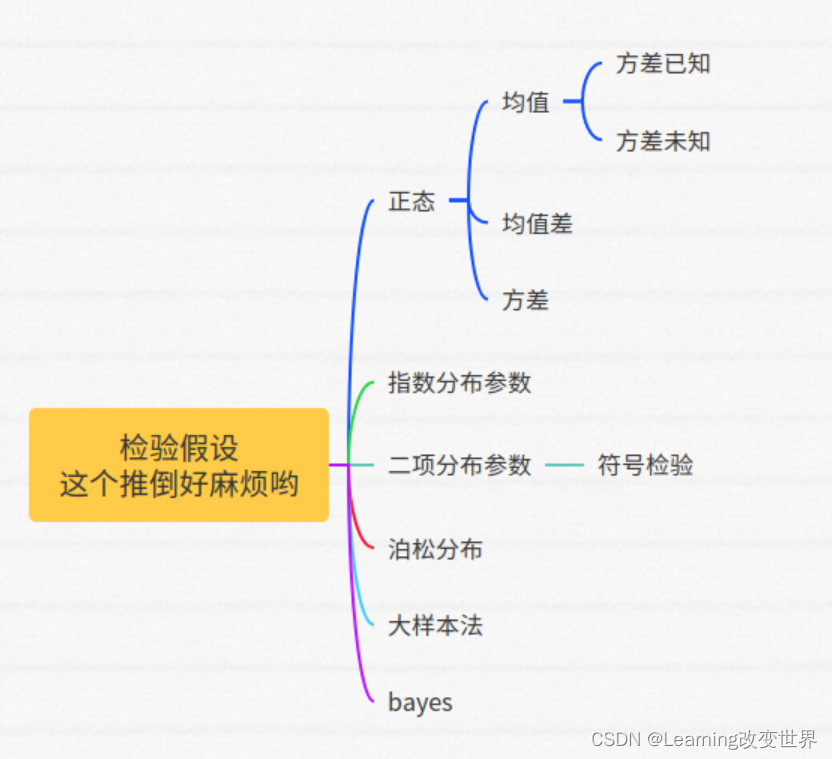
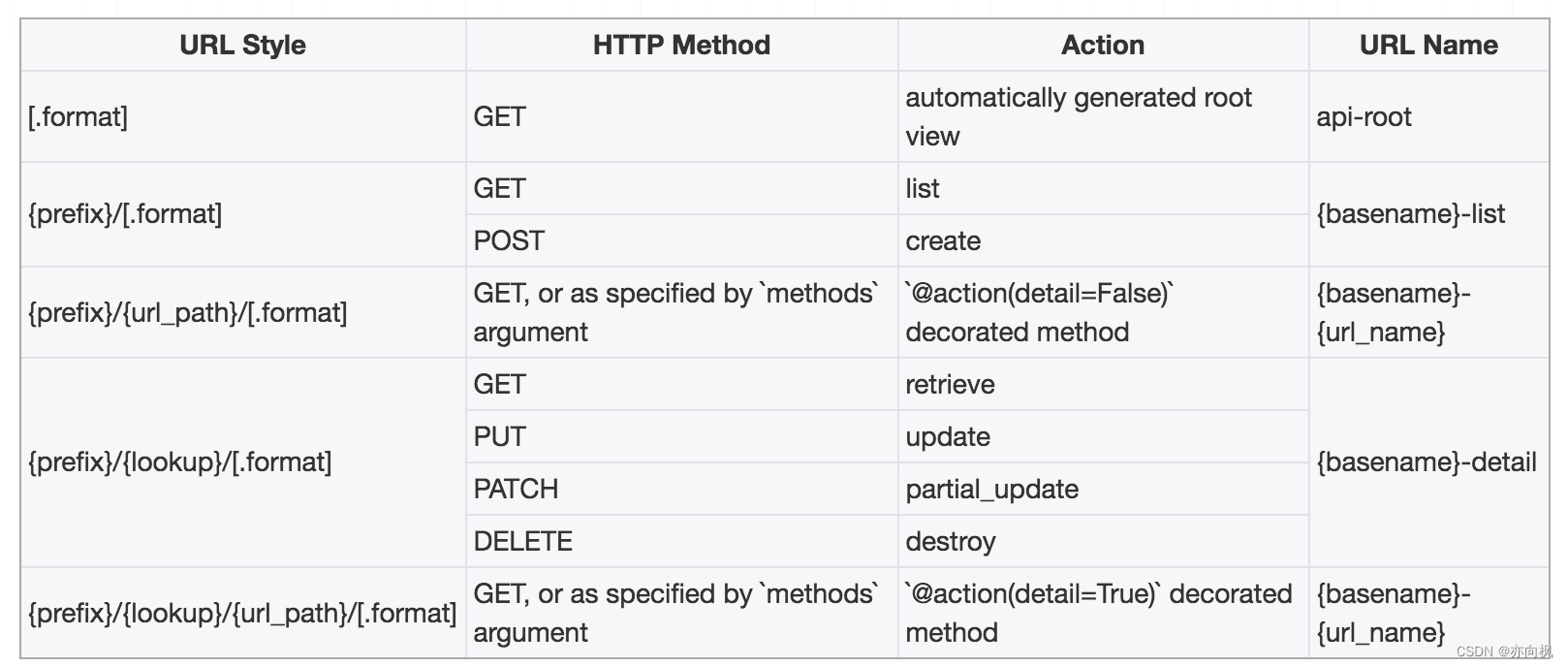
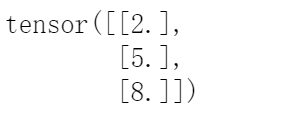文章截图来源来源B站：蚂蚁学python

 引入并发，就是为了提升程序运行速度

 1、基础介绍

 

1-1 CPU密集型计算、IO密集型计算

  1-2 多进程、多线程、多协程对比

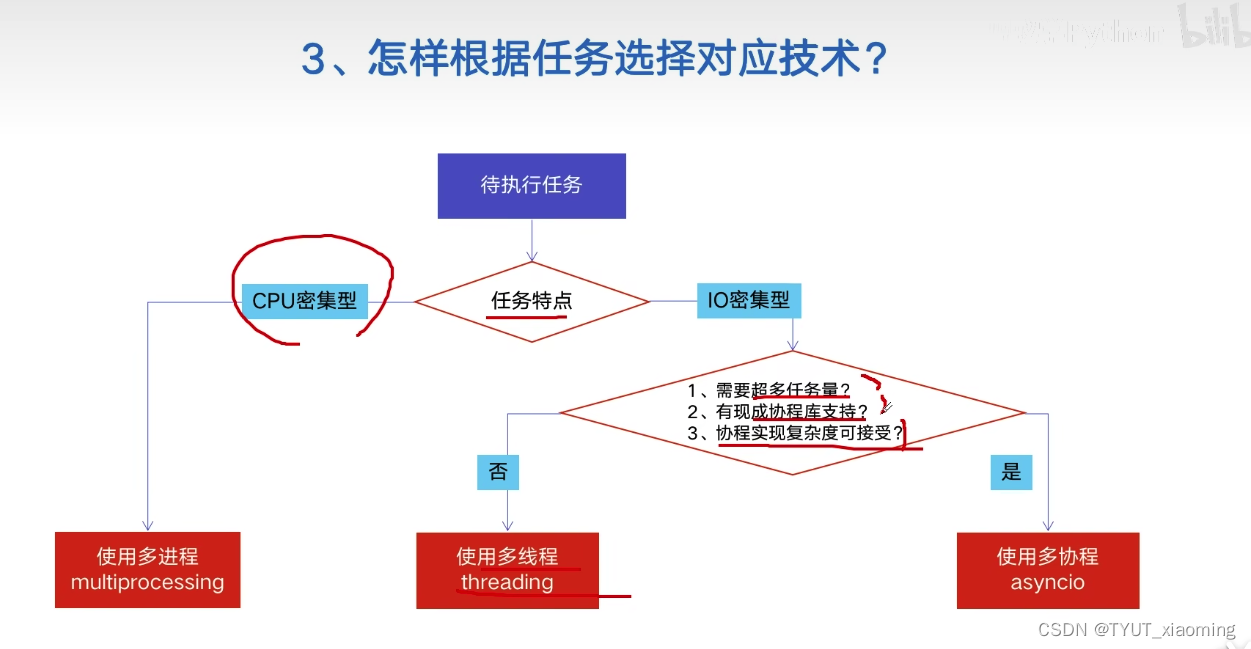
 2、全局解释器锁GIL

2-1 python速度慢的两大原因

2-2 GIL是什么

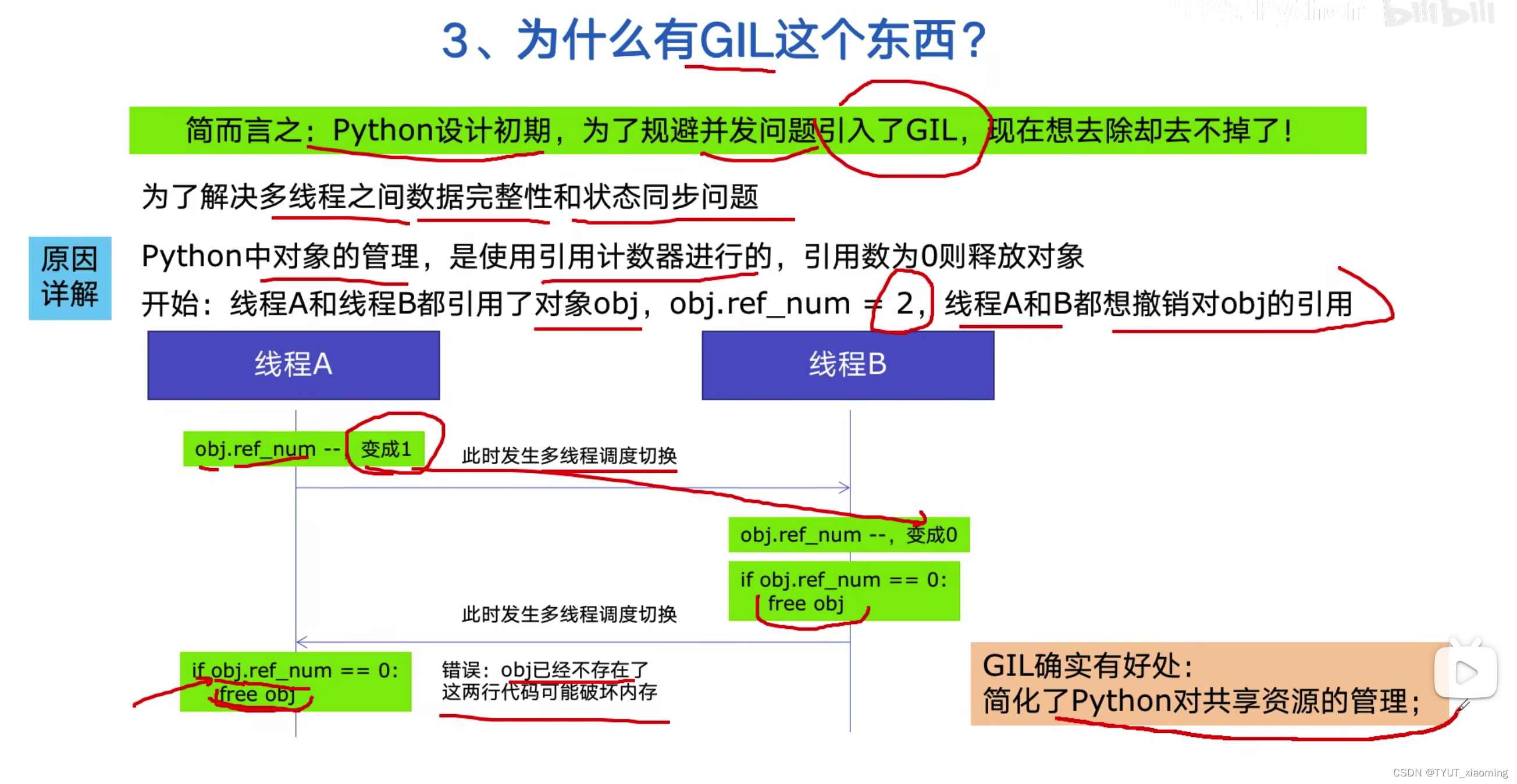
2-3 为什么有GIL这个东西

  

2-4 怎样规避GIL带来的限制

3实践

3-1python创建多线程的方法

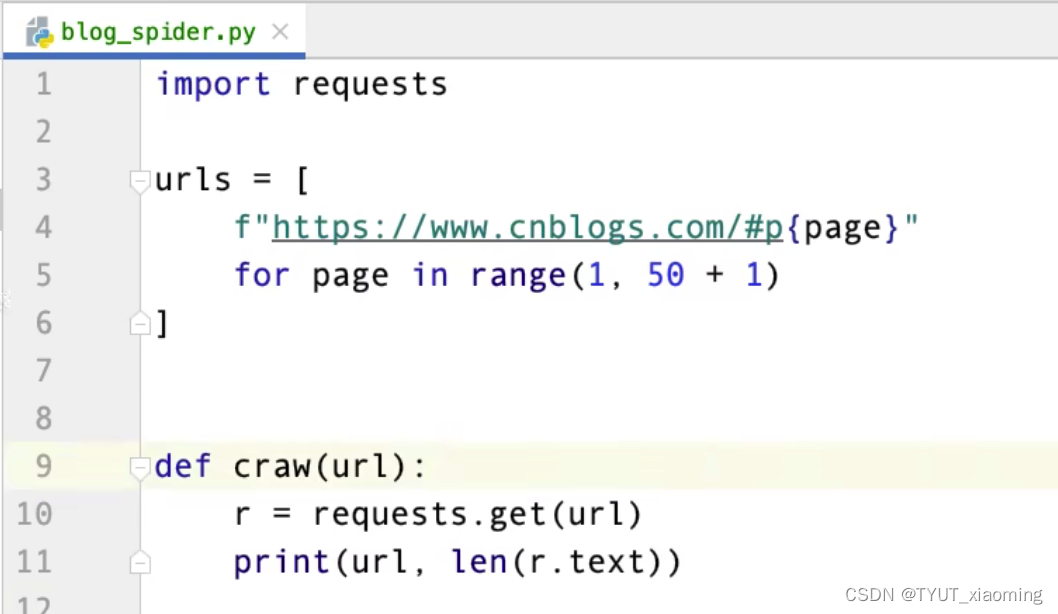
 3-2事件爬虫代码（单线程和多线程）

blog_spider.py代码

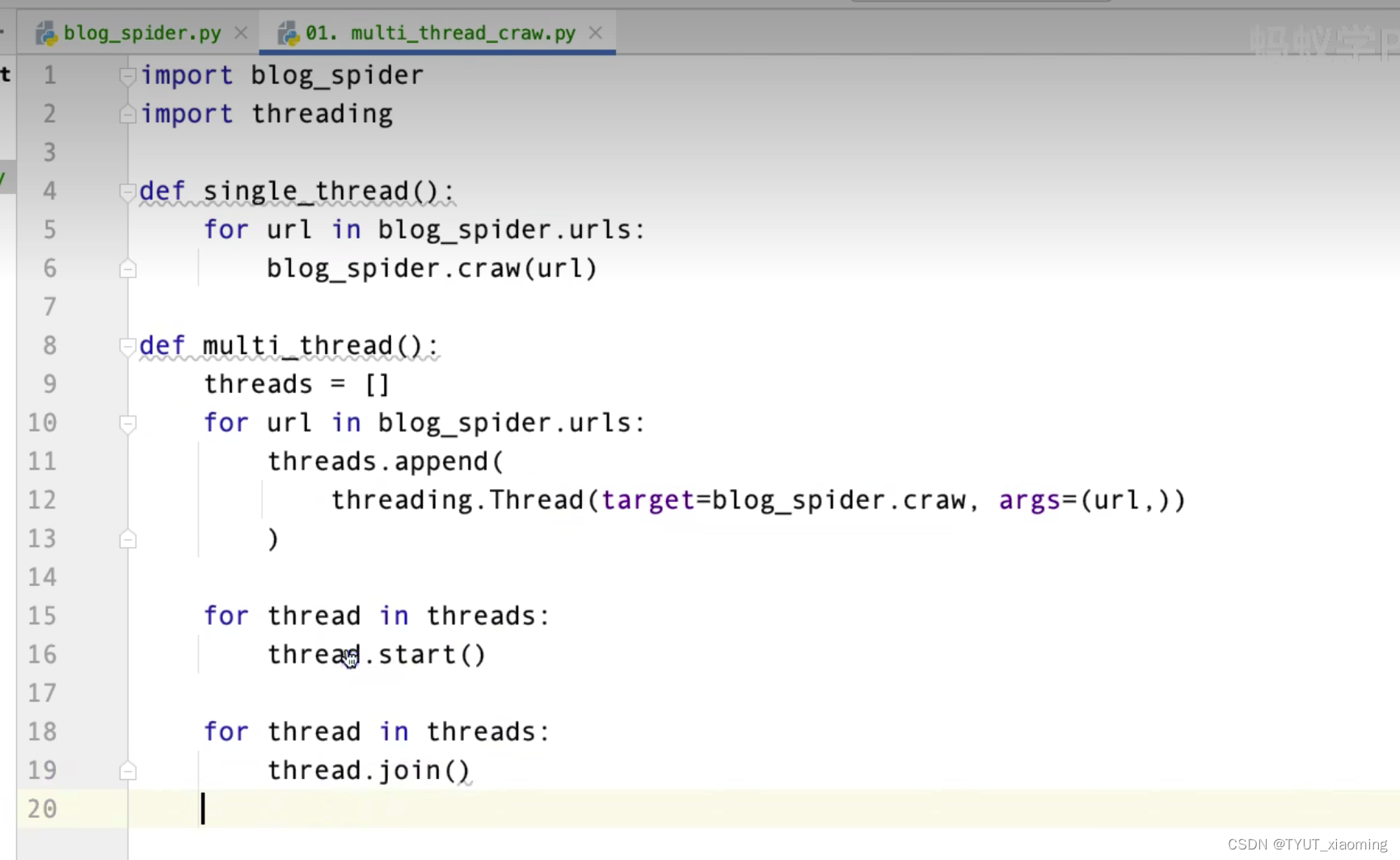
 muti_thread_craw.py代码