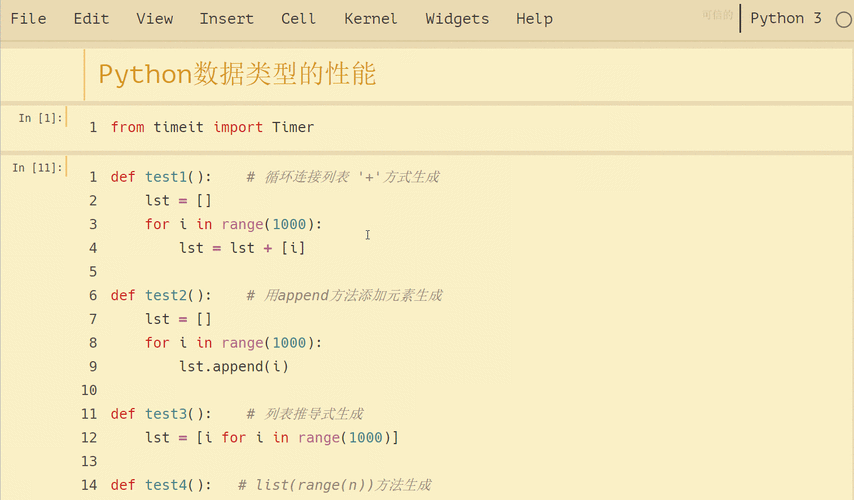
calculus
微积分教会我为什么椭圆的面积= π \pi πab.

隐函数求导Rule
如何理解Lagrange求函数极值?
万物可积(所有的函数都能找到原函数?)——数即宇宙
线性代数
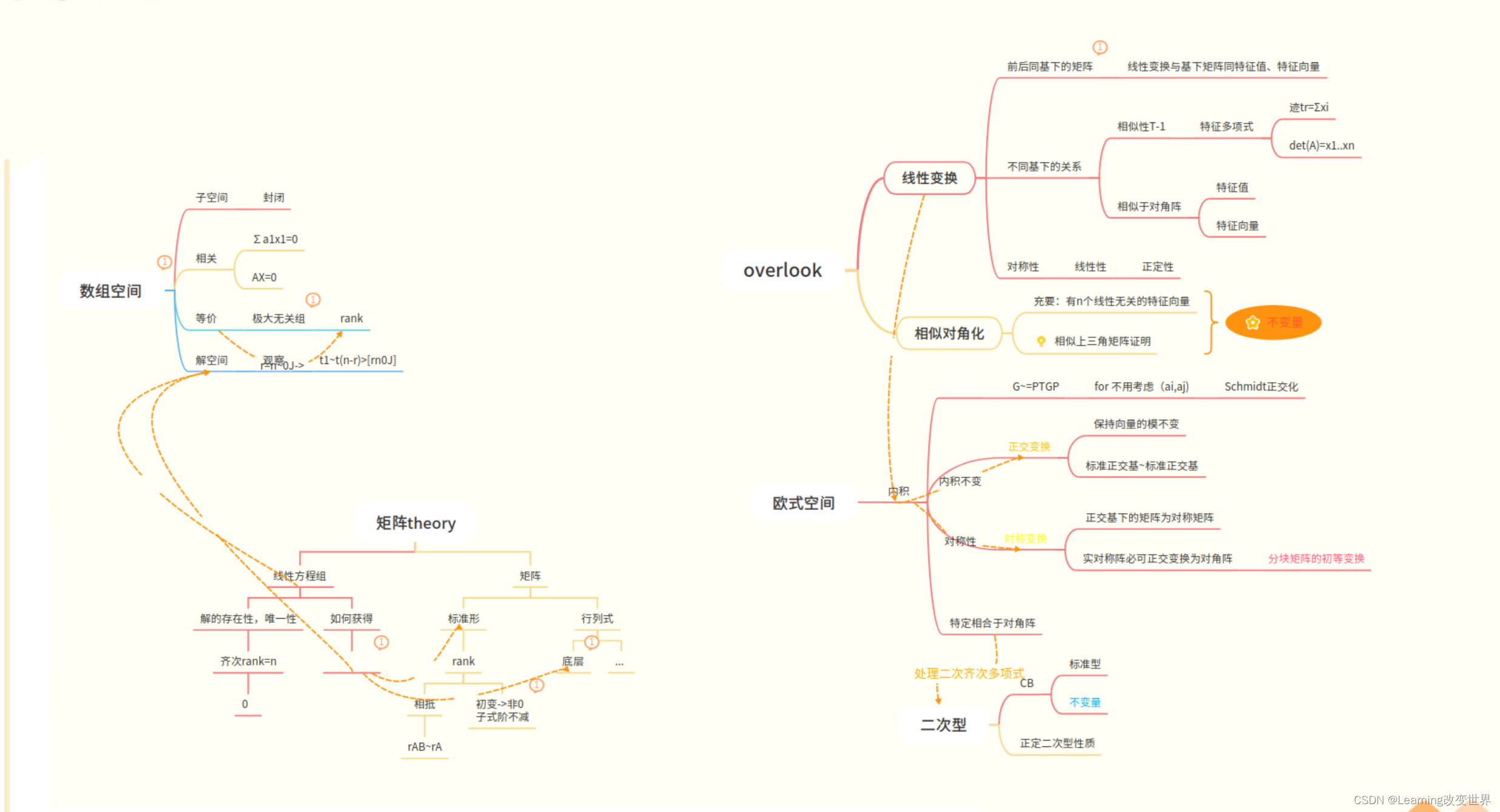
- It’s doubtless that Gitmind&Blog is best place for taking notes!
概率论
- 什么是负二项分布
- 三大分布变量的函数,均值,方差——本质是计算,要点是记忆(理解)
- 卡方分布,originate from τ \tau τ 函数—— τ ( x ) = ∫ 0 + ∞ e − t t x − 1 d t \tau(x)=\int_0^{+\infin} e^{-t}t^{x-1}dt τ(x)=∫0+∞e−ttx−1dt,prop1: τ ( x + 1 ) = x τ ( x ) \tau(x+1)=x\ \tau(x) τ(x+1)=x τ(x)
produce k n ( x ) = e − x / 2 x − ( n − 2 ) / 2 τ ( n / 2 ) 2 n / 2 k_n(x)=\frac{e^{-x/2}x^{-(n-2)/2}}{\tau(n/2)2^{n/2}} kn(x)=τ(n/2)2n/2e−x/2x−(n−2)/2,记为 x n 2 x_n^2 xn2,满足累加律,正态分布的平方和satisfies卡方分布
inclusion 1:Xi corresponds with index distribution,2 λ X i \lambda X_i λXi complies with x 2 2 x_2^2 x22
- 卡方分布随后produce T分布和F分布
- 正态分布是独立同分布变量和在n n → + ∞ n\rightarrow +\infin n→+∞的近似
数理统计

common pipeline:
- 给定变量分布,样本已知,估计参数(点估计)或判断参数(参数检验);
- 参数和变量分布已知(或 大样本法/beyas 强推),按照给定的概率估计样本区间(区间估计);
- 还可参数与样本已知下,判断变量分布 的置信度(拟合优度的检验)。
- 可见3个主元=变量分布,参数,样本
- 三大分布就是为了后面的区间估计和参数检验而生的
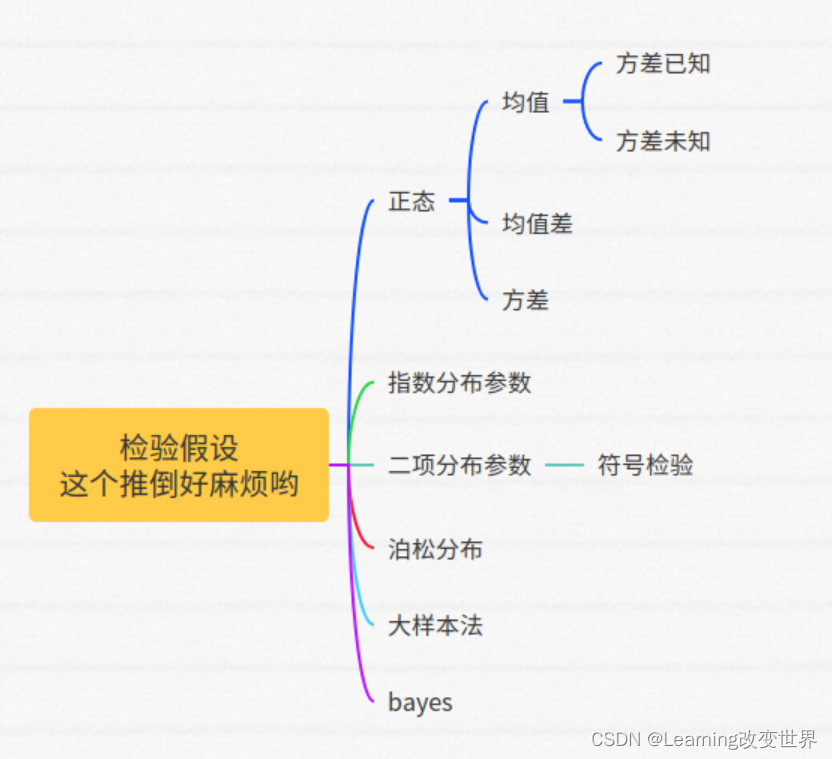
Process of(指定水平 α \alpha α 给出 对参数的假设的 检验):
给定样本 和假设(变量分布)
- 表示第一类错误概率(根据 给定的假设H 和 带球的检验( X ‾ ≥ C \overline X \geq C X≥C )
- 恒等变形为 样本函数,利用经典结论 ,对应到 三大统计的分布函数,
- 根据“有水平 α \alpha α”的定义,只要分布函数的最大值 ≤ α \leq \alpha ≤α,一元一次方程解出检验中的参数C