A - Round decimalsA - Round decimals

题目大意

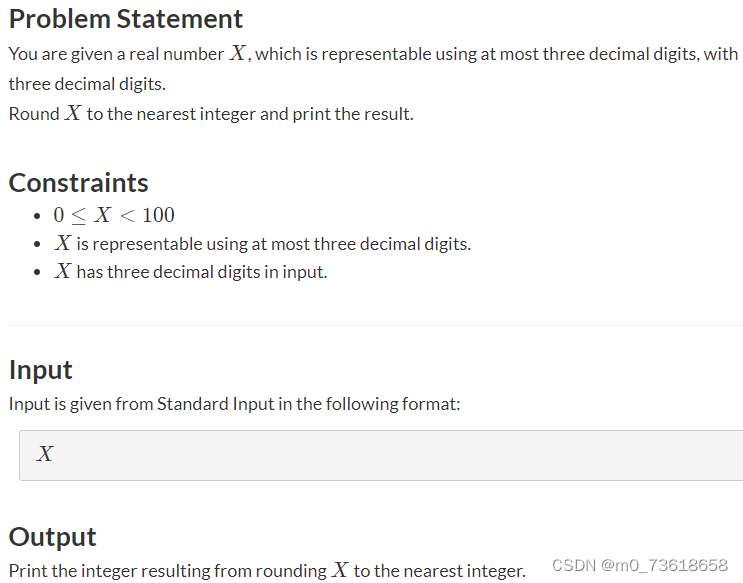
给定一个实数X，它最多可以使用三位小数表示，而且X的小数点后有三位小数。将X四舍五入到最接近的整数并打印结果。

思路分析

可以使用round函数进行四舍五入

知识点

round(x) 是一个用来对数字进行四舍五入的函数。它接受一个参数 x，可以是整数、浮点数或其他可转换为数字的对象。该函数会根据传入的值 x 进行四舍五入，并返回一个最接近 x 的整数。

具体的规则如下：

如果 x 是一个正数且小数部分大于等于 0.5，则 round(x) 返回大于 x 的最接近整数；
如果 x 是一个正数且小数部分小于 0.5，则 round(x) 返回小于 x 的最接近整数；
如果 x 是一个负数且小数部分绝对值大于等于 0.5，则 round(x) 返回小于 x 的最接近整数；
如果 x 是一个负数且小数部分绝对值小于 0.5，则 round(x) 返回大于 x 的最接近整数；
如果 x 是一个整数，则 round(x) 直接返回 x。

以下是一些例子：

round(3.2) 返回 3。
round(4.8) 返回 5。
round(-2.5) 返回 -2。
round(6) 返回 6。

时间复杂度

O(1)

AC代码

#include <iostream>
#include <cmath>
using namespace std;
int main() {
    double x;
    cin >> x;
    cout <<(int)(round(x)) << endl;
    return 0;
}

B - Counting ArraysB - Counting Arrays

题目大意

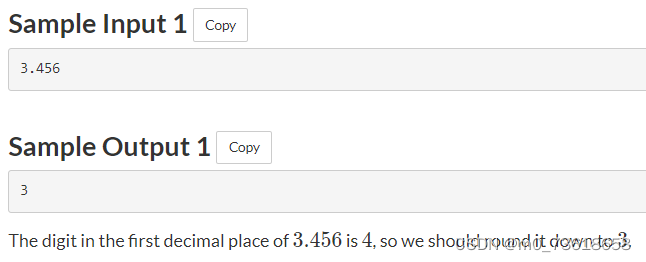
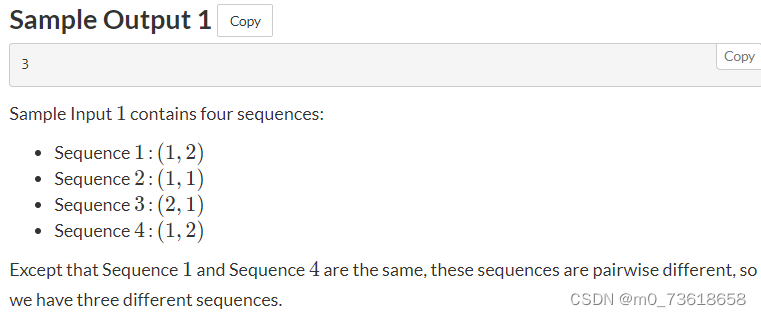
给定N个序列，每个序列的长度为Li，并且第i个序列的第j个元素为a_i,j。当且仅当序列i和序列j的长度相等且对应位置的元素相等时，认为序列i和序列j相同。求这N个序列中有多少个不同的序列。

思路分析

可以使用集合（set）来存储不同的序列。对于每一个序列，将其存储为一个vector，然后将该向量插入到set中。由于set会自动去重，所以最终set中存储的向量数量就是不同序列的数量。

时间复杂度

O(NMlogN)

AC代码

#include <iostream>
#include <set>
#include <vector>
using namespace std;

int main() {
  int N;
  cin >> N;
  set<vector<int>> st;
  for(int i = 0; i < N; i++) {
    int L;
    cin >> L;
    vector<int> v(L);
    for (auto& x : v) cin >> x;
    st.insert(v);
  }
  cout << st.size() << "\n";
}

C - Martial artistC - Martial artist

题目大意

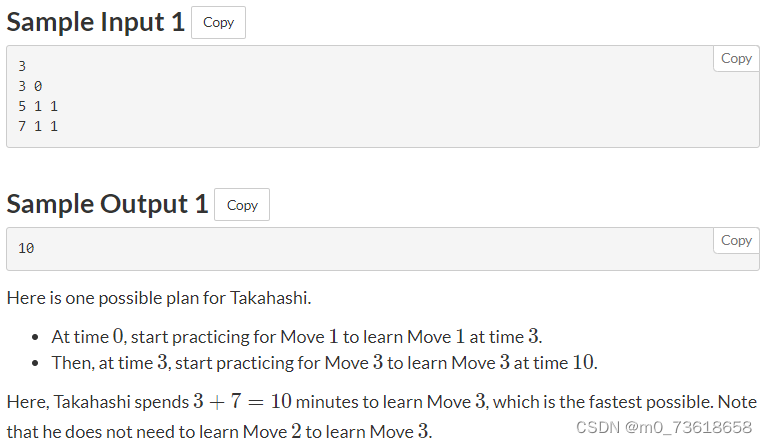
Takahashi是一位武术家。有N个他可以学习的招式，分别称为Move 1, Move 2, …, Move N。每个招式需要Ti分钟的练习时间才能学会。此外，在开始练习之前，必须已经学会所有的招式A[i][j]。其中，对于每个招式i，保证A[i][j] < i对于每个1 ≤ j ≤ Ki。
Takahashi在时间0时还没有学会任何招式。他不能同时练习多个招式，也不能停止已经开始的练习。找出Takahashi学会Move N所需的最少分钟数。

思路分析

贪心算法
针对每个招式i，如果已经学会了该招式的前置招式A[i][j]，那么就可以开始练习招式i，并且需要消耗Ti分钟的练习时间。使用一个bool数组used[N]来记录每个招式是否被使用过。

从最后一个招式N开始向前遍历，如果该招式已经被使用（即前面的招式都已经学会），则将其练习时间Ti加到答案ans上，同时将它所依赖的前置招式全部标记为已使用。
最后输出答案ans即为学会Move N所需的最少分钟数。

时间复杂度

O(N)

AC代码

#include <bits/stdc++.h>
using namespace std;
#define N 200100
#define ll long long
#define rep(i, n) for(int i = 0; i < n; ++i)

ll t[N]; // 存储每个招式的练习时间
int k[N]; // 存储每个招式的前置招式的数量
vector<int> e[N]; // 存储每个招式的前置招式的索引
bool used[N]; // 记录每个招式是否被使用过

int main(void) {
    int n, x;
    ll ans = 0;
    rep(i, N) used[i] = false;

    cin >> n;
    rep(i, n) {
        cin >> t[i];
        cin >> k[i];
        rep(j, k[i]) {
            cin >> x;
            e[i].push_back(x - 1);
        }
    }

    used[n - 1] = true;
    for (int i = n - 1; i >= 0; i--) {
        if (used[i]) {
            ans += t[i];
            rep(j, k[i]) {
                used[e[i][j]] = true;
            }
        }
    }

    cout << ans << endl;

    return 0;
}