算法思想比较

• 回溯法：有“通用解题法”之称，用它可以系统地搜索问题的所有解。回溯法是按照深度优先搜索(DFS)的策略，从根结点出发深度探索解空间树
• 分治法：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。步骤为分解、处理和解合并
• 动态规划：与分治法类似，将问题分解为子问题，但会找出最优子结构以避免大量重复计算，最后构造最优解

分治法、回溯法与动态规划的共同点：

• 都利用了子问题的解进行决策
• 都能利用递归的算法结构实现功能

1. 分治法、回溯法与动态规划是算法思想
2. 递归和迭代是算法结构
3. 算法思想使用算法结构实现功能

递归与回溯的区别

递归是一种算法结构。递归会出现在子程序中，形式上表现为直接或间接的自己调用自己。典型的例子是阶乘，计算规律为：$n!=n\ast (n-1)!$

int f(int n){
	return n == 1 ? 1 : n * f(n - 1);
}

回溯是一种算法思想，它有“通用解题法”之称，用它可以系统地搜索问题的所有解。回溯法是用递归实现的

分治法

分治法的设计思想：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

凡治众如治寡，分数是也。——孙子兵法

基本思想

分治法所能解决的问题一般具有以下几个特征：

1. 该问题的规模缩小到一定的程度就可以容易地解决
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
3. 利用该问题分解出的子问题的解可以合并为该问题的解
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题

回溯法

回溯法有“通用解题法”之称，用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。

在包含问题的所有解的解空间树中，按照深度优先搜索(DFS)的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。

若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

解题步骤

1. 针对所给问题，定义问题的解空间
2. 确定易于搜索的解空间结构
3. 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索

动态规划

动态规划（Dynamic Programming, DP）是一种解决多阶段决策过程最优化问题的数学方法。动态规划的特点是将原问题分解成多个子问题进行求解，每个子问题只求解一次，并将其结果保存下来，避免重复计算。然后通过组合子问题的解来得到原问题的解。

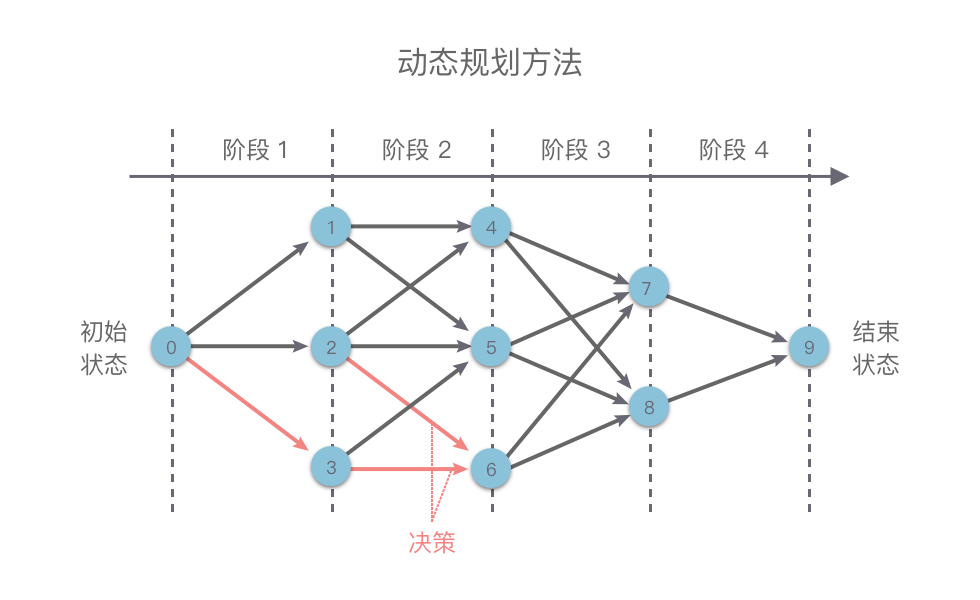
核心思想

动态规划一般用于求解具有重叠子问题和最优子结构的问题，例如最长公共子序列、背包问题、最短路径等。重叠子问题指的是在求解问题的过程中，多次用到相同的子问题，最优子结构指的是问题的最优解可以通过子问题的最优解来构造。

解题步骤

动态规划的基本步骤是：

1. 状态定义
2. 状态转移方程（最优子结构）
3. 边界条件
4. 最优解的计算

状态指的是子问题的描述信息，状态转移方程指的是子问题之间的关系，边界条件指的是最简单的子问题的解法，最优解的计算则是通过递推或者回溯等方式得到

---

参考资料：

1. Leetcode 回溯法详解
2. Leetcode 分治法详解
3. Leetcode 动态规划详解