树的重要性
二分查找算法、几种核心的排序算法以及图算法都与树有非常密切的关系。有句话锁,“没学会树,算法相当于白学”,可见,树在算法中的地位。
树的考察方面
层次遍历以及拓展问题
前后序遍历与拓展问题
中序遍历与搜索树问题
堆和平衡树等变换的树问题
重点
- 层次遍历:全部的层次遍历几乎就一个模板,本身也不难。本部分除了要掌握层次遍历的实现方法外,还要掌握相关的常见变题。
- 树的前中后序是面试的热点,其根基都是递归。需要掌握递归的原理和写法,掌握前中后序遍历的迭代和递归方法实现方法,掌握前序和后续相关的经典题目。这些内容也是后面回溯、动态规划等的基础
- 如果将二分查找的搜索画成树,那与二叉树的中序搜索完全一样。因此二叉树的中序遍历和搜索树的本质是一样的,需要理解其原理和几个常见的题目。
- 除此之外还有很多特殊结构的树:
- 平衡树:为了提高搜索树的效率而产生
- 红黑树:为了提高平衡树的效率而产生。而红黑树的本质就是2-3树。
- 堆也是一种非常重要的结构,有很多经典题目几乎只能用堆
树的常见概念
定义
树是一个有n个有限节点组成的一个具有层次关系的集合。每个节点有0个或多个子节点,没有父节点的节点称为根节点(一棵树有且只有一个)。
树的种类比较多,最常见的就是二叉树了。
二叉树的基本结构
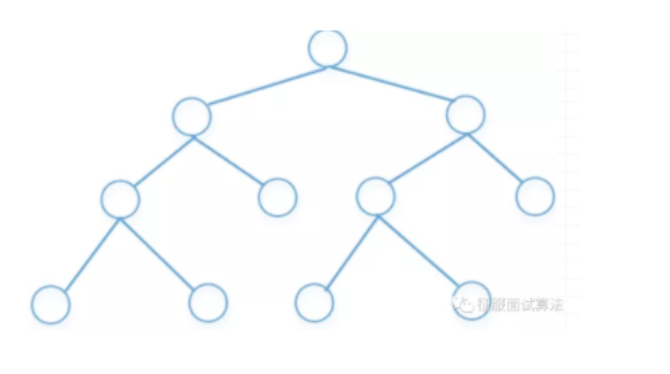
参考上面的结构,可以很方便的理解树的如下概念:
- 节点的度:一个节点含有的子节点的个数
- 树的度: 一棵树中,最大节点的度(注意与节点度的区别)
- 叶子结点(终端节点): 度为0的节点
- 非终端节点(分支节点): 度不为0的节点
- 双亲节点(父节点): 若一个节点含有子节点,则这个节点称为其子节点的父节点
- 子节点(孩子节点): 一个节点含有的子树的根节点称为该节点的子节点
- 兄弟节点: 具有相同父节点的节点互称为兄弟节点
- 节点的祖先:从根节点到该节点所经分支上的所有节点
- 子孙:以某节点为根的子树中任一节点 都称为该节点的子孙
- 森林:由m (吗>=0)棵 互补相交的树的集合
- 无序树:树中任意节点的子节点之间没有顺序关系
- 有序树:树中任意节点的子节点之间有顺序关系
- 二叉树: 每个节点最多含有两个子树的树称为二叉树
树的性质
性质1:在二叉树的第 i 层上,至多有2^(i-1)个节点(i > 0)
性质2:深度为k 的二叉树至多有 2^k - 1个节点(k > 0)
性质3:对于任意一棵二叉树,如果其叶子结点数为N0,而度为2的节点总数为N2,则N0=N2+1
性质4: 具有n个节点的完全二叉树的深度必为log2(n+1)
性质5: 对于完全二叉树,若从上至下,从左至右编号,则编号为i的节点,其左孩子编号必为2i,右孩子编号必为 2i+1,其双亲编号必为 i / 2 (i = 1时 为根 除外)
满二叉树和完全二叉树的区别
满二叉树
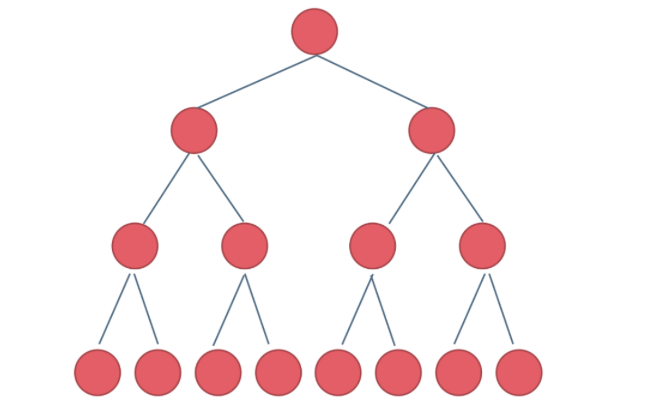
如果一棵树只有度为0 的节点和度为2 的节点,并且度为0 的节点在同一层上,则这棵树称为满二叉树
完全二叉树
在完全二叉树中,除了最底层节点可能没有填满外,其余每层节点数都达到最大值。并且最下面一层的节点都集中在最左边的若干位置。
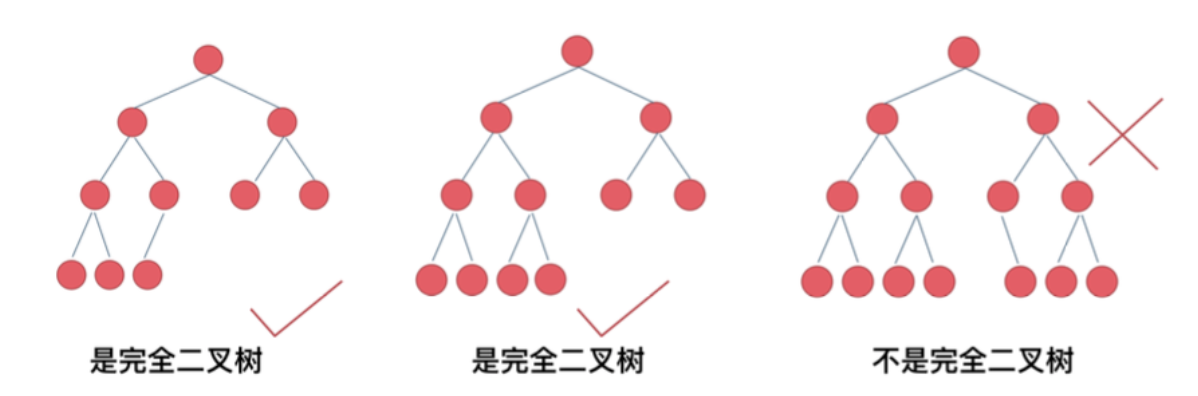
前面两棵树的前n-1层都是满的,最后一层所有节点都集中在左侧区域,二节点之间不能有空隙。最后一棵树有一个节点缺少了左节点,因此不是完全二叉树。
树的构建
二叉树定义
public class TreeNode{
int val;
TreeNode left;
TreeNode right;
}解释:
这里本质上就两个引用,分别指向两个位置,为了便于理解,分别命名为左、右孩子
定义N叉树
public class TreeNode{
int val;
List<TreeNode> nodes;
}树的存储方式
数组
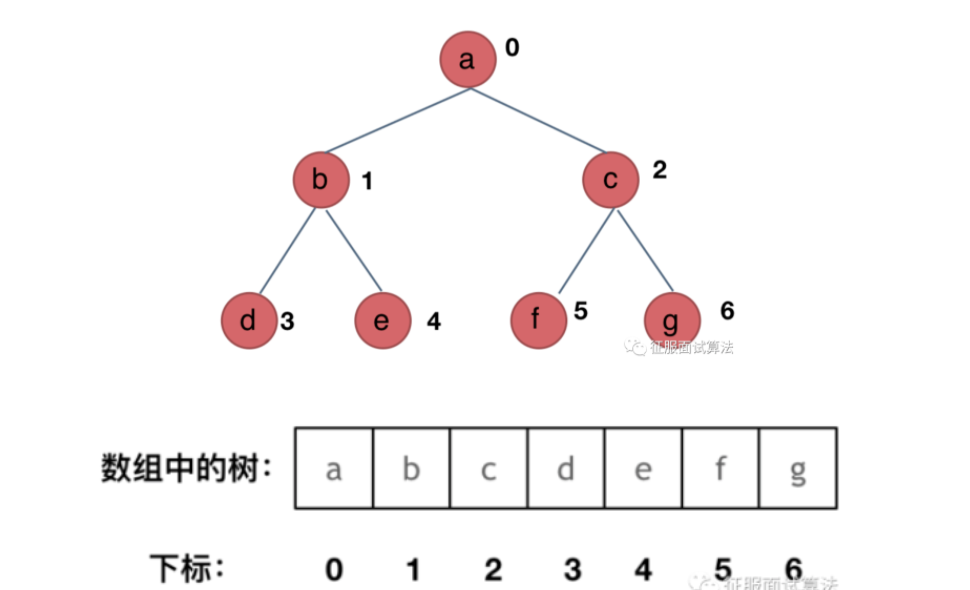
遍历问题:
由于数组的下标是从0开始的。因此与之前说的编号有一点点不同。如果父节点的数组下标是i,name它的左孩子就是i * 2 + 1,右孩子是 i * 2 + 2。
缺点
可能存在大量的控件浪费。
链表
能更好地表示树的结构,因此一般都用链表的方式来表示树。
树的遍历方式
- 深度优先遍历:先往深走,遇到叶子节点再往回走
- 广度优先遍历:一层一层的遍历,一层遍历完再访问下一层
这两种遍历方式不仅适用于二叉树,N叉树、图结构等适用。
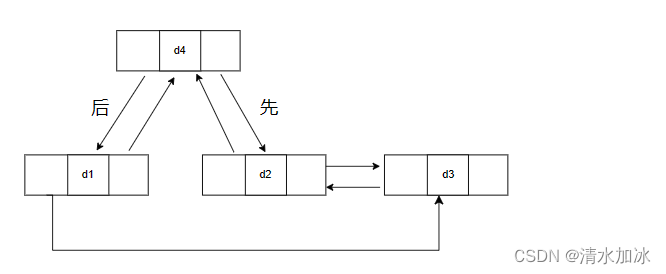
深度优先又有前中后序三种遍历方式,区分其中的关键就是中间父节点的位置:
前 指的是中间父节点在遍历中的顺序在 前面
前中后序指的就是中间节点的位置
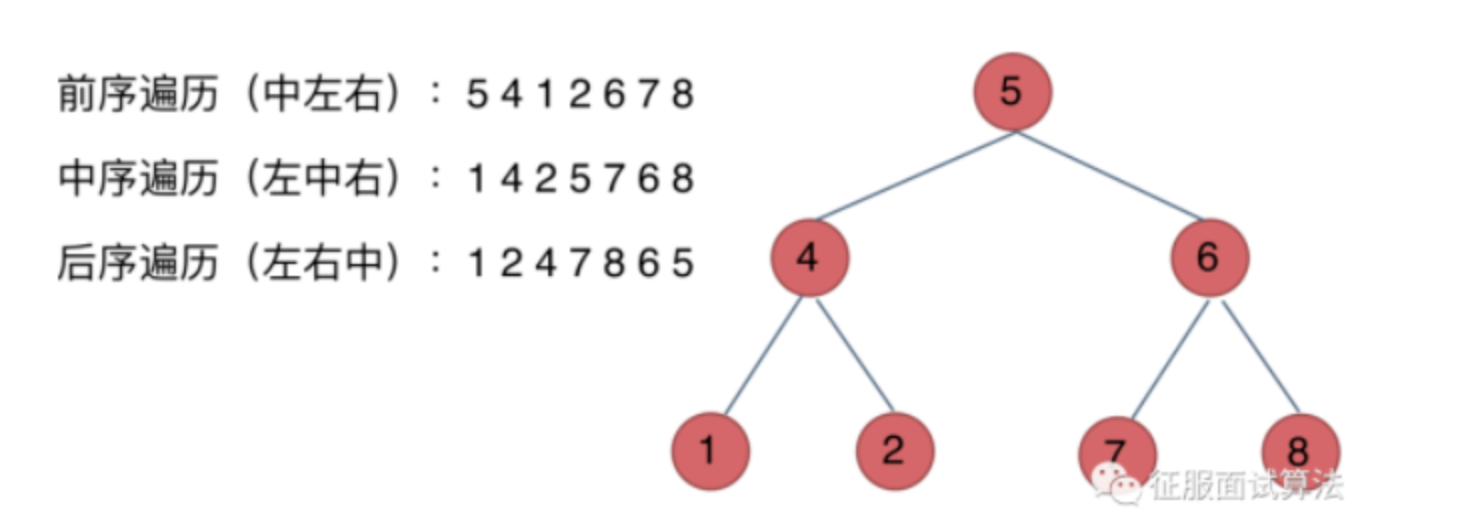
遍历顺序
访问中间节点的顺序就是所谓的遍历顺序:
前序遍历:中左右
中序遍历:左中右
后续遍历:左右中
图例