# 游游的字母变换
题目大意
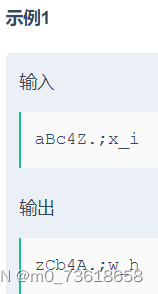
对给定的字符串进行变换,将大写字母变为下一个字母,小写字母变为上一个字母,其他字符不做变换。
思路分析
- 如果字符是大写字母,则判断是否为’Z’,如果是则变为’A’,否则将其加1。
- 如果字符是小写字母,则判断是否为’a’,如果是则变为’z’,否则将其减1。
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;
cin>>s;
for(int i=0;i<s.size();i++)
{
if(isupper(s[i])){
s[i]=s[i]=='Z'?'A':s[i]+1;
}else if(islower(s[i])){
s[i]=s[i]=='a'?'z':s[i]-1;
}
}
cout<<s<<endl;
return 0;
}
游游的排列构造
题目大意
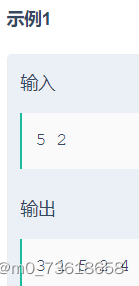
构造一个长度为n的排列,其中有k个"好元素",并且任意两个好元素都不相邻。好元素的定义是,对于第i个元素a[i]而言,a[i]是前i个元素的最大值。
思路分析
先将最大的k个数按间隔和顺序放置在数组中。
然后,将剩下的数按顺序填充到数组的空位中。
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,k;
cin>>n>>k;
vector<int> a(n);
int x=n-k+1; // 第一个好元素的值
for(int i=0;i<k;i++){
a[2*i] =x;
x++;
}
int cnt = 1;
// 填充其他位置
for(int i=0;i<n;i++){
if(a[i]==0){
a[i] =cnt;
cnt++;
}
}
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
return 0;
}
游游的二进制树
题目大意
题目给出了一棵树,每个节点有一个权值为0或者1。路径表示二进制数。现在需要计算有多少条路径代表的二进制数在[l,r]区间范围内。
思路分析
可以使用深度优先搜索(DFS)来解决这个问题。从根节点开始遍历树的每一条路径,并将路径上的节点权值拼接起来得到对应的二进制数。如果该二进制数在[l,r]范围内,则计数器加1。
- 定义dfs函数,参数包括当前节点编号u,父节点编号fa,当前路径代表的二进制数mid。
- 将当前节点的权值加入mid中,并判断mid是否大于r,若是则退出递归。
- 如果父节点存在且mid大于等于l,则将计数器ans加1。
- 遍历当前节点的所有相邻节点v,若v不等于父节点fa,则递归调用dfs(v, u, mid)。
- 在主函数中,遍历所有节点,以每个节点作为起点调用dfs函数。
时间复杂度
O(n2)
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
vector<long long> a[N];
string s;
long long n, l, r, ans;
//深度优先搜索函数
void dfs(int u, int fa, long long x)
{
x= x * 2 + s[u - 1] - '0'; // 每次加上该点位的权值
if (x> r) return; //如果x大于r,则退出
if (fa && x>= l) ans++; //如果fa不为0且mid大于等于l,则ans加一
for (int v : a[u])
{
if (fa == v) continue; //如果fa等于v,则跳过当前循环
dfs(v, u, x);
}
}
int main()
{
cin >> n >> l >> r >> s;
for (int i = 1; i < n; i++)
{
int x, y;
cin >> x >> y;
a[x].push_back(y);
a[y].push_back(x);
}
for (int i = 1; i <= n; i++)
dfs(i, 0, 0);
cout << ans << endl;
}