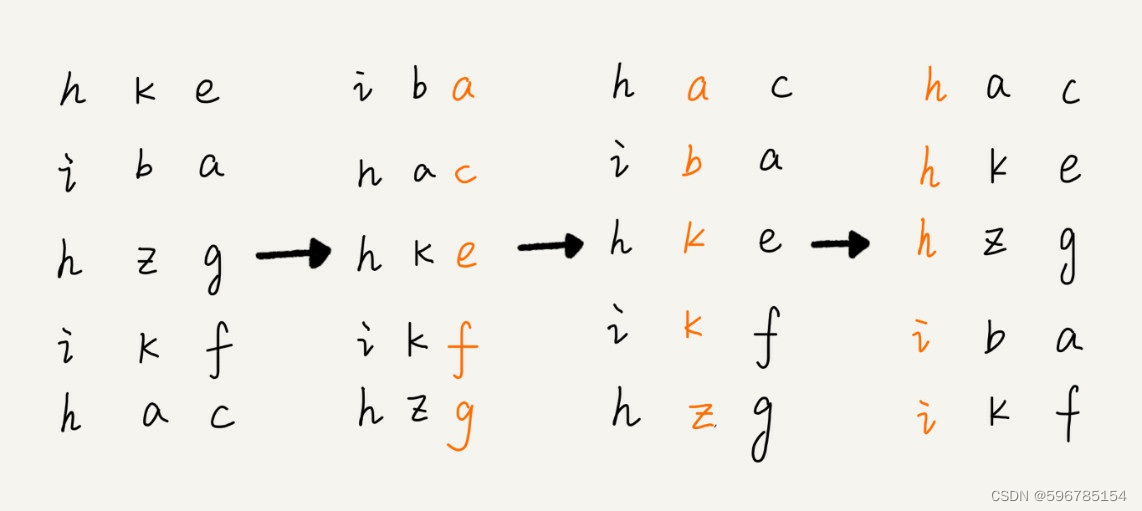题目描述：48. 旋转图像（中等）

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

LeetCode做题链接：LeetCode-旋转图像

示例 1：
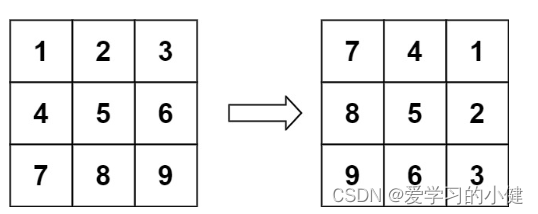
在这里插入图片描述

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：
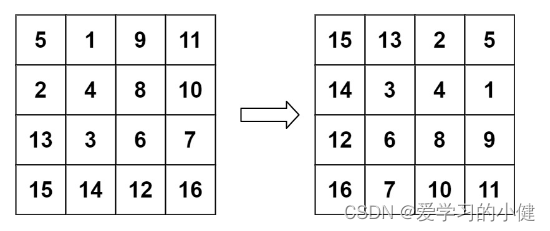
在这里插入图片描述

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

题目接口

class Solution {
    public void rotate(int[][] matrix) {

    }
}

解题思路

由于必须采用原地数组的方法，可以使用分层偏移，也就是一圈一圈的去圈子，每一圈中，偏移完一个元素后，偏移量+1
参考题解：逐层平移和偏移量的增加
先设定两个值：
比如第一圈的第一偏移，可以记录一个偏移量add = 0，第一次就是+0
在这里插入图片描述
第一圈的第二次偏移，add+1

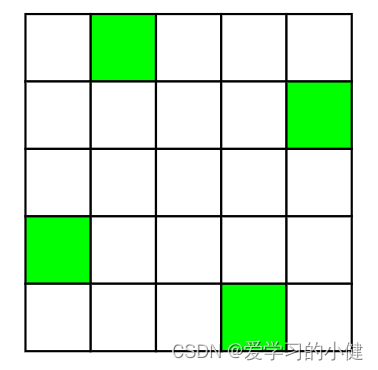
可以看出，第二次旋转的时候比第一次旋转偏移了一格，假设写出左上角的坐标为(pos1,pos1),右上角的坐标为(pos1,pos2),左下角的坐标为(pos2,pos1),右下角的坐标为(pos2,pos2),则能够写出偏移之后对应的坐标
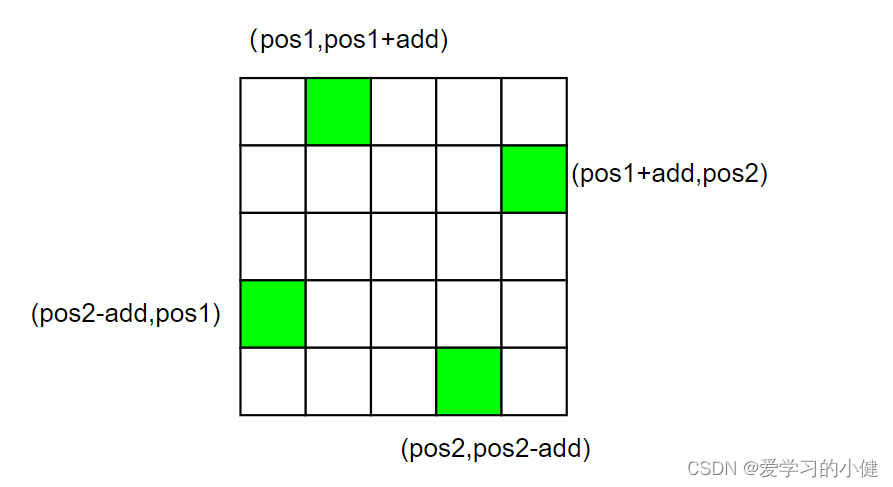
在这里插入图片描述
以此类推
然后偏移完后向内收缩一圈

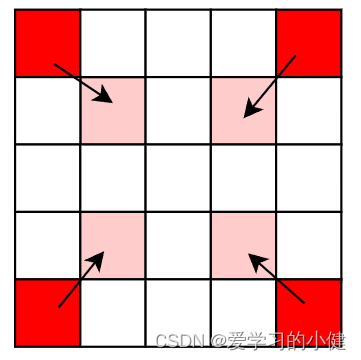
pos1 = pos1+1,pos2 = pos2-1,终止的条件为pos1 < pos2

代码

class Solution {
    public void rotate(int[][] matrix) {
		// 偏移量
        int add;
        // 中间变量
        int tmp;
        int pos1 = 0;
        int pos2 = matrix.length - 1;
        while (pos1 < pos2) {
            add = 0;
            // 一开始的最外围的一圈，然后逐渐往里面缩小
            while (add < pos2 - pos1) {
                // 四个点的旋转互换
                tmp = matrix[pos1][pos1 + add]; // 每一圈都会从圈的第一个点开始，比如：[0][0]、[1][1]、[2][2]
                matrix[pos1][pos1 + add] = matrix[pos2 - add][pos1];
                matrix[pos2 - add][pos1] = matrix[pos2][pos2 - add];
                matrix[pos2][pos2 - add] = matrix[pos1 + add][pos2];
                matrix[pos1 + add][pos2] = tmp;
                // 偏移量+1
                add++;
            }
            
            pos1++;
            pos2--;
        }
    }
}