通过序列构造二叉树
给出以下三个二叉树遍历的序列:
(1) 前序: 1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序: 8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
前中序复原二叉树
所需序列
(1) 前序: 1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2) 中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
左子树复原
第一轮
通过前序: 前序第一个访问的是根节点,因此根节点就是1
通过中序:中序遍历的特点就是根节点的左子树的元素都在根节点的左侧,右子树的元素都在根节点的右侧,从中序遍历序列结合前序序列可知,中序序列1的左侧为左子树,1的右侧为右子树。从而前序通过中序划分可知,前序的左右子树。划分如下:
中序序列划分: [3 4 8 6 7 5 2] 1 [ 10 9 11 15 13 14 12]
前序序列划分: 1 [2 3 4 5 6 8 7 ] [9 10 11 12 13 15 14]
分析
如何知道两个括号从哪里分开?可参照中序的两个数组划分的。
前序中 7 之前的元素都在中序第一个数组中,9之后的所有元素都在第二个数组中,因此从7和9之间划分。
第一轮划分结果如下图
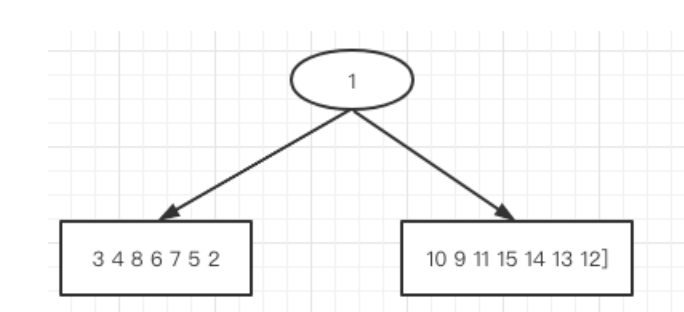
第二轮
我们先看前序和中序的第一个数组
前序: 2 3 4 5 6 8 7中序: 3 4 8 6 7 5 2
通过上面的结论可知:
根节点为2(前序)
然后可划分为:
前序: 2 [3 4 5 6 8 7 ]
中序: [3 4 8 6 7 5 ] 2
第二轮划分结果如下图
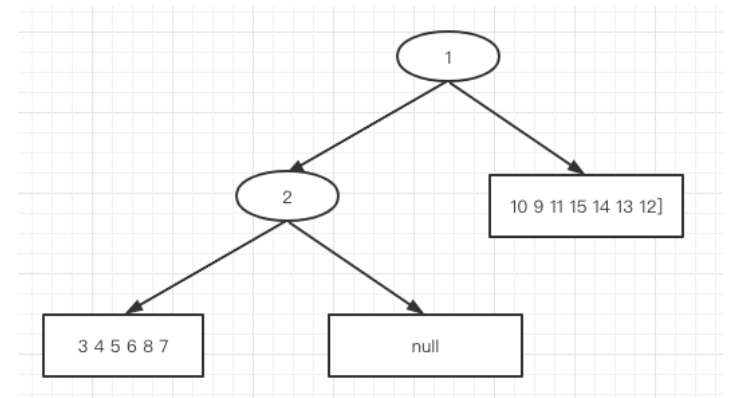
第三轮
对 3 4 5 6 8 7 继续划分:
前序: 3 [4 5 6 8 7]
中序: 3 [4 8 6 7 5]
第三轮划分结果如下图
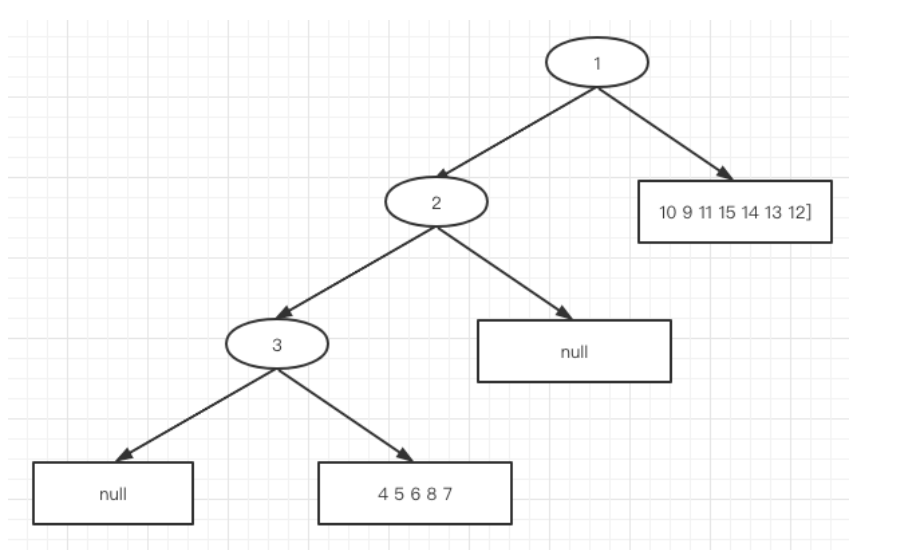
第四轮
对 4 5 6 8 7 进行划分:
前序:4 [5 6 8 7]
中序:4 [ 8 6 7 5 ]
第四轮划分结果如下图
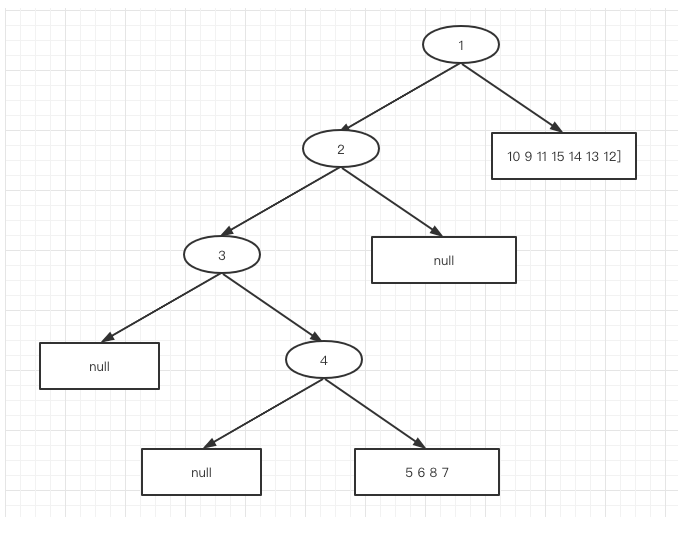
第五轮
对 5 6 8 7 划分:
前序:5 [6 8 7]
中序:[8 6 7] 5
第六轮
对 6 8 7 划分
前序:6 [ 8 7 ]
中序: [8] 6 [7]
至此,便可知左子树的树结构了。
左子树的树结构效果如下:
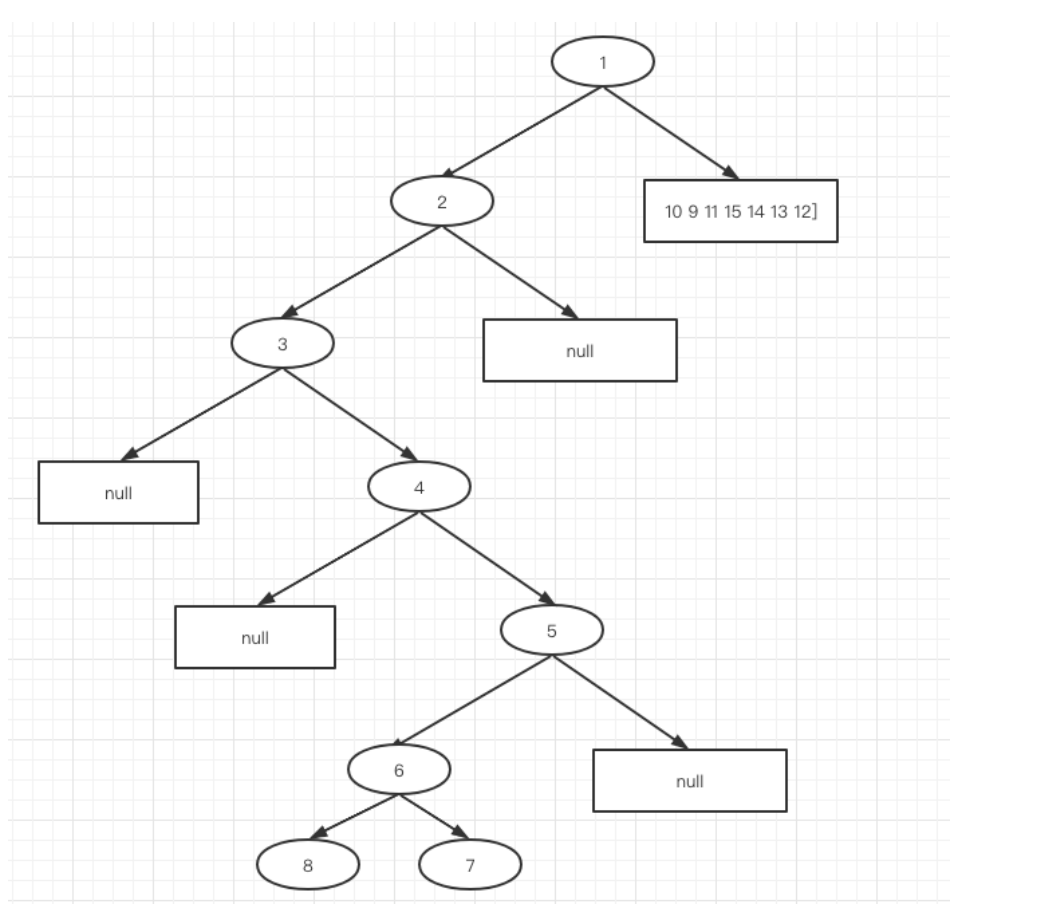
左子树的复原结果如下
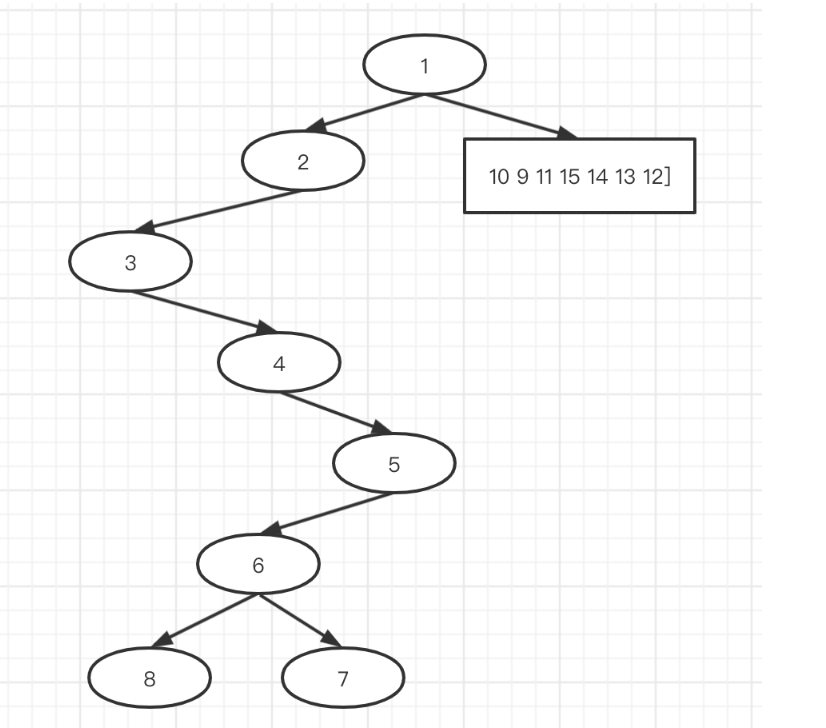
右子树复原
第一轮
由第一轮可知如下序列
前序: 9 10 11 12 13 15 14
中序: 10 9 11 15 13 14 12
对其进行划分,结果如下
前序:9 [ 10 11 12 13 15 14]
中序:[10] 9 [11 15 13 14 12]
由结果可知,10 是 9 的左子树,11 15 13 14 12为还需划分的序列
第二轮
将序列11 12 13 15 14进行划分:
前序:11 [12 13 15 14]
中序:11 [15 13 14 12]
第三轮
将12 13 15 14进行划分:
前序:12[13 15 14]
中序: [15 13 14]12
第四轮
将 13 15 14进行划分:
前序:13 [ 15 14]
中序: [15] 13 [14]
最终由中序获得结果,15为13的左子树,14为13的右子树
左右子树复原结果如下
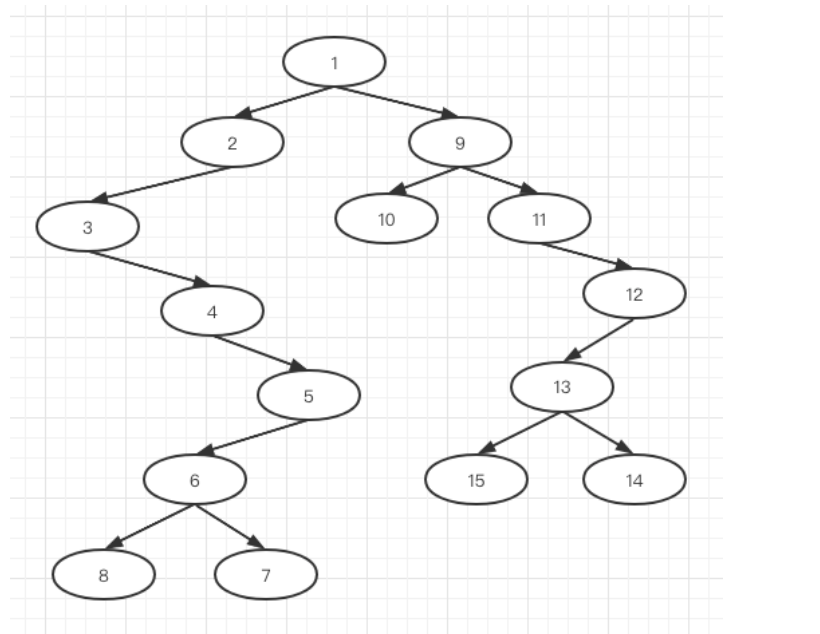
中后序恢复二叉树
通过中后序恢复二叉树与前中序唯一的不同就是:后续的最后一个是根节点,中序的处理和上述相同。所需序列如下:
(2) 中序: 3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序: 8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
左子树复原
第一轮
中序序列划分:[3 4 8 6 7 5 2] 1 [10 9 11 15 13 14 12]
后序序列划分:[8 7 6 5 4 3 2 ] [10 15 14 13 12 11 9 ]1
由于上述经过了上述分析,对划分结果有所了解了,因此此次划分就不画中间过程了
第二轮
对序列 8 7 6 5 4 3 2 进行划分
中序:[3 4 8 6 7 5 ] 2
后序:[8 7 6 5 4 3 ] 2
第三轮
对序列 8 7 6 5 4 3 进行划分:
中序:3[4 8 6 7 5]
后序:[8 7 6 5 4] 3
第四轮
对序列8 7 6 5 4进行划分:
中序:4 [8 6 7 5]
后序:[8 7 6 5] 4
第五轮
对序列8 7 6 5进行划分:
中序:[8 6 7 ] 5
后序:[8 7 6 ] 5
第六轮
对序列 8 7 6进行划分:
中序:[8] 6 [7]
后序:[8 7] 6
最终,由中序划分可知,8是6的左子树,7是6的右子树
左子树复原结果如下

右子树复原
右子树复原所需要的序列:
中序:10 9 11 15 13 14 12
后序:10 15 14 13 12 11 9
第一轮
将序列10 15 14 13 12 11 9进行划分(一般选择能确定根节点的那个节点):
中序:[10] 9 [11 15 13 14 12]
后序:[10 15 14 13 12 11] 9
由此划分可知,10为9的左节点,11 15 13 14 12为9的右子树
第二轮
对序列15 14 13 12 11进行划分:
中序:11 [15 13 14 12]
后序:[15 14 13 12] 11
第三轮
对序列15 14 13 12进行划分:
中序:[15 13 14] 12
后序:[15 14 13] 12
第四轮
对序列15 14 13 进行划分:
中序:[15] 13 [14]
后序:[15 14]13
从中序结果可知,15为13的左子树,14为13的右子树
左右子树复原结果如下

由此可知,前中序和中后序恢复成 二叉树的过程有些不同,但是所需的步骤和结果都是一致的。
知道了序列是如何构造成二叉树之后,便可以将其使用代码实现了,代码实现在下次总结。




![高级语言相关理论[编译VS解释,动态VS静态,强类型VS弱类型]](https://img-blog.csdnimg.cn/b773453c43934bdda431c03434a1cd7e.png)