1.桶排序

桶排序，顾名思义，会用到“桶”，核心思想是将要排序的数据分到几个有
序的桶里，每个桶内的数据再单独进行排序。桶内排完序之后，再把每个桶内的数据按照顺序依次
取出，组成的序列就是有序的了。

桶排序对要排序数据的要求是非常苛刻的。
首先，要排序的数据需要很容易就能划分成m个桶，并且，桶与桶之间有着天然的大小顺序。这样
每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。

其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶内的数据非常
多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果
数据都被划分到一个桶内，那就退化为O(nlogn)的排序算法了。

桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内
存有限，无法将数据全部加载到内存中。

/**
 * 桶排序
 * 原地排序：否
 * 稳定排序：是
 * 空间复杂度：
 * 时间复杂度：O(n)
 */
public class BucketSort {
	public static void main(String[] args) {
		int[] arr = { 1, 45, 32, 23, 22, 31, 47, 24, 4, 15 };
		bucketSort(arr);
		System.out.println(Arrays.toString(arr));
	}
	
	//存数区间0-9,10-19,20-29,30-39,40-49
	public static void bucketSort(int[] arr) {
		ArrayList bucket[] = new ArrayList[5];
		
		//初始化桶
		for(int i=0;i<bucket.length;i++) {
			bucket[i] = new ArrayList<Integer>();
		}
		
		//像桶内放入数据
		for(int i=0;i<arr.length;i++) {
			int index = arr[i]/10;
			bucket[index].add(arr[i]);
		}
		
		int index = 0;
		for(int i=0;i<bucket.length;i++) {
			bucket[i].sort(null);//对每个桶进行排序
			for(int j=0;j<bucket[i].size();j++) {
				arr[index++] = (int) bucket[i].get(j);
			}
		}
	}
}

2.计数排序

计数排序可以理解为是桶排序的一种特殊情况。当要排序的n个数据，所处的范围并不大的
时候，比如最大值是k，我们就可以把数据划分成k个桶。每个桶内的数据值都是相同的，省掉了桶
内排序的时间。

计数排序只能用在数据范围不大的场景中，如果数据范围k比要排序的数据n大很多，
就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，
要将其在不改变相对大小的情况下，转化为非负整数。
假定有原始数组A[8]，它们分别是：2，5，3，0，2，3，0，3。数据范围从0-5

先用一个数组大小为6的数组C来存储在k值上数据有几个。

接着对数组顺序求和，C数组存储的数据就变成了，C[k]里存储小于等于分数k的的数据。

定义临时数组R,依次扫描数组原始数组A，将数据A入到R[C[k]]位置上，同时C[k]位置上的数据要减掉1，最后将R数组复制到原始数组A中。

/**
 * 计数排序
 * 原地排序：否
 * 稳定排序：是
 * 空间复杂度：O(k+n) k为数据范围大小
 * 时间复杂度：O(n+k)
 */
public class CountSort {
	public static void main(String[] args) {
		int[] arr = new int[]{5,3,1,3,2,8,6,9,10,4,6,4,8,10,7,4,2,1,6,7};
		CountingSort(arr,arr.length);
		System.out.println(Arrays.toString(arr));
	}
	
	public static void CountingSort(int[] a,int n) {
		if(n<=-1) return;
		
		//查找数组中最大值
		int max = a[0];
		for(int i=1;i<a.length;i++) {
			if(max<a[i]) {
				max = a[i];
			}
		}
		
		//申请一个计数数组C下标为0到max
		int[] c = new int[max+1];
		for(int i=0;i<c.length;i++) {
			c[i] = 0;
		}
		
		//计算每个元素的个数，放入数组C中
		for(int i=0;i<a.length;i++) {
			c[a[i]]++;
		}
		
		//依次累加
		for(int i=0;i<max;i++) {
			c[i+1] = c[i]+c[i+1];
		}
		
		//临时数组R，存储排序之后的数组
		int[] r = new int[a.length];
		//计数排序的关键步骤
		for(int i=a.length-1;i>=0;i--) {
			int index = c[a[i]]-1;
			r[index] = a[i];
			c[a[i]]--;
		}
		
		//将结果拷贝给a数组
		for(int i=0;i<a.length;i++) {
			a[i] = r[i];
		}
	}
}

3.基数排序

先按照数据最后以位来排序，然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过多次排序之后，数据就都有序了。如果数据长度不一致，需要补齐数据到相同长短。

基数排序对要排序的数据是有要求的，需要可以分割出独立的“位”来比较，而且位之间有递进的关系，如果a数据的高位比b数据大，那剩下的低位就不需要较了。除此之外，每一位的数据范围不能太大，才可以用线性排序算法来排序，否则，基数排序的时间复杂度就无法做到O(n)了。

/**
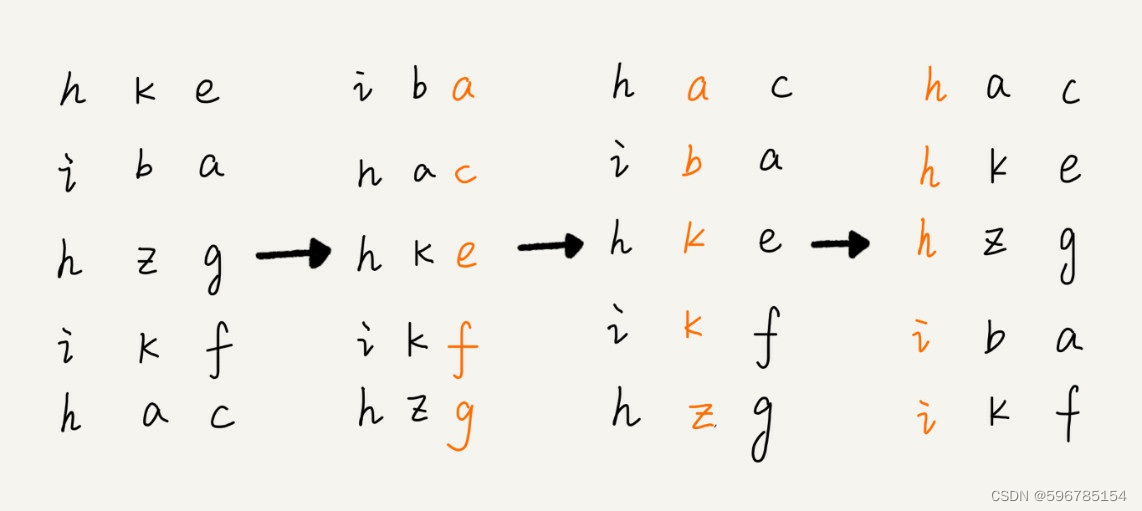
 * 基数排序
 * 原地排序：否
 * 稳定排序：是
 * 空间复杂度：O(d+n) k为数据范围大小
 * 时间复杂度：O(dn) d是维数
 */
public class RadixSort {
	public static void main(String[] args) {
		int[] arrs = new int[] {153,26,78,342,123,241,96};
		
		int max = getMaxData(arrs);
		
		for(int exp=1;max/exp>0;exp=exp*10) {
			CountingSort(arrs,arrs.length,exp);
			System.out.println(Arrays.toString(arrs));
		}
	}
	
	public static int getMaxData(int[] a) {
		//查找数组中最大值
		int max = a[0];
		for(int i=1;i<a.length;i++) {
			if(max<a[i]) {
				max = a[i];
			}
		}
		return max;
	}
	
	public static void CountingSort(int[] a,int n,int exp) {
		if(n<=-1) return;
		
		//查找数组中最大值
		int max = (a[0]/exp)%10;
		for(int i=1;i<a.length;i++) {
			if(max<(a[i]/exp)%10) {
				max = (a[i]/exp)%10;
			}
		}
		
		//申请一个计数数组C下标为0到max
		int[] c = new int[max+1];
		for(int i=0;i<c.length;i++) {
			c[i] = 0;
		}
		
		//计算每个元素的个数，放入数组C中
		for(int i=0;i<a.length;i++) {
			c[(a[i]/exp)%10]++;
		}
		
		//依次累加
		for(int i=0;i<max;i++) {
			c[i+1] = c[i]+c[i+1];
		}
		
		//临时数组R，存储排序之后的数组
		int[] r = new int[a.length];
		//计数排序的关键步骤
		for(int i=a.length-1;i>=0;i--) {
			int index = c[(a[i]/exp)%10]-1;
			r[index] = a[i];
			c[(a[i]/exp)%10]--;
		}
		
		//将结果拷贝给a数组
		for(int i=0;i<a.length;i++) {
			a[i] = r[i];
		}
	}

}