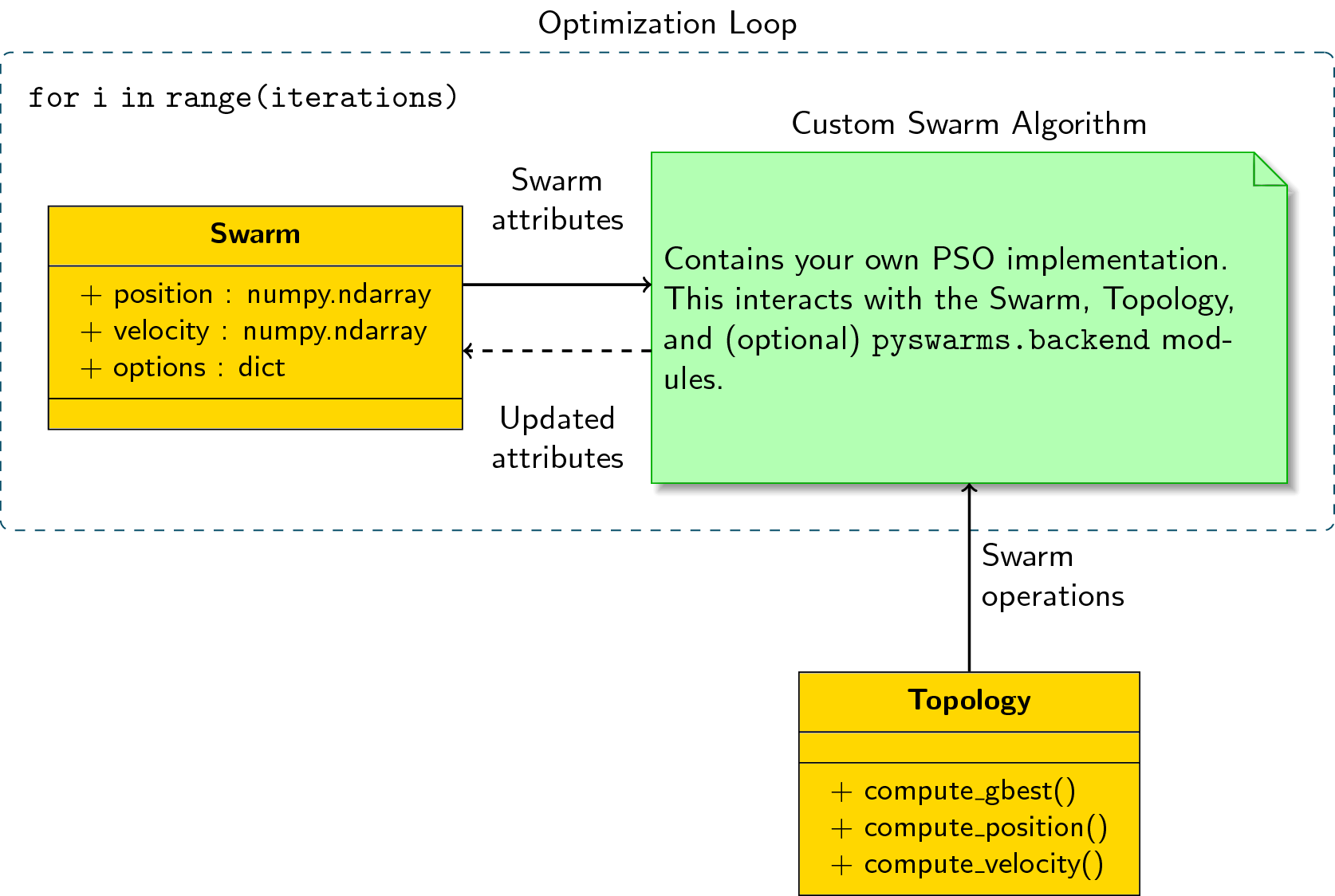
一、知识储备

1.曲线拟合问题的提法

已知一组（二维）数据，即平面上 n个点（xi,yi)  i=1,…,n, 寻求一个函数（曲线）y=f(x), 使 f(x) 在某种准则下与所有数据点最为接近，即曲线拟合得最好．

2.拟合与插值的关系

1）问题：

给定一批数据点，需确定满足特定要求的曲线或曲面

2）解决方案：

若要求所求曲线（面）通过所给所有数据点，就是插值问题；

若不要求曲线（面）通过所有数据点，而是要求它反映对象整体的变化趋势，这就是数据拟合，又称曲线拟合或曲面拟合．

函数插值与曲线拟合都是要根据一组数据构造一个函数作为近似，由于近似的要求不同，二者在数学方法上是完全不同的．

3）实例：

 实例：下面数据是某次实验所得，希望得到X和 f之间的关系？

 

3.曲线拟合的常用方法

3.1 线性最小二乘法

1）线性最小二乘法的基本思路

 2）线性最小二乘法的求解：预备知识

 3）线性最小二乘拟合 f(x)=a1r1(x)+ …+amrm(x)中函数{r1(x),…,rm(x)}的选取  

 二、用MATLAB解拟合问题

1.线性最小二乘拟合 

EG1: 

解法1．用解超定方程的方法

 

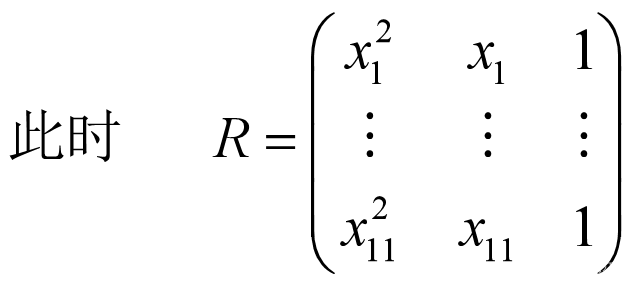
1）输入以下命令：

x=0:0.1:1;
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
R=[(x.^2)' x' ones(11,1)];%生成11行1列的矩阵
A=R\y'

 

 拟合结果：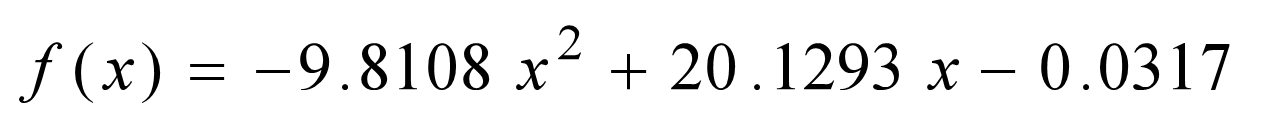

 解法2．用多项式拟合的命令

 x=0:0.1:1;
 y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66   9.56 9.48 9.30 11.2];
 A=polyfit(x,y,2)%输出拟合的多项式系数
 z=polyval(A,x);%拟合下的曲线
 plot(x,y,'k+',x,z,'r') %作出数据点和拟合曲线的图形

2.作非线性最小二乘拟合

 EG2:

 

1）编写M文件 curvefun1.m

function f=curvefun1(x,tdata)
f=x(1)+x(2)*exp(-0.02*x(3)*tdata)   
%其中 x(1)=a;   x(2)=b；x(3)=k;
%关于x和tdata的函数

2）输入命令 

tdata=100:100:1000;
cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];
x0=[0.2,0.05,0.05];%初值
x=lsqcurvefit ('curvefun1',x0,tdata,cdata)
f= curvefun1(x,tdata) 
t=[0:1:1000];
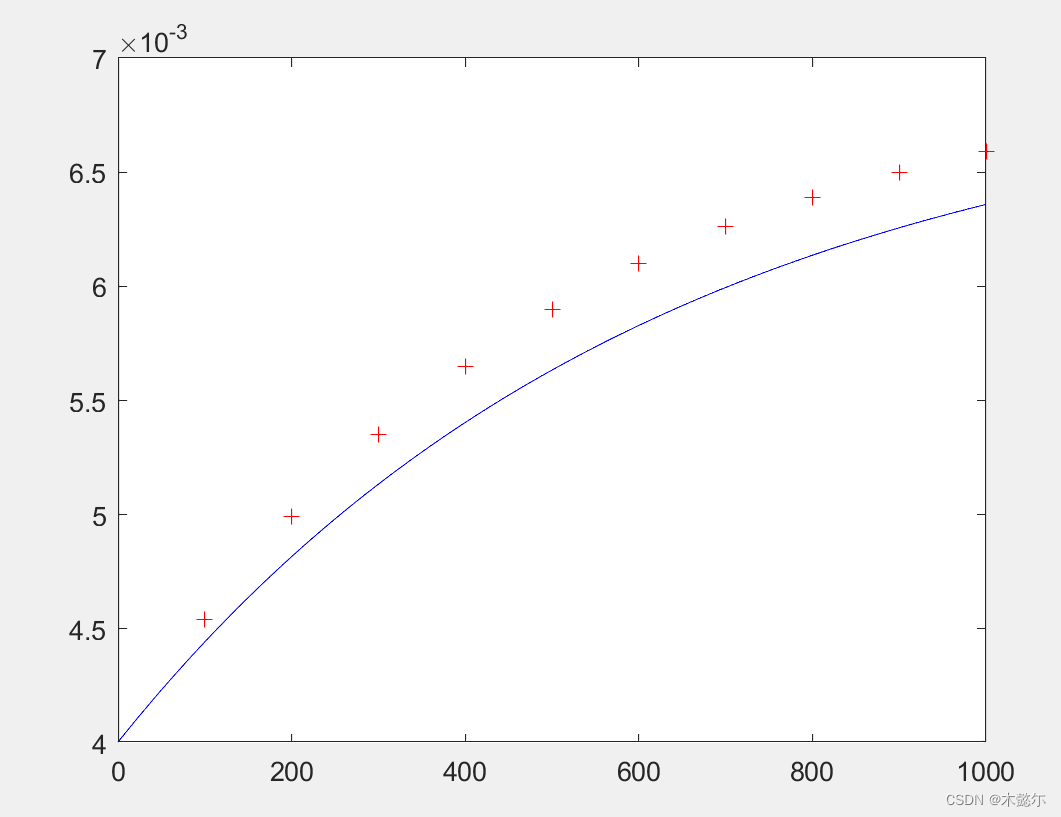
plot(tdata,cdata,'r+',t,curvefun1(x,t),'b')

运行结果：

 结论：a=0.0063, b=-0.0034, k=0.2542 

 

function f=curvefun2(x)
    tdata=100:100:1000;
    cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];
    f=x(1)+x(2)*exp(-0.02*x(3)*tdata)- cdata

x0=[0.2,0.05,0.05];
x=lsqnonlin('curvefun2',x0)
f= curvefun2(x)

 三、练习

1.

clc,clear
x=1:1:10;
y=x.^3-6*x.^2+5*x-3;
xi=rand;%产生0-1的随机数
Y=y+xi;
%一次
f1=polyfit(x,Y,1)%输出多项式次数
y1=polyval(f1,x);%计算各点的拟合值
subplot(2,2,1)
plot(x,y,'x',x,y1)
title("一次拟合曲线")
grid on
%二次
f2=polyfit(x,Y,2)%输出多项式次数
y2=polyval(f2,x);%计算各点的拟合值
subplot(2,2,2)
plot(x,y,'o',x,y2)
title("二次拟合曲线")
grid on
%三次
f3=polyfit(x,Y,3)%输出多项式次数
y3=polyval(f3,x);%计算各点的拟合值
subplot(2,2,3)
plot(x,y,'o',x,y3)
title("三次拟合曲线")
grid on
%四次
f4=polyfit(x,Y,4)%输出多项式次数
y4=polyval(f4,x);%计算各点的拟合值
subplot(2,2,4)
plot(x,y,'o',x,y4)
title("四次拟合曲线")
grid on

 2.

function f=curvefun4(x,tdata)
V=10;
f=V-(V-x(1))*exp(-tdata./x(2))
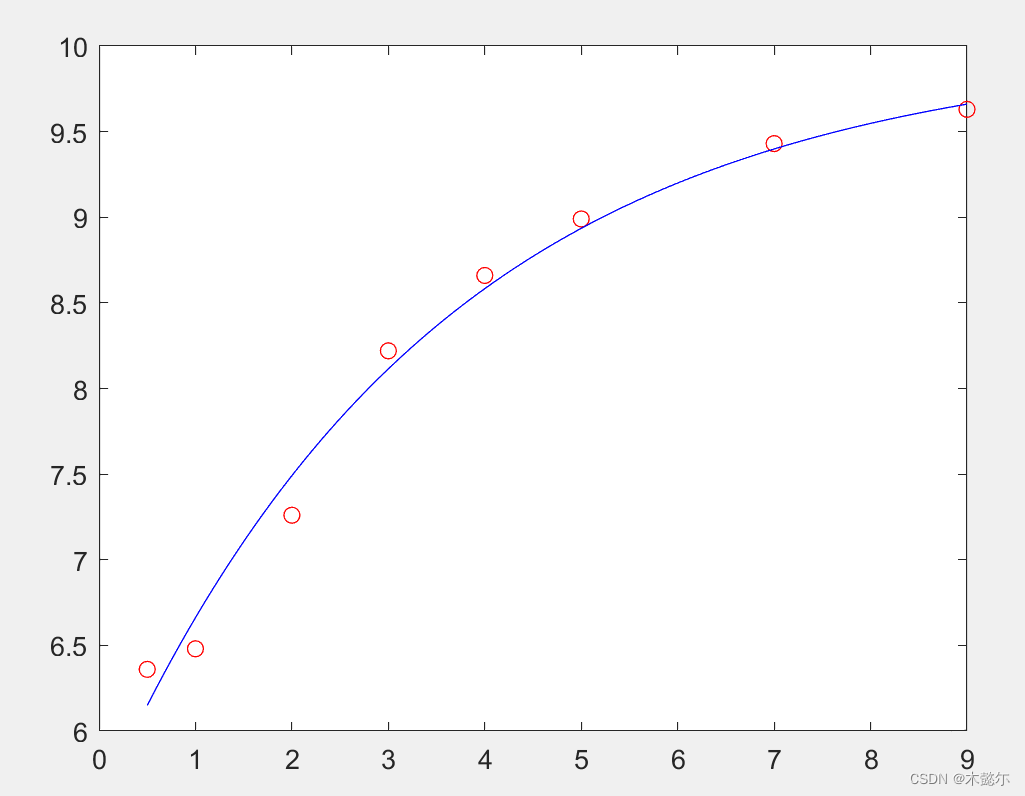
%x(1)=v0;x(2)=T

tdata=[0.5 1 2 3 4 5 7 9];
vdata=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63];
%x0=[0.2,0.05];
x0=[0.1 1];
x=lsqcurvefit('curvefun4',x0,tdata,vdata)
f=curvefun4(x,tdata)
p=linspace(tdata(1),tdata(end));
plot(tdata,vdata,"ro",p,curvefun4(x,p),'b-')