开始系统学习算法啦！为后面力扣和蓝桥杯的刷题做准备！这个专栏将记录自己学习算法是的笔记，包括概念，算法运行过程，以及代码实现，希望能给大家带来帮助，感兴趣的小伙伴欢迎评论区留言或者私信博主哦！今天更新的是《02时间复杂度与空间复杂度》

目录

一、时间复杂度

先决条件

概念

分类

计算规则

案例分析

二、空间复杂度：

概念

示例

---

一、时间复杂度

先决条件

• 一般来说，一个算法执行所消耗的时间从理论上是算不出来的。
• 一个算法花费的时间与算法中语句的执行次数是成正比的。
• 哪个算法语句执行次数多，它花费的时间就多。

概念

1. 对于算法最重要的是数量级和趋势，这些是分析算法主要的部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。
2. 时间复杂度实际上就是一个函数，该函数计算的是执行基本操作的次数。一个算法语句总的执行次数是关于问题规模N的某个函数，记为f(N），N称为问题的规模。语句总的执行次数，记为T[N]，当N不断变化时，T[N]也在不断变化，算法的执行次数的增长速率和f(N)的增长速率相同。则T[N]=O(f(N)),称O(f(N))为时间复杂度的O渐进表示法。

分类

• 算法完成工作最少需要多少基本操作叫做最优时间复杂度，是一种最乐观最理想的状态。
• 算法完成工作最多需要多少基本操作叫做最坏时间复杂度，是算法的一个保障。
• 算法完成工作平均需要多少基本操作叫做平均时间复杂度，它可以均匀全面的评价一个算法的好坏。

计算规则

1. 基本操作,即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法效率时，往往只需要关注操作数量的最高次项，其他次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的时间复杂度都是指最坏时间复杂度

案例分析

见csdn博客：

详解时间复杂度计算公式(附例题细致讲解过程)：

详解时间复杂度计算公式(附例题细致讲解过程)_爱睡觉的咋的博客-CSDN博客_时间复杂度计算公式

没学算法前：三次暴力循环

import time
begin_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a+b+c == 1000 and a**2+b**2 == c**2:
                print("a,b,c:",a,b,c)
end_time = time.time()
print("这段代码一共执行了：",end_time-begin_time,"s")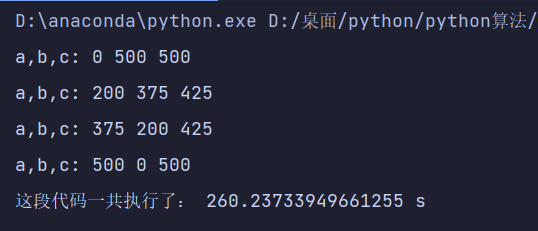

时间复杂度为O(n^3)

学过算法之后：通过abc关系直接生成c：

import time
begin_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        c = 1000-a-b
        if a+b+c == 1000 and a**2+b**2 == c**2:
            print("a,b,c:",a,b,c)
end_time = time.time()
print("这段代码一共执行了：",end_time-begin_time,"s")

时间复杂度为O(n^2)

二、空间复杂度：

概念

一个程序的空间复杂度是指运行完一个程序所需的内存的大小。利用程序的空间复杂度可以对程序的运行所需要的内存多少有一个预先估计。

一个程序执行时，除了需要储存空间和存储本身所使用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两个部分：

• 固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。
• 可变空间。这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。

示例

def reverse(a,b):
    n = len(a)
    for i in range(n):
        b[i] = a[n-1-i]
        #完成列表的逆序

调用reverse方法时，要分配的内存空间包括：引用a，引用b、局部变量n、局部变量i。因此f(n)= 4,该算法的空间复杂度为S（n）=O（1）

注：通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求。当直接要让我们求“复杂度”时，通常指的是时间复杂度。显然对时间复杂度的 追求更是属于算法的潮流！