粒子群优化算法
- 粒子群优化算法简介
- 粒子群优化算法原理
- 粒子群优化算法的数学描述
- 粒子群优化算法框架
- PySwarms:Python中粒子群优化的研究工具包
- PySwarms快速使用
- 示例:编写自己的优化循环
- 相关资料
粒子群优化算法简介
粒子群优化算法(Particle Swarm Optimization[PSO])是在1995年由Eberhart博士和Kennedy博士一起提出的,它源于对鸟群捕食行为的研究。它的基本核心是**利用群体中的个体对信息的共享从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的最优解。**设想这么一个场景:一群鸟进行觅食,而远处有一片玉米地,所有的鸟都不知道玉米地到底在哪里,但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略,也是最简单有效的策略就是搜寻目前距离玉米地最近的鸟群的周围区域。
在PSO中,每个优化问题的解都是搜索空间中的一只鸟,称之为"粒子",而问题的最优解就对应于鸟群中寻找的"玉米地"。所有的粒子都具有一个位置向量(粒子在解空间的位置)和速度向量(决定下次飞行的方向和速度),并可以根据目标函数来计算当前的所在位置的适应值(fitness value),可以将其理解为距离"玉米地"的距离。在每次的迭代中,种群中的粒子除了根据自身的经验(历史位置)进行学习以外,还可以根据种群中最优粒子的"经验"来学习,从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代,最终整个种群的粒子就会逐步趋于最优解。
粒子群优化算法原理
将每个个体表示为粒子。每个个体在某一时刻的位置表示为
x
(
t
)
x(t)
x(t),方向表示为
v
(
t
)
v(t)
v(t):
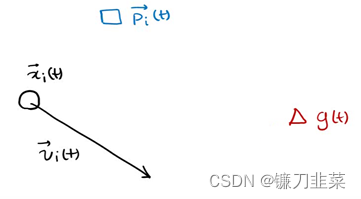
p
(
t
)
p(t)
p(t)为在t时刻x个体的自己的最优解,
g
(
t
)
g(t)
g(t)为在
t
t
t时刻所有个体的最优解,
v
(
t
)
v(t)
v(t)为个体在
t
t
t时刻的方向,
x
(
t
)
x(t)
x(t)为个体在
t
t
t时刻的位置
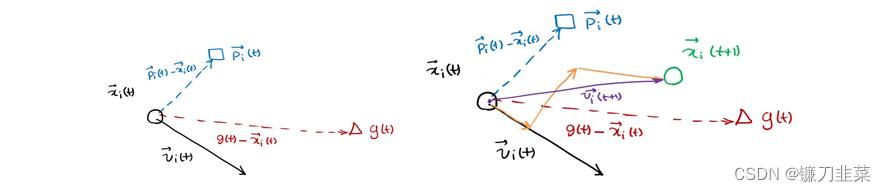
下一个位置为上图所示,由
x
,
p
,
g
x,p,g
x,p,g共同决定了

种群中的粒子通过不断地向自身和种群的历史信息进行学习,从而可以找到问题的最优解。
但是,在后续的研究中表表明,上述原始的公式中存在一个问题:公式中V的更新太具有随机性,从而使整个PSO算法的全局优化能力很强,但是局部搜索能力较差。而实际上,我们需要在算法迭代初期PSO有着较强的全局优化能力,而在算法的后期,整个种群应该具有更强的局部搜索能力。所以根据上述的弊端,shi和Eberhart通过引入惯性权重修改了公式,从而提出了PSO的惯性权重模型:
每一个向量的分量表示如下:
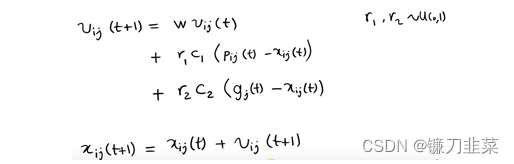
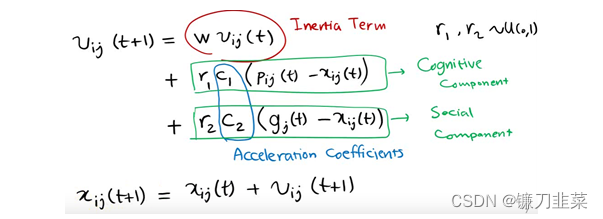
其中w称为PSO的惯性权重,它的取值介于[0,1]之间,一般应用中均采用自适应的取值方法,即一开始令w=0.9, 使得PSO的全局优化能力较强,随着迭代的深入,参数w进行递减,从而使得PSO具有较强的局部优化能力,当迭代结束时,w=0.1。
参数c1和c2成为学习因子,一般设置为1,4961;而r1和r2为介于[0,1]之间的随机概率值。
粒子群优化算法的数学描述
PSO中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子。所有的粒子都有一个由被优化的函数决定的适值(fitness value)(也就是每组组变量所对应的函数值),每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一组随机粒子[随机的一组自变量],然后通过迭代找到最优解。在每一次的迭代中,粒子通过跟踪两个极值来更新自己,第一个就是粒子本身所找到的最优解,称为个体极值;另一个极值是整个种群目前所找到的最优解,这个极值是全局极值。
假设在一个
D
D
D维的目标搜索空间中([也就是
D
D
D元函数]),有
N
N
N个粒子组成一个群落,其中第
i
i
i 个粒子表示为一个
D
D
D维的向量:
X
i
=
(
x
i
1
,
x
i
2
,
.
.
.
,
x
i
D
)
,
i
=
1
,
2
,
.
.
.
,
N
X_i=(x_{i1},x_{i2},...,x_{iD}), i=1,2,...,N
Xi=(xi1,xi2,...,xiD),i=1,2,...,N
第
i
i
i个粒子的飞行速度也是一个
D
D
D维的向量,记为:
V
i
=
(
v
i
1
,
v
i
2
,
.
.
.
,
v
i
D
)
,
i
=
1
,
2
,
.
.
.
,
N
V_i=(v_{i1},v_{i2},...,v_{iD}), i=1,2,...,N
Vi=(vi1,vi2,...,viD),i=1,2,...,N
第
i
i
i个粒子迄今为止搜索到的最优位置称为个体极值,记为:
P
b
e
s
t
=
(
P
i
1
,
P
i
2
,
.
.
.
,
P
i
D
)
,
i
=
1
,
2
,
.
.
.
,
N
P_{best}=(P_{i1},P_{i2},...,P_{iD}),i=1,2,...,N
Pbest=(Pi1,Pi2,...,PiD),i=1,2,...,N
整个粒子群迄今为止搜索到的最优位置为全局极值,记为:
g
b
e
s
t
=
(
P
g
1
,
P
g
2
,
.
.
.
,
P
g
D
)
g_{best}=(P_{g1},P_{g2},...,P_{gD})
gbest=(Pg1,Pg2,...,PgD)
在找到这两个最优值时,粒子需要根据如下公式来更新自己的速度和位置:
v
i
d
=
w
×
v
i
d
+
c
1
r
1
(
P
i
d
−
x
i
d
)
+
c
2
r
2
(
P
g
d
−
x
i
d
)
v_{id}=w\times v_{id}+c_1r_1(P_{id}-x_{id})+c_2r_2(P_{gd}-x_{id})
vid=w×vid+c1r1(Pid−xid)+c2r2(Pgd−xid)
x
i
d
=
x
i
d
+
v
i
d
x_{id}=x_{id}+v_{id}
xid=xid+vid
其中:c1和c2为学习因子,也成为加速常数(acceleration constant), r1和r2为[0,1]范围内的均匀随机数,速度更新公式由三部分组成,第一部分为“惯性”,代表粒子有维持自己先前速度的趋势,第二部分为“认知”部分,反映了对自身历史经验的记忆,代表粒子有向自身历史最佳位置逼近的趋势,第三部分为“社会”部分,反映了粒子之间协同合作与知识共享的群体历史经验。
粒子群优化算法框架
整个粒子群优化算法的算法框架如下:
- step1:种群初始化,可以进行随机初始化或者根据被优化的问题设计特定的初始化方法,然后计算个体的适应值,从而选择出个体的局部最优位置向量和种群的全局最优位置向量。
- step2 迭代设置:设置迭代次数,并令当前迭代次数为1
- step3 速度更新:更新每个个体的速度向量
- step4 位置更新:更新每个个体的位置向量
- step5 局部位置和全局位置向量更新:更新每个个体的局部最优解和种群的全局最优解
- step6 终止条件判断:判断迭代次数时都达到最大迭代次数,如果满足,输出全局最优解,否则继续进行迭代,跳转至step 3。
对于粒子群优化算法的运用,主要是对速度和位置向量迭代算子的设计。迭代算子是否有效将决定整个PSO算法性能的优劣,所以如何设计PSO的迭代算子是PSO算法应用的研究重点和难点。
粒子群算法优化
引入收敛因子,不要惯性权重:
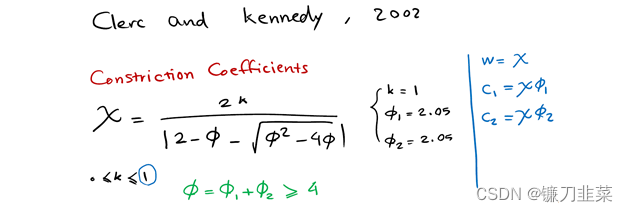
Clerc引入收敛因子(contriction factor)保证收敛性,与使用惯性权重的PSO算法相比,使用收敛因子的PSO有更快的收敛速度。
其实只要恰当的选取,两种算法是一样的。因此使用收敛因子的PSO可以看作使用惯性权重PSO的特例。恰当的选取算法的参数值可以改善算法的性能。
PySwarms:Python中粒子群优化的研究工具包
PySwarms是粒子群优化(PSO)的研究工具包,它提供了一组用于解决连续和组合优化问题的类基元。它遵循黑盒方法,用几行代码解决优化任务,但允许具有一致API的白盒框架用于非标准群模型的快速原型设计。此外,还包括基准目标函数和参数搜索工具,用于评估和改进群体性能。它适用于群体情报研究人员,从业人员和希望在其问题中实施PSO的高级声明性接口的学生。
该软件包的主要设计原则是通过提供丰富的类来解决优化任务来平衡(1)易用性,以及(2)通过定义一致的API来适应非标准PSO,从而实现易于实验实现。在此背景下,PySwarms在其开发过程中遵循以下核心原则:
- 维护一组易于理解的特定约定。这样可以在所有实现中实现可重复性,并创建API所基于的单一框架。因此,对于特定的群S,粒子被定义为m×n矩阵,其中m对应于粒子的数量,并且n对应于搜索空间中的维度的数量。然后将其适应度表示为包含每个粒子的值的m维阵列。
- 为所有swarm实现定义一致的API。一致的API适用于非标准PSO实现的快速原型设计。只要用户根据API实现,所有PySwarms功能都可用。它由初始化swarm的init方法,定义更新行为的update_position和update_velocity规则以及包含进化循环的优化方法组成。
- 为现成的PSO实现提供一组原始类。为了便于访问PSO实现以实现常见的优化任务,我们提供了标准全局最佳和本地最佳PSO的包装类。这些实现遵循相同的PySwarms API,甚至可以构建用于更高级的应用程序。
该工具包的特点为:
- 标准PSO算法的Python实现。包括经典的全局最佳和本地最佳PSO(Kennedy和Eberhart 1995b,1995a),以及用于离散优化的二进制PSO(Kennedy和Eberhart 1997)。这些实现是在numpy中本地构建的(Walt,Colbert和Varoquaux 2011; Jones等人2001-2001–)。
- 内置单目标功能进行测试。提供一组单目标函数来测试优化器。包括简单的变体,如球体功能,以及复杂的变体,如Beale和Rastrigin功能。
- 绘制成本和群体动画的环境。基于matplotlib(Hunter 2007)构建的包装器,可方便地绘制成本和动画群(2D和3D)以评估性能和行为。
- 超参数搜索工具。实现随机搜索和网格搜索,以找到用于控制群体行为的最佳超参数。
- 用于实现自己的优化器的基类。为研究人员提供单目标基类,以快速原型化并实现自己的优化器。
PySwarms快速使用
PySwarms 实现了网格搜索和随机搜索技术,以便为优化器找到最佳参数。
import pyswarms as ps
from pyswarms.utils.search import RandomSearch
from pyswarms.utils.functions import single_obj as fx
if __name__ == '__main__':
# Set-up choices for the parameters
options = {'c1': (1, 5), 'c2': (6, 10), 'w': (2, 5), 'k': (11, 15), 'p': 1}
# 创建一个randomSearch对象
# n_selection_iters是运行搜索器的迭代次数
# iters是运行优化器的迭代次数
g = RandomSearch(ps.single.LocalBestPSO, n_particles=40, dimensions=20, options=options, objective_func=fx.sphere,
iters=10, n_selection_iters=100)
best_score, best_options = g.search()
运行结果:
best_score
Out[3]: 2.3640625294539848
best_options['c1']
Out[4]: 1.3459871461958115
best_options['c2']
Out[5]: 7.054712488266473
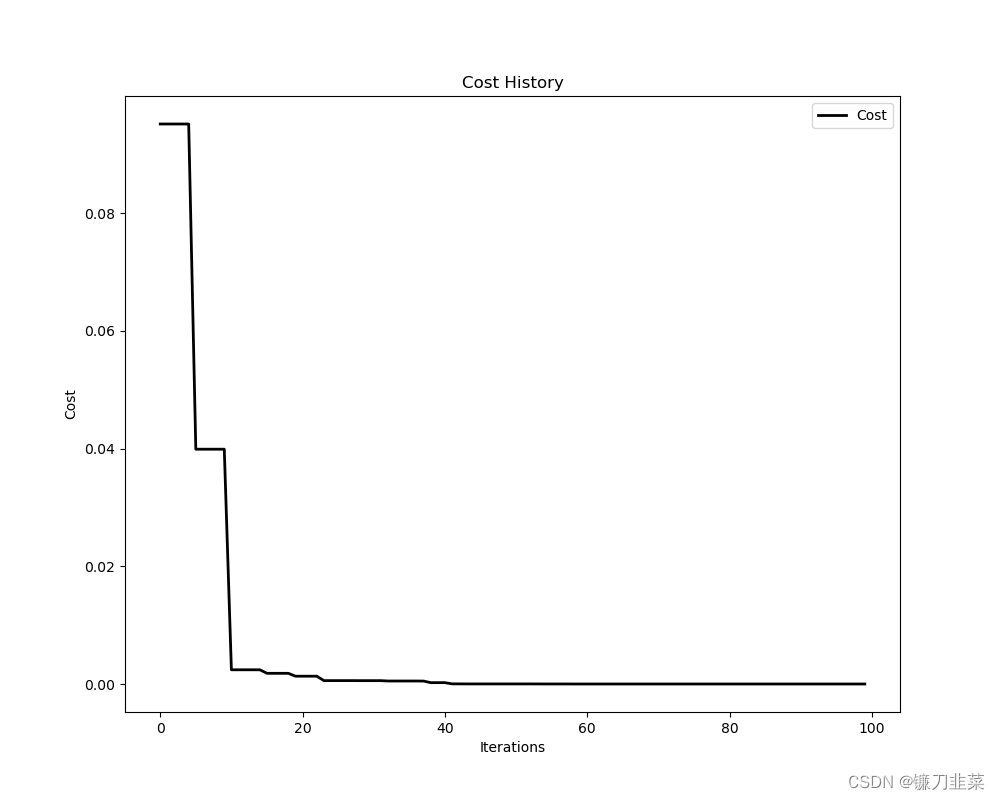
目标函数损失值的可视化:
import pyswarms as ps
from pyswarms.utils.functions import single_obj as fx
from pyswarms.utils.plotters import plot_cost_history, plot_contour, plot_surface
import matplotlib.pyplot as plt
# Set-up optimizer
options = {'c1':0.5, 'c2':0.3, 'w':0.9}
optimizer = ps.single.GlobalBestPSO(n_particles=50, dimensions=2, options=options)
optimizer.optimize(fx.sphere, iters=100)
# Plot the cost
plot_cost_history(optimizer.cost_history)
plt.show()
运行结果:
示例:编写自己的优化循环
本例中,我们将使用pyswarms.backend模块去编写自己的优化循环。我们将尝试使用PySwarms中的native backend重新创建Global best PSO。
首先理解如下示意图:
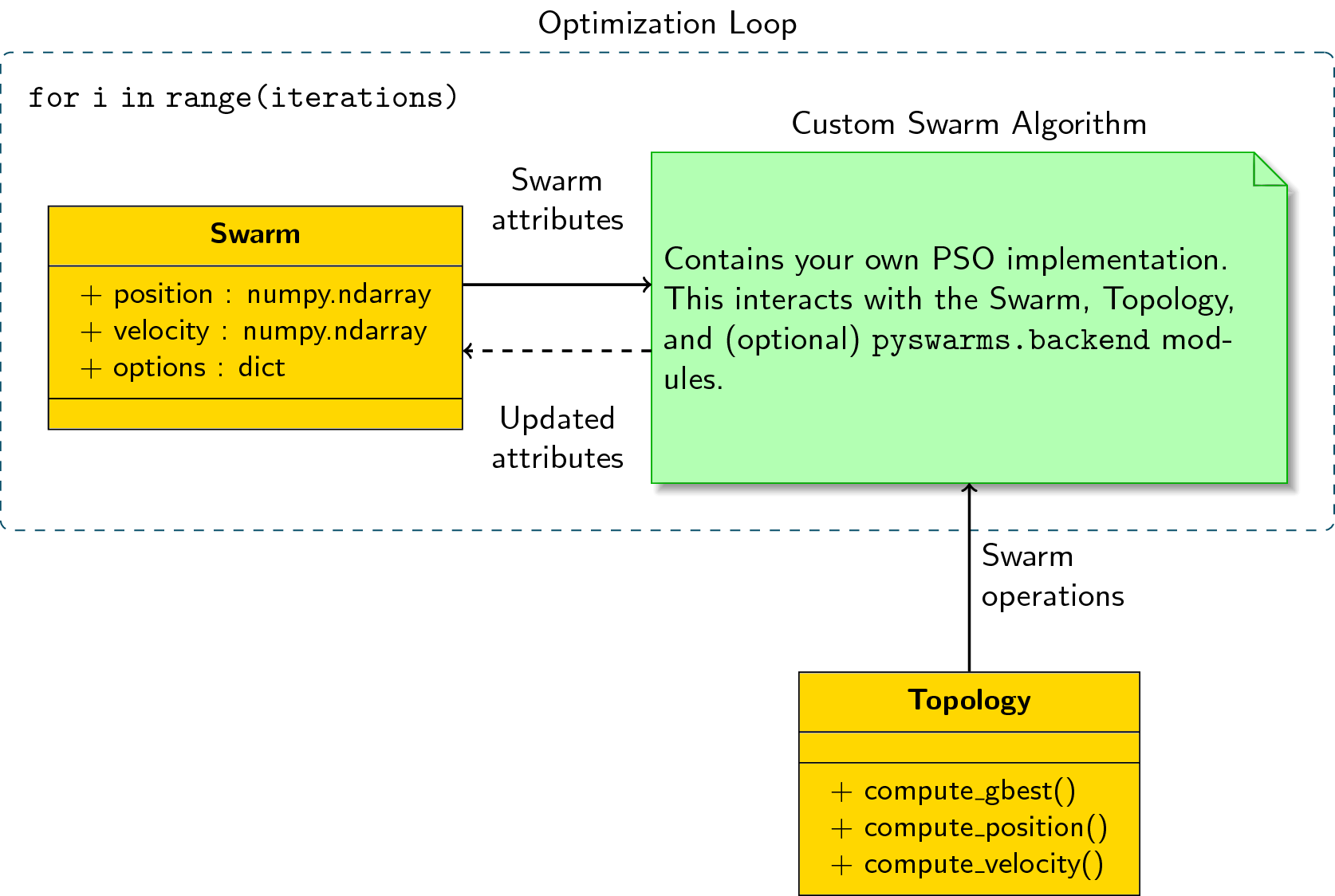
注意:
- 初始化一个
Swarm类,并且在每次迭代中更新它的属性。 - 初始化一个
Topoloy类(在该案例中,我们将使用一个Startopology),并且使用它的方法操作粒子群(Swarm)。 - 还可以使用
pyswarms.backend中的一些附加方法,这取决于我们的需要
因此,对于每次迭代:
- 我们从 Swarm 类获取一个属性。
- 在Topol类的帮助下,根据我们的自定义算法对其进行操作
- 使用新的属性更新 Swarm 类
import numpy as np
# 导入一个sphere函数作为目标函数
from pyswarms.utils.functions.single_obj import sphere as f
# 导入backend模块
import pyswarms.backend as P
from pyswarms.backend.topology import Star
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
原生 global-best PSO实现
现在,全局最佳粒子群优化伪代码如下所示:
for i in range(iterations):
for particle in swarm:
# Part1: If current position is less than the personal best
if f(current_position[particle]) < f(personal_best[particle]):
# 更新personal best
personal_best[particle] = current_position[particle]
# Part2: If personal best is less than global best,
if f(personal_best[particle]) < f(global_best):
# 更新global best
global_best = personal_best[particle]
# Part3: 更新velocity和position matrices
update_velocity()
update_position()
如上所示,标准PSO是一个三部分组成的策略:①更新个体粒子最优值;②更新全局最优值;③更新速度和位置矩阵。
下面,我们将按照这样的三步走策略使用PySwarms backend实现我们自己的代码:
让我们做一个有50个粒子的二维群(2-dimensional swarm)来优化sphere function。首先,初始化算法中的重要属性:
my_topology = Star() # The Topology Class
my_options = {'c1': 0.6, 'c2': 0.3, 'w': 0.4} # 任意设置
my_swarm = P.create_swarm(n_particles=50, dimensions=2, options=my_options) # The Swarm class
print('下列是我们自定义的swarm的属性:{}'.format(my_swarm.__dict__.keys()))
输出:
下列是我们自定义的swarm的属性:dict_keys(['position', 'velocity', 'n_particles', 'dimensions', 'options', 'pbest_pos', 'best_pos', 'pbest_cost', 'best_cost', 'current_cost'])
现在,编写我们的优化循环:
iterations = 100
for i in range(iterations):
# Part1: 更新personal best
my_swarm.current_cost = f(my_swarm.position) # 计算current cost
my_swarm.pbest_cost = f(my_swarm.pbest_pos) # 计算personal best pos
my_swarm.pbest_pos, my_swarm.pbest_cost = P.compute_pbest(my_swarm) # 更新和存储
# Part2: 更新global best
# 注意:gbest计算取决于自己的topology
if np.min(my_swarm.pbest_cost) < my_swarm.best_cost:
my_swarm.best_pos, my_swarm.best_cost = my_topology.compute_gbest(my_swarm)
# 打印输出
if i % 20 == 0:
print('Iteration: {} | my_swarm.best_cost:{:.4f}'.format(i + 1, my_swarm.best_cost))
# Part3: 更新位置和速度矩阵
# 注意:位置和速度更新取决于自己的topology
my_swarm.velocity = my_topology.compute_velocity(my_swarm)
my_swarm.position = my_topology.compute_position(my_swarm)
print("The best cost found by our swarm is {:.4f}".format(my_swarm.best_cost))
print("The best position found by out swarm is {}".format(my_swarm.best_pos))
输出:
Iteration: 1 | my_swarm.best_cost:0.0000
Iteration: 21 | my_swarm.best_cost:0.0000
Iteration: 41 | my_swarm.best_cost:0.0000
Iteration: 61 | my_swarm.best_cost:0.0000
Iteration: 81 | my_swarm.best_cost:0.0000
The best cost found by our swarm is 0.0000
The best position found by out swarm is [2.99544966e-69 8.25780144e-70]
当然,我们也可以仅仅在在 PySwarms 中使用 GlobalBestPSO 实现(它有boundary support, tolerance, initial positions,等):
from pyswarms.single import GlobalBestPSO
optimizer = GlobalBestPSO(n_particles=50, dimensions=2, options=my_options)
optimizer.optimize(f, iters=100)
输出:
(0.0007926519919657612, array([0.02352951, 0.01546008]))
一个完整的代码:
import pyswarms as ps
from pyswarms.utils.functions import single_obj as fx
# 根据参数初始化粒子群
# 参数由一个字典输入, c1 c2 分别是个体/群体加速常数, w 是惯性权重
# 此外还有两个可选参数 k (考虑邻居的数量) 和 p (要使用的闵可夫斯基 p-范数)
options = {'c1': 0.5, 'c2': 0.3, 'w':0.9}
dimensions = 2 # 设置粒子的维度, 也就是有几个 feature
# 此外可以设定粒子所在的位置, 例如,我们规定所有粒子的所有维度的值都应当位于 (-5, 5) 之间
max_bound = 5 * np.ones(dimensions)
min_bound = - max_bound
bounds = (min_bound, max_bound)
# n_particles: 粒子群中的粒子数量, dimensions: 每个粒子的维度 options: 参数选项, bounds: 粒子范围限制
optimizer = ps.single.GlobalBestPSO(n_particles=10, dimensions=dimensions, options=options, bounds=bounds)
# 求解
obj_fun = fx.rastrigin # 目标函数
# obj_fun: 要优化的目标函数 iters: 迭代次数, verbose: 输出信息的冗长形式
# 第一个返回值是最小cost, 第二个返回值是最小cost 对应的粒子位置(pos)
cost, pos = optimizer.optimize(obj_fun, iters=1000, verbose=3)
输出:
2022-12-12 21:40:48,431 - pyswarms.single.global_best - INFO - Optimize for 1000 iters with {'c1': 0.5, 'c2': 0.3, 'w': 0.9}
pyswarms.single.global_best: 100%|██████████|1000/1000, best_cost=0
2022-12-12 21:40:49,021 - pyswarms.single.global_best - INFO - Optimization finished | best cost: 0.0, best pos: [-4.26451421e-10 1.79975206e-09]
相关资料
[1] PySwarms’s documentation
[2] https://zhuanlan.zhihu.com/p/80766325
[3] 粒子群算法的 python 实现与可视化
[4] 使用 PySwarms 实现自定义目标函数的粒子群优化
[5] python 粒子群算法
[6] PySwarms(Python粒子群优化工具包)的使用:GlobalBestPSO例子解析
[7] 粒子群算法(PSO)的数学原理
[8] 粒子群算法