CF原题链接

题目大意:n个结点,每个结点有一个正数值。现在让你在n个点间进行边的连接,唯一限制条件是不能出现这种情况:如3个点A,B,C,且A<=B<=C,那么不能同时出现边(A,B)和边(B,C)。请问,最多可以连接多少条边。
分析:虽然题目用到图结构的点和边的概念,但是显然此题目和图结构的几大算法(最小树,最短路径,拓扑)没有什么关联。
此类题目首要任务是读懂题目,然后需要根据样例数据分析解法,好在CF题目通常都会给多组数据。先放一张草稿纸,做算法和数学题其实区别不大(都得用草稿纸作为我们的拓展内存使用)。不要关注草稿纸内容..........................和题解无关

在草稿纸上罗列下数据。介绍下个人的分析过程,分析过程和结论如下:
首先我们应该将数据排序,值相同的记录在一起例如样例2的6个数字5 2 3 1 5 2
我们应该排序得到1 2 2 3 5 5
(1)如果两个点值相同,那么将这两点连边是特别不经济的,就是说如果A==B,如果边(A,B),那么A和B两个点都不能和其他任何点(无论大小)进行连边。只有一种情况才会连接值相同的点,那就是整个序列如样例4哪样,所有结点值相同,没有其他节点。
(2)如果有A<B,那么如果将A和B连边,那么所有比A小的都不能和A连,同样,所有比B大的不能和B连。但是比A小的和B连接没有问题,同样,比B大和A连接也不成问题。
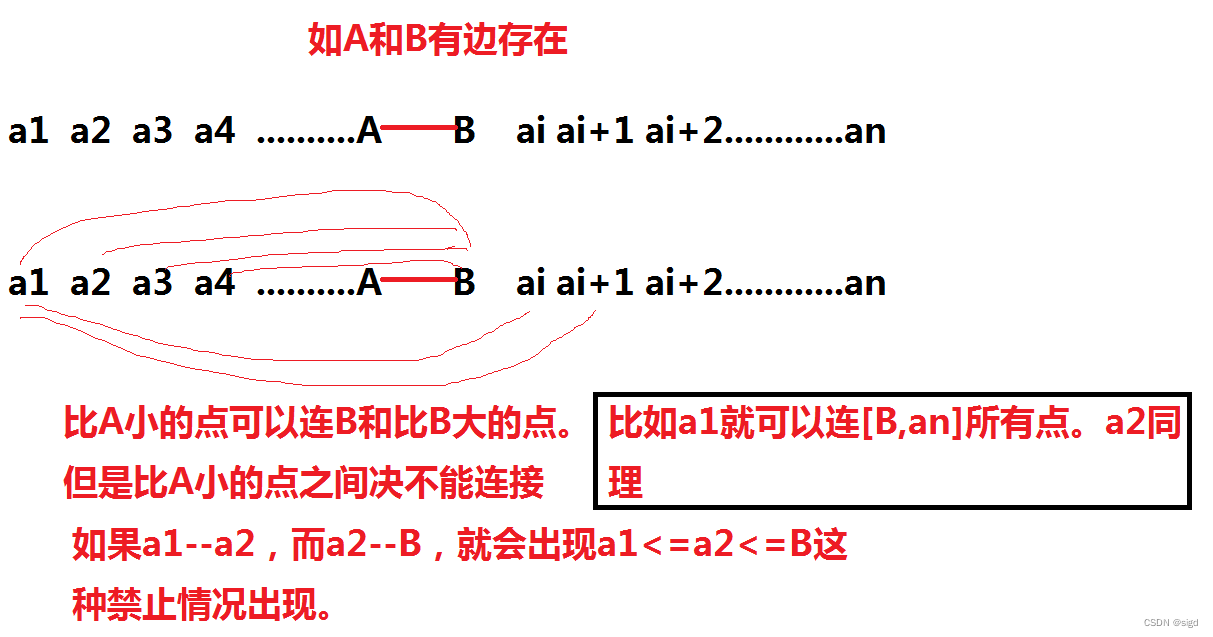
这时发现实际A也是可以连接到[B,an]区间的所有点。
(3)那么A和B应该怎么选取呢?直觉上A和B应该是值相邻的结点,如果A和B之间还有其他结点,例如C,A<C<B,那么不选择C显然不对,因此C同样可以和a1,a2.....连接,同样可以和B连接(那么C不就是我们想要的那个A吗),所有在枚举A和B的时候,A,B必为相邻结点。
(4)其实第一次做答的时候我就直接按照上面分析1,2,3写代码提交通过了。后续进一步思考发现,枚举A和B实际上就是枚举A,简言之[a1,A]的所有结点都和[B,an]所有结点连边,而B就是A的下一个元素。因此,枚举结点A即可,A左侧所有结点和A右侧所有结点可以连边。
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main()
{
ios::sync_with_stdio(0),cin.tie(0);
long long i,j,t,n,a[200005];
cin>>t;
while(t--)
{
cin>>n;
for(i=1;i<=n;i++)
cin>>a[i];
sort(a+1,a+n+1);
a[n+1]=-1;/**< 特殊值,方便处理第n个元素 */
long long ans=0,len=1;/**< 不开longlong会错哦 */
for(i=2;i<=n+1;i++)
if(a[i]!=a[i-1])/**< 枚举结点A,A和它下一个元素值不同,注意A是a[i-1] */
ans=max(ans,(i-1)*(n-i+1));/**< 左边i-1个和右边n-i+1个元素都可以连边 */
if(ans==0)/**< 处理所有值都相同的特殊情况 */
ans=n/2;
cout<<ans<<endl;
}
return 0;
}
有兴趣可以做下此次比赛1,2题,第1题是很有CF特色的题目。