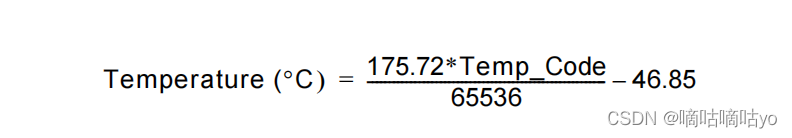目录
一、舒尔特方格简介
二、如何生成舒尔特方格
(一)线性同余法
1、利用线性同余法生成随机数序列的规律
(1) 当a和c选取合适的数时,可以生成周期为m的随机数序列
(2) 种子seed取值也是有周期的
2、利用线性同余法生成5阶舒尔特方格的程序
(1)先验证当x0不变时,生成的随机数序列是有周期的
(2)验证seed值x0也具有周期性
(3)生成5维舒尔特方格数字
(二)利用rand()函数
1、rand()函数搭配srand(time(NULL))函数
2、动态取模法
(1)初始化
(2)随机将a中数据存入b中
3、图解动态取模法
(1)a、b初始状态
(2)生成第一个随机数
(3)生成第二个随机数
(4)执行最后一步
4、动态取模法代码
rand()随机函数可以用来生成舒尔特方格数字。下边先介绍一下舒尔特方格。
一、舒尔特方格简介
舒尔特方格是用来测试和训练专注力的,百度百科的介绍如下:
舒尔特方格,画一张有25个小方格(规格1cm*1cm)的表格,将1~25的数字顺序打乱,填在表格里面,然后以最快速度从1数到25,要边读边指出,一人指读一人帮忙计时。
采用盯点法就可以随时训练的,在教室和家里,每天盯着某个点和物体看上几分钟就可以的,还可以采用舒尔特训练法。
运用这种方法的时候,可以自制几套卡片,绘制表格,任意填上数字。从 1开始,边念边指出相应的数字,直到25为止。同时诵读出声,施测者一旁记录所用时间。数完 25 个数字所用时间越短,注意力水平越高。以 12 —— 14 岁年龄组为例,能达到 16 "以上为优秀, 26 "属于中等水平, 36 "则需要进行强化提高。

注:百度百科上介绍的舒尔特方格是5维(5行5列)规格的,而实际维数是可变的,维数越高难度越大,1维2维太简单,一般不用。3维、4维属于初级难度,5维6维属于中级难度,7级及以上就属于难度比较高级的了。
二、如何生成舒尔特方格
5维舒尔特方格内数字的排列不是固定的,位置是随机的,运用排列组合的知识可以知道,一共有25!个不同的排列方式。用人工排列生成的方法显然是不可行的,那么用什么算法可以实现这个目的呢?下边介绍两种方法。
(一)线性同余法
在上一篇文章中介绍了线性同余生成随机数的方法。线性同余的公式如下所示:
(1)
其中a是乘法器,c是增值,m是模,这三个都是常数,是生成的随机数序列,当n=0时,
的值称为种子seed。
1、利用线性同余法生成随机数序列的规律
(1) 当a和c选取合适的数时,可以生成周期为m的随机数序列
周期为m的意思就是,在一个周期内,利用公式(1)迭代计算m次,正好可以把数字0~m-1每个数字都可以生成且只生成一次,而且最后一次迭代生成的数正好就是种子数。迭代到第m+1次时,生成的数字和第一次迭代生成的数字
一样,再接着迭代就会重复上一个周期。生成一个周期内的数字排列顺序表面看是无规律,实际上是由公式(1)计算出来的,所以叫伪随机数。
还需要注意,并不是任意取一组a和c,就可以生成周期为m的伪随机数序列。a和c的取值是有限定条件的,条件如下图所示。

(2) 种子seed取值也是有周期的
利用公式(1),当a、c、m都确定后,当seed值选取不同时,生成的随机数序列也不同。但是需要注意,并不是任意取一个seed值,生成的随机数序列都不一样,seed取值也是有周期的,当随机数的周期是m时,seed的周期也是m。也就是seed=0时,和seed=m时,生成的随机数序列是一样的。也就是利用线性同余方法,生成不同的随机数序列最多有m种。
2、利用线性同余法生成5阶舒尔特方格的程序
5阶舒尔特方格的数字范围为1~25,每个格子数字各不相同,排列顺序随机。所以可以考虑使用线性同余法。经过测试,发现当c=11,a=11时,利用线性同余计算出来的伪随机数序列的周期是25。
(1)先验证当x0不变时,生成的随机数序列是有周期的
编写一个给定x0=0,生成两个周期随机数的测试程序如下:
#include <iostream>
using namespace std;
int main()
{
int i,x0=0,a=11,c=11,m=25; //确定a=11,c=11,m=25
for(i=0;i<m*2;i++) //此循环用于生成2个周期内的随机数
{
x0=(a*x0+c)%m;
cout<<x0<<" ";
}
cout<<endl;
return 0;
} 下图是测试结果,图中黄色框内是第一个周期的25个随机数,绿色框内是第二个周期内的25个随机数。可以看出两个周期内的随机数排列顺序完全一致,因此说明当x0不变时,生成的随机数呈周期性变化。

(2)验证seed值x0也具有周期性
编写一个x0从0增加到49(两个周期)时,每个seed值生成一个周期的随机函数序列,代码如下:
#include <iostream>
using namespace std;
int main()
{
int i,j,x0,a=11,c=11,m=25; //确定a=11,c=11,m=25
for(j=0;j<m*2;j++) //此循环用于使种子值从0增加到49
{
x0=j;
cout<<"seed="<<x0<<":";
for(i=0;i<m;i++) //此循环用于生成一个周期内
{
x0=(a*x0+c)%m;
cout<<x0<<" ";
}
cout<<endl;
}
return 0;
} 下图是测试结果如下图,从图中可以发现,seed值在0~24范围内(黄线以上),生成的25个随机数序列各不相同,而seed在25~49范围内(黄线以下)时的随机序列,与0~24范围内依次对应,完全一样,说明,seed值对随机序列的影响也是周期性的,周期也是25。

综上所述,利用基本的线性同余算法,对于5维舒尔特方格,最多只能生成25个不同的排列。
(3)生成5维舒尔特方格数字
本例程序,将生成的25个5维舒尔特方格数字输出到一个csv文件内。因为利用线性同余算法生成的随机数范围为0~24,而5维舒尔特方格内的数字为1~25,所以只需将生成的随机数再加1即可。
#include <iostream>
#include <fstream>
using namespace std;
int main()
{
int i,j,x0,a=11,c=11,m=25; //确定a=11,c=11,m=25
ofstream oFile; //新建一个ofstream文件oFile
oFile.open("ShultGrid.csv",ios::out|ios::trunc);//打开oFile文件,文件名称为"ShultGrid.csv"
for(j=0;j<m;j++) //此循环用于使种子值从0增加到49
{
x0=j;
oFile<<"舒尔特方格"<<x0;
for(i=0;i<m;i++) //此循环用于生成一个周期内
{
x0=(a*x0+c)%m;
if(i%5==0) //每5个数字分成一行
{
oFile<<endl;
}
oFile<<x0+1<<","; //生成的随机数为0~24,加1后变为1~25。输入一个",",代表光标移动到同一行的下一个单元格
}
oFile<<endl<<endl; //最后一行回车,然后再空一行
}
return 0;
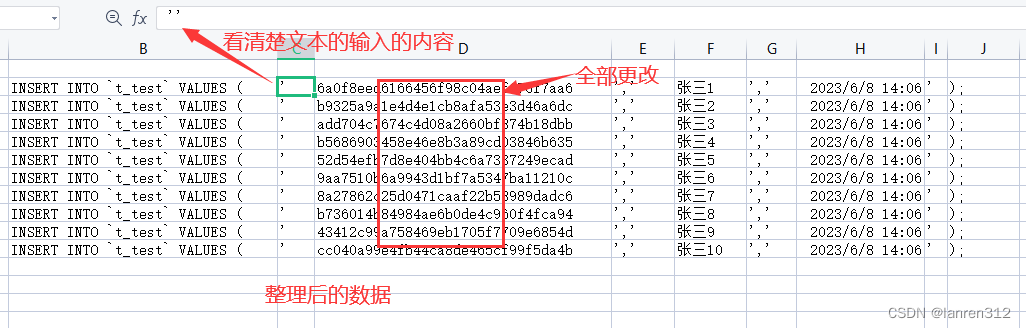
} 以下是程序运行后,生成的csv文件部分舒尔特方格截图。

(二)利用rand()函数
以上介绍了利用线性同余法生成舒尔特方格的方法,方法比较简单,但是最大的缺点是只能生成25个不同的排列。要想生成更多不同的排列,还需要用其他的方法。而利用rand()函数就是一种可行的方法。
1、rand()函数搭配srand(time(NULL))函数
在上一讲种介绍了,可以利用rand()搭配srand(time(NULL))函数,生成1~25的随机数,代码如下所示。
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <windows.h>
#include <stdio.h>
#include <unistd.h>
#include <sys/types.h>
using namespace std;
int main()
{
int m,n;
cin>>n>>m;
// srand(getpid());
srand(time(NULL));
while(1)
{
cout<<rand()%(m-n+1)+n<<endl;
Sleep(1000);
}
}运行代码,输入n=1,m=25,生成的结果如下图所示。从图中可以看出,在前25个数中,有重复的数字,还缺了一些数字。这是因为rand()函数是以32768为模,在一个周期内可以生成0~32767范围内互不相同的随机数序列。但是rand()%25的结果就可能在0~25范围内会出现重复或者缺失的情况。

所以,用这种方法是不可行的。
2、动态取模法
本例提出了一种新的方法实现不同维数舒尔特方格的生成方法,也需要用到rand()、srand()函数,在算法上采用动态取模方法。
动态取模算法的思路是:
(1)初始化
声明两个长度为25的一维数组a[25],b[25],数组a用来按顺序存放1~25数字,b用来存放从a中随机取出来的数字。用j表示数组b的角标,i表示数组a[]的角标,k表示需要更新数据的a[]的角标。
(2)随机将a中数据存入b中
从j=0开始,依次随机将a中的一个数字,存入到b[j]中,然后将a中角标i以后的有效数字依次向前移动一位。此时a[i]就被覆盖了,而a[24-j]那个位置的数据就无效了,下次取数字就不会再考虑这个位置。a中有效数字就是a中还没有被存入到b中的数字。a的角标i是用srand()搭配rand()%(25-j)随机生成的。此步关键代码为
srand(time(NULL));
i=rand()%(25-j);
b[j]=a[i];
a[i]=a[i+1];模m=25-j,是可变的,因为每次从a中取走一个数字,a中的有效数字就减少了一个,所以生成的随机数范围就要减少1,也就是模m是依次减少1,是动态可变的,所以叫动态取模法。
3、图解动态取模法
(1)a、b初始状态
a、b初始化后的状态如下图所示。

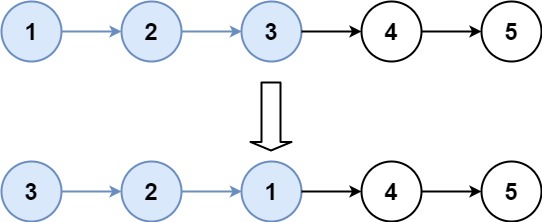
(2)生成第一个随机数
假设第一次i=3,则把a[3]的值4赋给b[0],然后从i=3开始,到i=23结束,执行a[i]=a[i+1]进行数据更新。a、b数组执行生成随机数前后的对比如下图所示。图中a数组中有效的数字所占据的空间用绿色填充,无效的空间用白色填充。数组b中已经填入的随机数字用蓝色填充,没有填入数字的用白色填充。

(3)生成第二个随机数
假设第二次i=22,那么取出其中存储的数据24,放入b[1]中,然后从i=22开始,到i=22结束,执行a[i]=a[i+1]进行数据更新。a、b数组执行生成随机数前后的对比如下图所示。

(4)执行最后一步
执行到第25步时,a、b数组内的存储情况如下图所示。

4、动态取模法代码
#include <iostream>
#include<stdio.h>
#include <cstdlib>
#include <ctime>
#include <fstream>
#include <string>
using namespace std;
int* diff_random(int m,int num)
{
int a[num];//a数组用于按1-num顺序存放初始数字,b用于存放随机生成的舒尔特数字
int *b=new int[num];
int i,j,k;
for(i=0;i<num;i++)//初始化初始数字数组
{
a[i]=i+m;
}
srand(time(NULL));
for(j=0;j<num;j++) //利用无重复随机数算法生成舒尔特方格数组,j为生成数组的序号
{
i=rand()%(num-j); //生成数组a的随机序号,范围为0~num-j,用i表示
b[j]=a[i]; //将a[i]中存放的数字(也就是i+1)赋值给b[j]
for(k=i;k<num-j-1;k++) //将a[i]中存放的数字删除,将a[i+1]~a[num-j]的数字依次向前移动一个位置
{
a[k]=a[k+1];
}
}
for(i=0;i<num;i++) //初始化初始数字数组
{
cout<<a[i]<<endl;
}
return b;
}
int main()
{
int dim,num;//dim:舒尔特方格维数,num:方格个数
cout<<"请输入舒尔特方格维数:"<<endl;
cin>>dim;
num=dim*dim;
int i;
int *b=diff_random(1,num);
ofstream oFile;//新建一个ofstream文件oFile
oFile.open("ShultGrid1.csv",ios::out|ios::trunc);//打开oFile文件,文件名称为"ShultGrid.csv"
oFile<<dim<<"维舒尔特方格"<<endl;
for(i=0;i<num;i++)
{
oFile<<b[i]<<",";
if((i+1)%dim==0)
{
oFile<<endl;
}
}
oFile.close();
cout<<dim<<"维舒尔特方格已生成,请打开ShultGrid1.csv文件查阅"<<endl;
return 0;
}