目录

一、概述

二、数学模型 

2.1 机会约束决策的情景方法

2.2 带有测量的情景方法

三、 机会约束决策的一种快速方法

3.1 通过仿射变换进行近似调节

3.2 可行域的仿射变换

3.3 两阶段决策算法

四、算例——配电网

4.1 防止过电压的有功功率削减

4.2 数值模拟

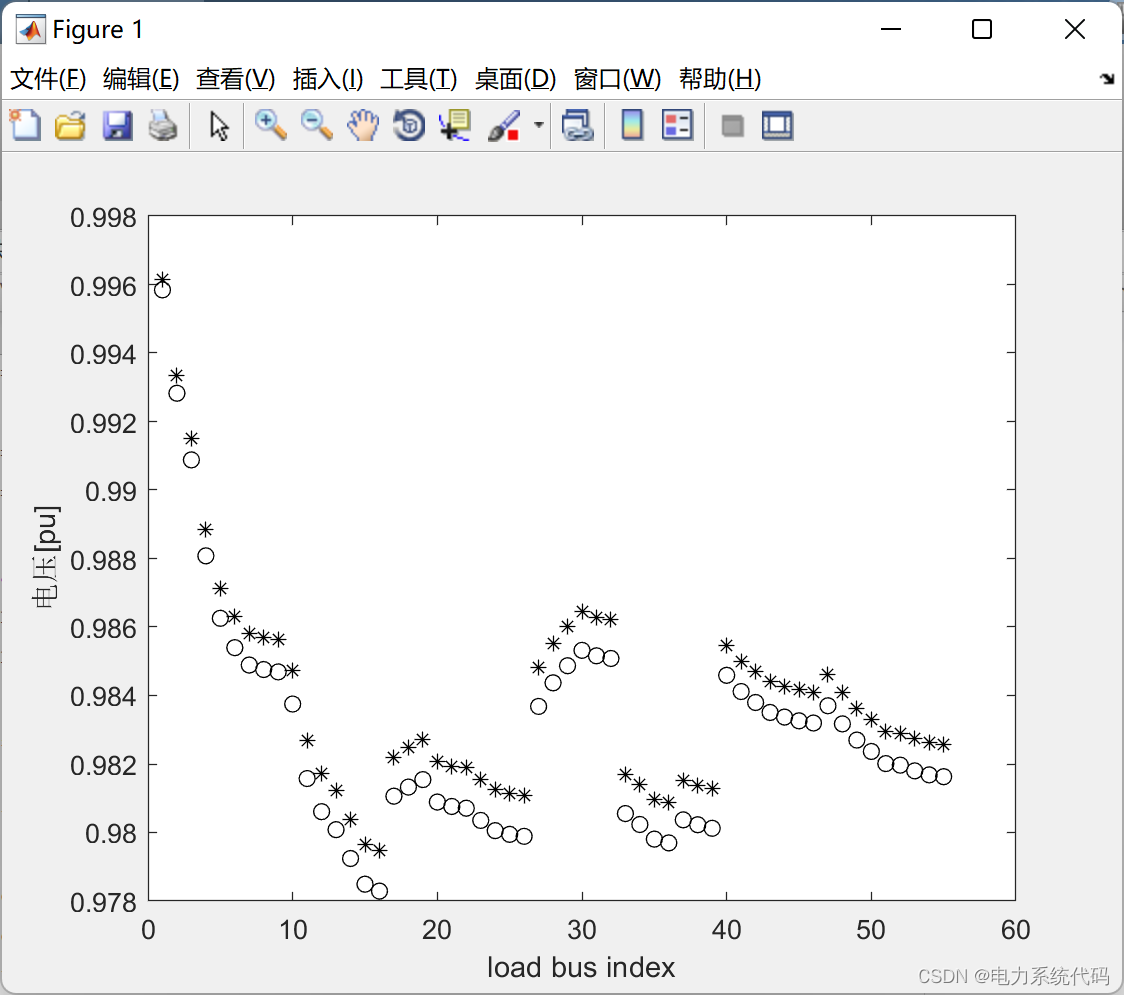
 4.3 运行结果

5 Matlab代码实现

---

一、概述

许多工程问题可以表述为不确定下的决策实例，即当问题参数不确定时，做出满足某些给定约束的具有成本效益的决策的问题。一种自然的方法是做出一个保证对于未知参数的任何可能的可接受值都是可行的决定，因此采用最坏情况范式。在某些应用中，这种稳健的方法产生易于处理的程序，可以找到最佳解决方案。这样的解决方案在可实现的性能方面可能非常保守：决策可能会受到参数的极值的影响，这些极值极不可能但对寻求最优决策的可行区域有严重影响。

第二种方法在于制定所谓的机会约束决策问题。在这些问题中，可以容忍对于在参数空间中具有最小概率度量的一组参数值可以违反问题的约束，因此不太可能实现。这种方法允许在安全性（旨在违反约束的概率）与性能（决策成本）之间进行权衡。机会约束问题通常是非凸的并且难以解决，即使具有已知参数值的原始问题是凸的。然而，它们可以通过采用所谓的场景方法来有效地解决，其中随机约束被确定性约束所取代，通过对参数不确定性进行采样获得。如果约束的数量足够大，则可以以高置信度保证机会约束意义上的可行性。相反，也可以保证通过这种方法获得的解决方案的成本。

在本文中，我们考虑了具有特定结构的机会约束决策问题：一方面，我们假设有关决策问题未知参数的一些先验信息是已知的，以样本的形式存在；另一方面，我们假设可以通过测量收集有关这些参数真实值的进一步信息。我们对场景方法进行了专门化，以便可以有效地使用先验样本以及可用的度量，以生成满足机会约束的可行区域。这导致了一个两阶段算法，由样本的离线预处理组成，然后是在线部分，需要在测量可用时立即执行。该在线部分在计算时间和内存占用方面都非常轻量级，因此适合在嵌入式系统中实现。作为选择的一个应用，我们考虑配电网中微型发电机的控制。

在第二节中，我们简要回顾了情景方法，并用测量制定了机会受限的决策问题。在第三节，展示了如何近似未知参数的后验分布，并且分析了一种解决机会约束决策问题的快速算法。在第四节中，说明所提出的配电网实时运行算法的有效性。

二、数学模型 

2.1 机会约束决策的情景方法

考虑机会约束决策问题：

       

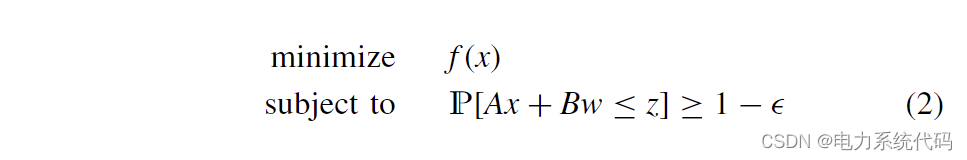
其中 x ∈ Rn 是决策变量，f (x) 是凸成本， 是建模为随机变量的未知干扰， 是常数项。我们假设随机变量 w 的支持被赋予了一个 σ -代数 D 并且 P在 D 上定义。最后， ∈ (0, 1) 是期望的违反约束的概率。

一般的机会约束决策问题是非凸的，并且通常在计算上难以处理。请注意，我们假设线性约束在随机变量中是仿射的。在这种情况下，只要 w 的基本分布已知，就可以获得分析结果，为机会约束问题重新表述为凸问题提供条件。在任何其他情况下，情景方法都是将随机程序转换为这种形式的确定性问题：

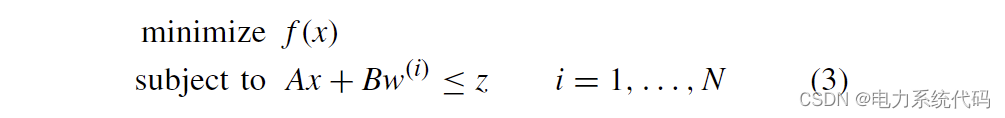
其中是随机扰动的 N 个样本。如果 N 足够大，那么这个数学描述等价于上面一个数学描述。

场景方法明显没有分布，这意味着没有对干扰w的概率分布进行任何假设。通过需要根据此类分布进行采样的量，关于w分布的信息仍然隐含存在。场景方法的这一特点使其对于无法获得可靠的干扰第一原理模型，但可以使用历史数据的应用非常有吸引力。 

2.2 带有测量的情景方法

在某些应用中，关于干扰 w 的在线信息可能是可用的。例如，尽管可能事先可以获得关于 w 分布的先验信息，但在做出决定时可能会进行一些直接测量。我们将具有测量的机会约束决策问题形式化为：

 其中 y = Hw 是扰动的线性测量，其中 H 是全行秩，表示条件概率。情景方法的直接应用，如 (3) 中的，将产生如下形式的确定性优化方程：

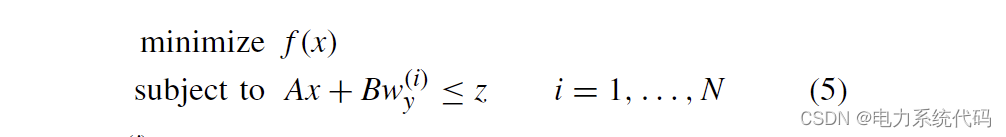
其中是由测量 y = Hw 确定的条件概率分布的样本 .

最后一种设置似乎抵消了实时操作场景方法的有效性，因为样本

只有在测量 y 可用后才需要生成。历史样本的使用使得这种新信息的整合变得困难。此外，由此产生的优化问题 (5) 仍然存在大量典型的冗余约束，这对直接使用场景方法进行快速实时决策提出了计算挑战。在下一节中，我们将展示如何通过样本的离线预处理阶段成功解决这两个问题，然后是在线测量驱动的决策步骤。 

三、 机会约束决策的一种快速方法

3.1 通过仿射变换进行近似调节

3.2 可行域的仿射变换

3.3 两阶段决策算法

四、算例——配电网

4.1 防止过电压的有功功率削减

4.2 数值模拟

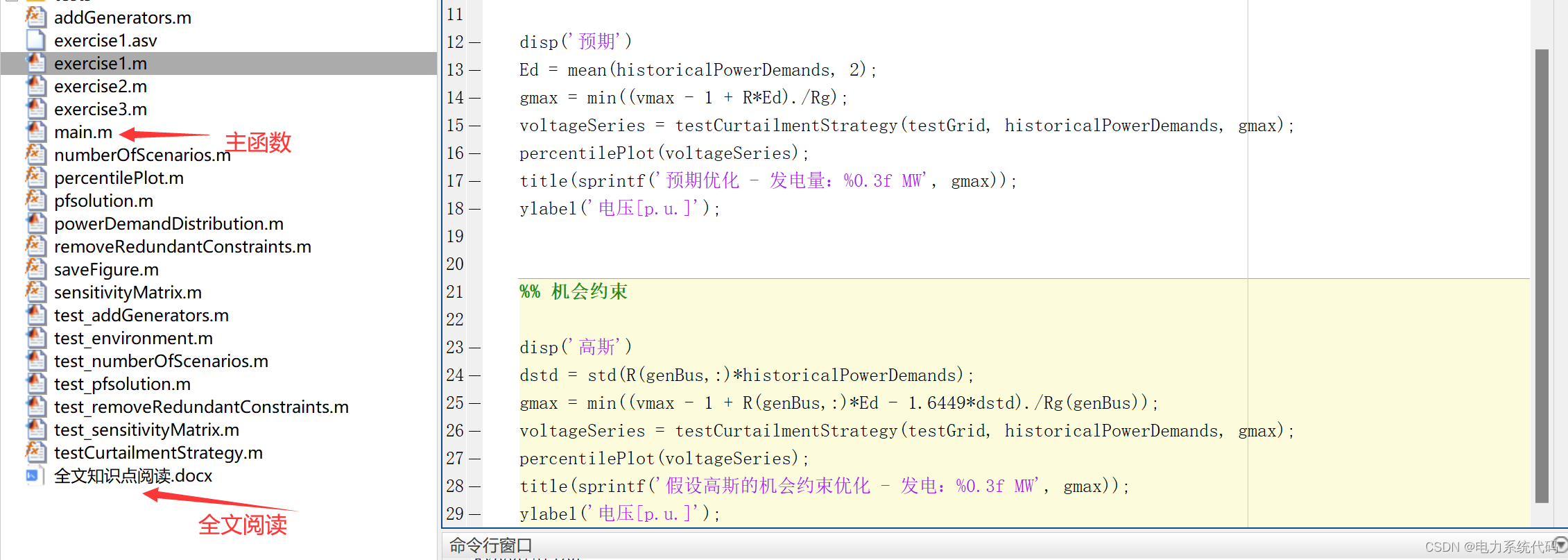
部分代码： 

%% ====鲁棒优化===========

disp('鲁棒')
gmax = (vmax - 1) / max(Rg);
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
title(sprintf('鲁棒优化——发电量：% 0.3f MW', gmax));
ylabel('电压 [p.u.]');

%% 预期

disp('预期')
Ed = mean(historicalPowerDemands, 2);
gmax = min((vmax - 1 + R*Ed)./Rg);
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
title(sprintf('预期优化 - 发电量：%0.3f MW', gmax));
ylabel('电压[p.u.]');


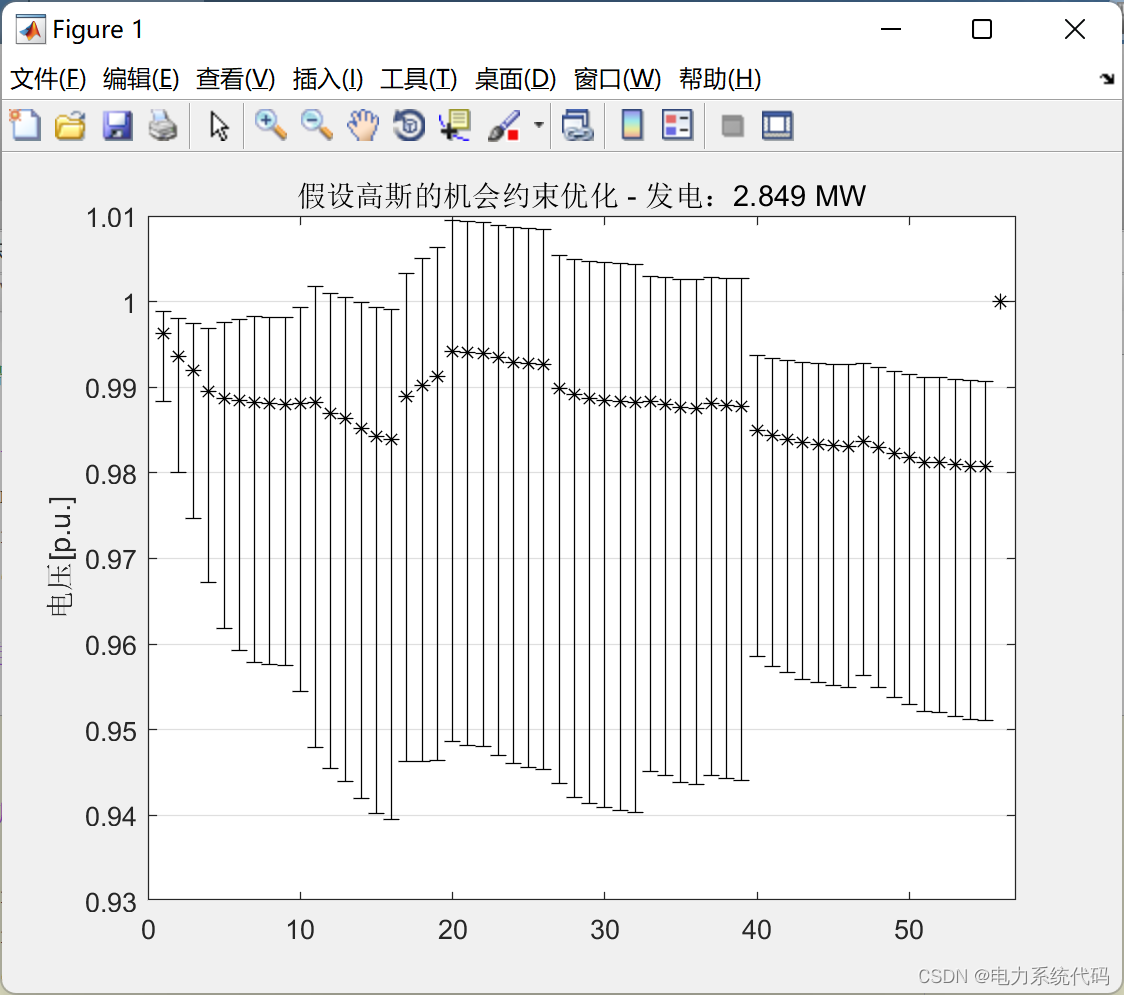
%% 机会约束

disp('高斯')
dstd = std(R(genBus,:)*historicalPowerDemands);
gmax = min((vmax - 1 + R(genBus,:)*Ed - 1.6449*dstd)./Rg(genBus));
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
title(sprintf('假设高斯的机会约束优化 - 发电：%0.3f MW', gmax));
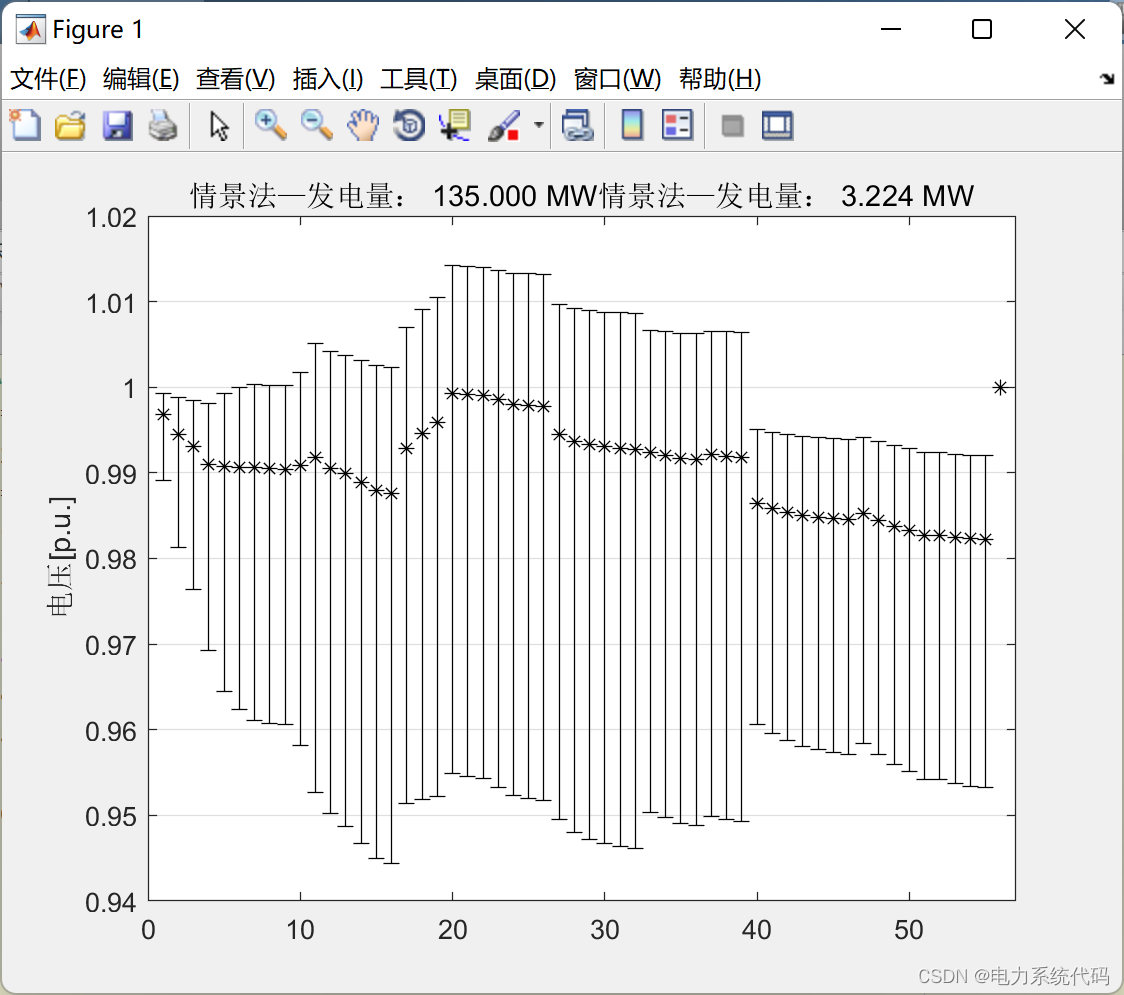
ylabel('电压[p.u.]');

 4.3 运行结果

           

 

 

5 Matlab代码实现