一、什么是多源最短路

我们之前了解到的dijkstra算法、SPFA算法、Bellman-Ford算法都是从起点到各个点的最短路，都是从一个源点出发的。因此，这些称作单源最短路。那么当我们想知道图中的任意两点的最短路的时候，我们可以使用n次单源最短路算法，但是这样做的话，就显得过于繁琐僵硬。
因此，为了解决多源最短路问题，世界上就出现了一种新的算法：Floyd算法。

二、Floyd算法

1、算法思路

我们还是延续我们之前的传统，先分析问题，而不是直接给出算法的步骤。

我们的目的是求出任意两个点之间的最短路。

那么我们首先思考的问题应该是用什么存储呢？
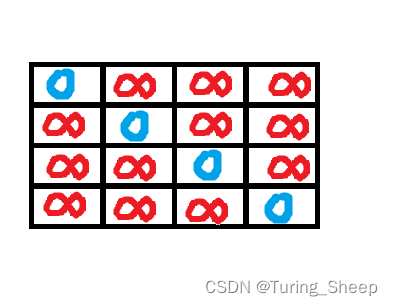
一个点通往n个点的最短路，我们一共要求n个点的。我们直接创建一个dis[N][N]。那么这个数组的初始化应该是什么样的呢？
我们知道，一个点到自身的最短距离肯定是0，即我们dis数组的对角线方向。除此之外，我们并不知道其余点之间的距离。因此我们讲dis数组的剩余部分初始化为正无穷。如下图所示：
在这里插入图片描述
接着，我们以下面的图为例，想一想我们如何求任意两点之间的最短路：

我们知道，在这个图里任意两点之间的最短路的路径上必经过图中的点。

那么我们与其去向最短路经过哪些点，不如反过来，我们想一想这些点在哪些最短路上。

那我们在顺着这个思路想一想，如果这个点在最短路上，那么这个点满足的条件是什么？根据我们前面推导单源最短路的文章中，我们了解到。我们的点如果在最短路上，那么我们用这个点去松弛最短路上的边的话，必定会松弛成功。

因此，我们要想知道一个点在哪些点的最短路上，我们只需要用这个点去松弛所有边。

我们举个例子吧：

比如上图中的F点。我们很容易看出来，A点想到G的话，必须过F，我们用F去松弛的话，AF边必定是会松弛成功的。因为在初始化的时候，这两个点之间的距离是正无穷。但AF之间的边权是常数。F点也有可能在A到I上，也就是说A到I的最短路有可能经过AF。如果我们假设AI之间的最短路就是过F的那一条的话，那么AI也是要经过AF的。而我们在用F松弛的时候，也确实松弛了这条边。另外，我们的F还会松弛成功FG和FI，这两个短边也有可能是某几个点之间的最短路上所经过的边。

因此，我们要想要知道所有点的最短路：

我们只需要让n个点都去松弛一遍所有的边，松弛过后，就能够确定这n个点都分别在哪几个点的最短路上，于是我们就知道了图中任意两点之间的最短路。

而这就是Floyd算法的算法逻辑。

2、算法模板

（1）问题：

在这里插入图片描述

（2）代码模板：

#include<iostream>
#include<cstring>
using namespace std;
const int N=210;
int dis[N][N];
int n,m,k;
void floyd()
{
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
            }
        }
    }
}
int main()
{
    cin>>n>>m>>k;
    memset(dis,0x3f,sizeof dis);
    for(int i=1;i<=n;i++)dis[i][i]=0;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        if(a!=b)
        dis[a][b]=min(dis[a][b],c);
    }
    floyd();
    for(int i=0;i<k;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        if(dis[a][b]>0x3f3f3f3f/2)puts("impossible");
        else printf("%d\n",dis[a][b]);
    }
    return 0;
}