c++--简单多状态动态规划问题

PS:以下代码均为C++实现

1.按摩师力扣

一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

注意：本题相对原题稍作改动

示例 1：

输入： [1,2,3,1]
输出： 4
解释：选择 1 号预约和 3 号预约，总时长 = 1 + 3 = 4。

示例 2：

输入： [2,7,9,3,1]
输出： 12
解释：选择 1 号预约、 3 号预约和 5 号预约，总时长 = 2 + 9 + 1 = 12。

示例 3：

输入： [2,1,4,5,3,1,1,3]
输出： 12
解释：选择 1 号预约、 3 号预约、 5 号预约和 8 号预约，总时长 = 2 + 4 + 3 + 3 = 12。

来源：力扣（LeetCode）

class Solution {
public:
    int massage(vector<int>& nums) 
    {
        int n=nums.size();
        if(n==0)//判断是否为空
            return 0;
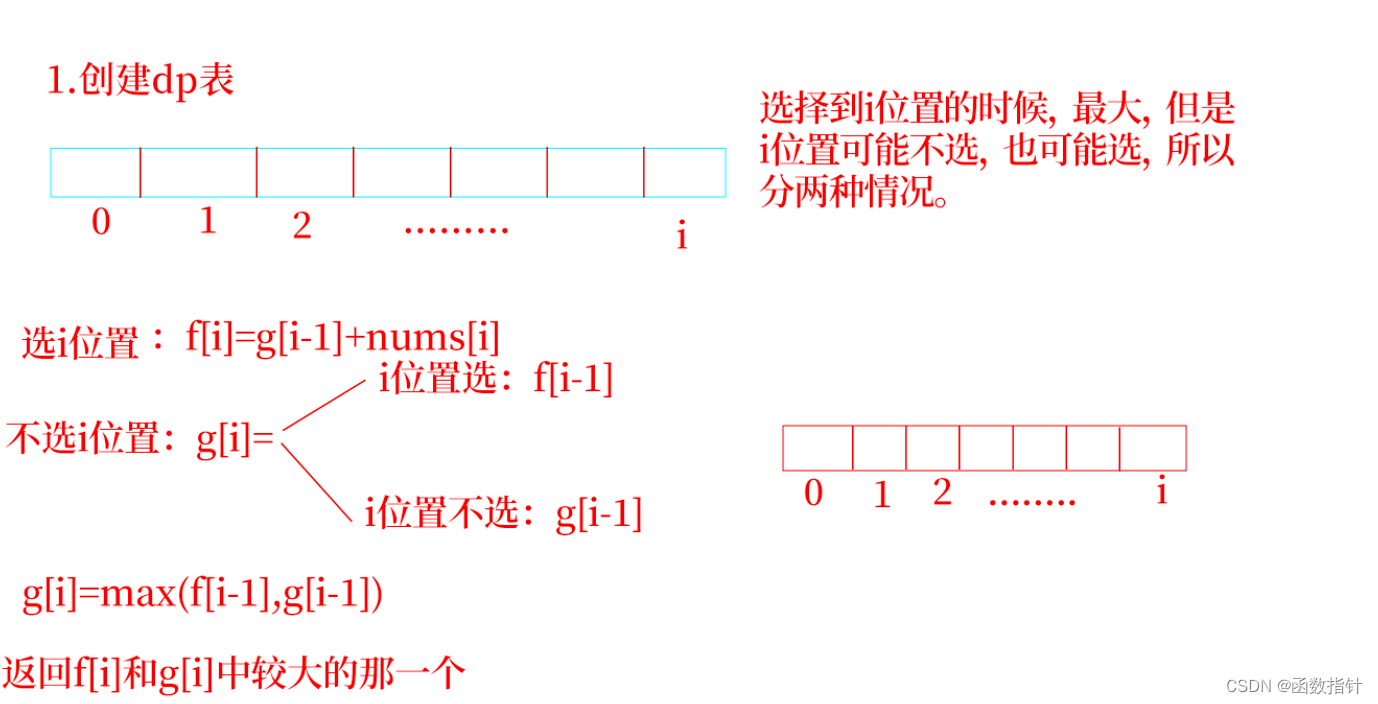
        vector<int> f(n);//创建dp表
        vector<int> g(n);
        g[0]=0;
        f[0]=nums[0];
        for(int i=1;i<n;i++)
        {
            f[i]=g[i-1]+nums[i];//状态转移方程
            g[i]=max(g[i-1],f[i-1]);//状态转移方程
        }
        return max(g[n-1],f[n-1]);//返回值
    }
};

2.打家劫舍2

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，今晚能够偷窃到的最高金额。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 3：

输入：nums = [1,2,3]
输出：3

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/house-robber-ii

class Solution {
public:
    int rob(vector<int>& nums) 
    {
        int n=nums.size();
        if(n==0||n==1||n==2)//判断是否越界
        {
            if(n==0) return 0;
            else if(n==1) return nums[0];
            else return max(nums[0],nums[1]);
        }
        return max(nums[0]+_rob(nums,2,n-2),_rob(nums,1,n-1));//返回最大的
    }
    int _rob(vector<int>& nums,int left,int right)//打家劫舍的子问题，即打家劫舍1的解答方案
    {
        int n=nums.size();
        vector<int> f(n);
        auto g=f;
        f[left]=nums[left];
        for(int i=left+1;i<=right;i++)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        return max(f[right],g[right]);
    }
};

3.删除并获得点数力扣

给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

示例 1：

输入：nums = [3,4,2]
输出：6
解释：
删除 4 获得 4 个点数，因此 3 也被删除。
之后，删除 2 获得 2 个点数。总共获得 6 个点数。

示例 2：

输入：nums = [2,2,3,3,3,4]
输出：9
解释：
删除 3 获得 3 个点数，接着要删除两个 2 和 4 。
之后，再次删除 3 获得 3 个点数，再次删除 3 获得 3 个点数。
总共获得 9 个点数。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/delete-and-earn

class Solution 
{
public:
    int deleteAndEarn(vector<int>& nums) 
    {
        vector<int> dp(10001);
        for(auto s:nums) dp[s]+=s;
        //可以删除为0的元素，节省空间
        vector<int> f(10001);
        auto g=f;
        f[0]=dp[0];
        for(int i=1;i<10001;i++)
        {
            f[i]=g[i-1]+dp[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        return max(f[10000],g[10000]);
        
    }
};

4.粉刷房子力扣

假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

示例 1：

输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

示例 2：

输入: costs = [[7,6,2]]
输出: 2

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/JEj789

class Solution {
public:
    int minCost(vector<vector<int>>& costs) 
    {
        int n=costs.size();
        vector<vector<int>> f(n+1,vector<int>(3));//创建dp表
        f[0][0]=0;
        for(int i=1;i<=n;i++)
        {
            f[i][0]=min(f[i-1][1],f[i-1][2])+costs[i-1][0]; //状态转移方程
            f[i][1]=min(f[i-1][0],f[i-1][2])+costs[i-1][1];
            f[i][2]=min(f[i-1][1],f[i-1][0])+costs[i-1][2];
        }


        return min(f[n][0],min(f[n][1],f[n][2]));//找最小的
    }
};

5.买卖股票的最佳时机含冷冻期力扣

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。

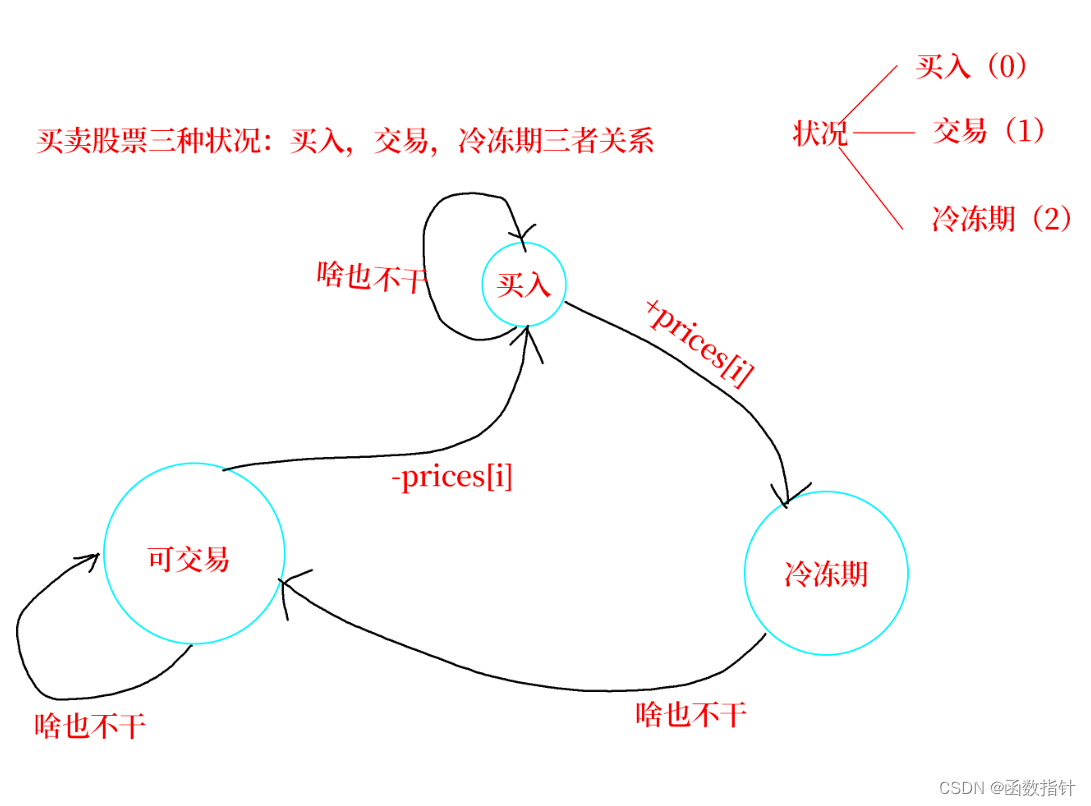
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

示例 2:

输入: prices = [1]
输出: 0

来源：力扣（LeetCode）

这道题和粉刷房子类似

class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int n=prices.size();
        vector<vector<int>> f(n+1,vector<int>(3));
        f[0][0]=-prices[0];
        for(int i=1;i<=n;i++)
        {
            f[i][0]=max(f[i-1][0],f[i-1][1]-prices[i-1]);
            f[i][1]=max(f[i-1][1],f[i-1][2]);
            f[i][2]=f[i-1][0]+prices[i-1];
        }
        return max(f[n][1],f[n][2]);
    }
};

6.买卖股票最佳时期含手续费力扣

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

示例 2：

输入：prices = [1,3,7,5,10,3], fee = 3
输出：6

来源：力扣（LeetCode）

//这道题并不难
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        int n=prices.size();
        vector<int> f(n);
        auto g=f;
        f[0]=-prices[0];
        for(int i=1;i<n;i++)
        {
            f[i]=max(f[i-1],g[i-1]-prices[i]);
            g[i]=max(g[i-1],f[i-1]+prices[i]-fee);
        }
        return g[n-1];
    }
};

7.买卖股票的最佳时期3 力扣

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天（股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

来源：力扣（LeetCode）

//这道题可以不用看，直接看下一道题
class Solution {
    const int INF=0x3f3f3f3f;
public:
    int maxProfit(vector<int>& prices) 
    {
        int n=prices.size();
        vector<vector<int>> f(n,vector<int>(2+1,-INF));
       
        auto g=f;
        f[0][0]=-prices[0];
        g[0][0]=0;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=2;j++)
            {
                f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
                g[i][j]=g[i-1][j];
                if(j>=1)
                {
                    g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int ret=0;
        for(int i=0;i<=2;i++)
        {
            ret=max(ret,g[n-1][i]);
        }
        return ret;
    }
};

8.买卖股票的最佳时期4 力扣

给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

来源：力扣（LeetCode）

class Solution {
    const int INF=0x3f3f3f3f;//避免越界，INT_MAX的一半
public:
    int maxProfit(int k, vector<int>& prices) 
    {
        int n=prices.size();
        vector<vector<int>> f(n,vector<int>(k+1,-INF));//创建dp表
        k=min(k,n/2);//简化循环时间
        auto g=f;
        f[0][0]=-prices[0];//初始化
        g[0][0]=0;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=k;j++)
            {
                f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);//状态转移方程
                g[i][j]=g[i-1][j];//确定最大
                if(j>=1)
                {
                    g[i][j]=max(g[i][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int ret=0;
        for(int i=0;i<=k;i++)
        {
            ret=max(ret,g[n-1][i]);//找最大值
        }
        return ret;
    }
};