论文信息
题目:NeRF-SLAM: Real-Time Dense Monocular SLAM with Neural Radiance Fields
作者:Antoni Rosinol, John J. Leonard, Luca Carlone
代码:https://github.com/ToniRV/NeRF-SLAM
来源:arxiv
时间:2022
Abstract
我们提出了一种新颖的几何和光度 3D 映射流程,用于从单目图像进行准确、实时的场景重建。
为了实现这一目标,我们利用了密集单目 SLAM 和实时分层体积神经辐射场的最新进展。
我们的见解是,密集单目 SLAM 通过提供准确的姿态估计和具有相关不确定性的深度图,提供正确的信息来实时拟合场景的神经辐射场。
通过我们提出的基于不确定性的深度损失,我们不仅实现了良好的光度精度,而且还实现了很高的几何精度。
事实上,我们提出的流程比竞争方法实现了更好的几何和光度精度(PSNR 提高了 179%,L1 深度提高了 86%),同时实时工作并且仅使用单目图像。
Introduction
我们的见解是,拥有一个密集的单目 SLAM 管道,可以输出接近完美的姿态估计,以及密集的深度图和不确定性估计,为动态构建场景的神经辐射场提供正确的信息。我们的实验表明,这确实是可能的,并且与其他方法相比,我们可以在更短的时间内实现更准确的重建。
贡献 我们提出了第一个场景重建流程,结合了密集单目 SLAM 和分层体积神经辐射场的优点。我们的方法从图像流构建准确的辐射场,不需要姿势或深度作为输入,并且实时运行。我们在单目方法的Replica数据集上实现了最先进的性能
Related Work
Dense SLAM
实现密集 SLAM 的主要挑战是
(i)由于要估计的深度变量的剪切量而导致计算复杂性
(ii)处理模糊或缺失的信息来估计场景的深度,例如无纹理表面或别名图像。
从历史上看,
第一个问题已经通过解耦姿态和深度估计来绕过。例如,DTAM [19] 通过使用与稀疏 PTAM [13] 相同的范例来实现密集 SLAM,该范例首先以解耦的方式跟踪相机姿态,然后跟踪深度。
第二个问题通常也可以通过使用提供显式深度测量的 RGB-D 或激光雷达传感器或简化深度估计的立体相机来避免。
最近关于密集SLAM的研究在这两个方面取得了令人印象深刻的成果。
为了减少深度变量的数量,CodeSLAM [4] 优化了从图像推断深度图的自动编码器的潜在变量。通过优化这些潜在变量,问题的维数显着降低,而所得的深度图仍然密集。
Tandem [14] 能够通过使用预训练的 MVSNet 式神经网络进行单目深度估计来仅使用单目图像重建 3D 场景,然后通过执行帧到模型光度跟踪来解耦姿势/深度问题。
Droid-SLAM [31] 表明,通过采用最先进的密集光流估计架构 [30] 来解决视觉里程计问题,可以在各种具有挑战性的数据集(例如Euroc [5] 和 TartanAir [34] 数据集),Droid-SLAM 通过使用下采样深度图来避免维数问题,随后使用学习的上采样算子进行上采样。
Rosinol 等人 [23] 进一步表明,密集单目 SLAM 可以通过边缘协方差对密集 SLAM 中估计的深度进行加权,然后将它们融合在体积表示中,从而重建场景的忠实 3D 网格。生成的网格在几何上是准确的,但由于 TSDF 表示的限制,它们的重建缺乏光度细节并且不完全完整。
我们的方法受到 Rosinol 等人 [23] 的工作的启发,其中我们将体积 TSDF 替换为分层体积神经辐射场作为我们的地图表示。通过使用辐射场,我们的方法实现了光度精确的地图并提高了重建的完整性,同时还允许同时优化姿势和地图
Neural Radiance Fields(NeRF)
虽然使用一个大型 MLP 的普通 NeRF 方法需要数小时的训练才能收敛,但几位作者表明,较小的 MLP 与 3D 空间数据结构相结合来划分场景,可以显着提高速度。
特别是,NGLOD [27]建议在体积网格中使用微小的 MLP,从而实现更快的重建,但不太实时。 Plenoxels [40] 通过使用球谐函数参数化方向编码进一步提高了速度,同时绕过了 MLP 的使用。最后,Instant-NGP [17] 表明,通过基于哈希的场景分层体积表示,可以实时训练神经辐射场。
Mono-SDF [41] 表明,用于单目图像深度和法线估计的最先进的深度学习模型提供了有用的信息,可以显着提高辐射场重建的收敛速度和质量。
我们的工作通过使用密集 SLAM 提供的信息来利用这些见解,该信息估计姿势和密集深度图。我们还利用密集 SLAM 输出本质上是概率性的事实,并使用当前方法中通常被丢弃的信息来对监控信号进行加权以适应辐射场。
SLAM with NeRFs
神经辐射场研究的另一个重要轴是消除其对部分已知相机姿势的依赖。这对于构建 NeRF 特别有吸引力,而无需处理数据来获取图像的相机姿势,这项任务通常很长,通常使用 COLMAP [25] 完成。
我们的工作利用了最近在密集单目 SLAM(Droid-SLAM [31])、概率体积融合(Rosinol 等人[23])和基于哈希的分层体积辐射场(Instant-NGP [17])方面的工作,实时估计场景的几何和光度图,无需深度图像或姿势。
Methodology
我们方法的主要思想是使用密集单目 SLAM 的输出来监督神经辐射场。
密集单目 SLAM 可以估计密集深度图和相机姿势,同时还提供深度和姿势的不确定性估计。有了这些信息,我们就可以训练一个具有由深度边际协方差加权的密集深度损失的辐射场。通过使用密集 SLAM 和辐射场训练的实时实现,并通过并行运行它们,我们实现了实时性能。
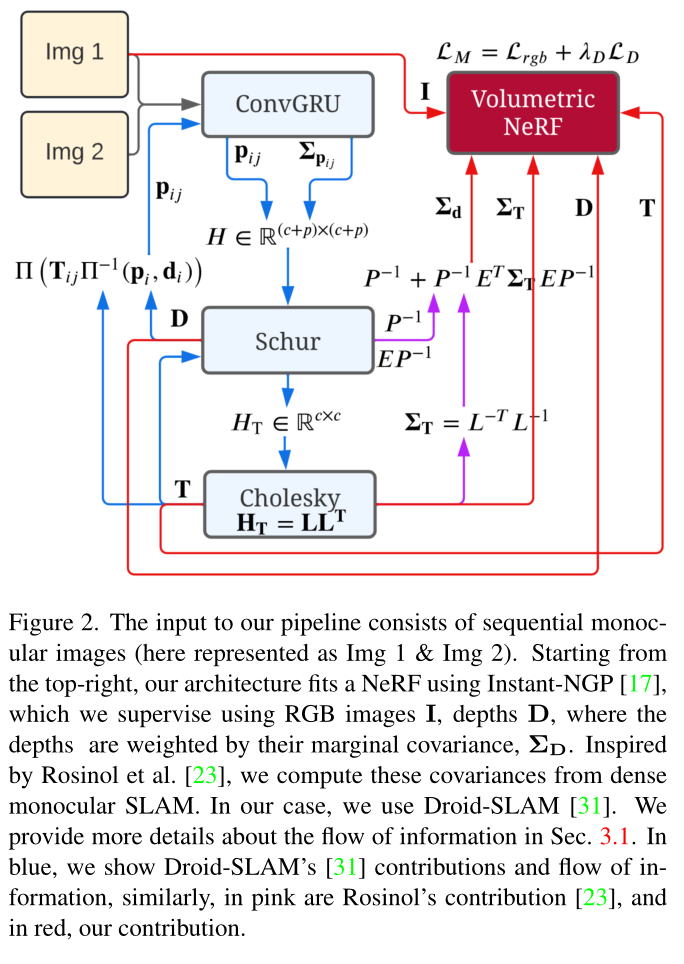
图 2 显示了我们管道中的信息流。我们现在解释我们的架构,从我们的跟踪前端(第 3.1 节)开始,然后是我们的映射后端(第 3.2 节)。
Tracking:Dense SLAM with Covariances
我们使用 Droid-SLAM [31] 作为跟踪模块,它为每个关键帧提供密集的深度图和姿势。
从图像序列开始,Droid-SLAM 首先使用与 Raft [30] 类似的架构计算帧对 i 和 j 之间的密集光流 p i j p_{ij} pij。
Raft 的核心是一个卷积 GRU(图 2 中的 ConvGRU),给定帧对之间的相关性和当前光流 pij 的猜测,计算新的流 p i j p_{ij} pij 以及每个光流的权重 Σ p i j Σ_{p_{ij}} Σpij流量测量。
通过这些流量和权重作为测量值,DroidSLAM 解决了密集束调整 (BA) 问题,其中 3D 几何形状被参数化为每个关键帧的一组逆深度图。这种结构的参数化导致了一种解决密集 BA 问题的极其有效的方法,通过将方程组线性化为熟悉的摄像机/深度箭头状块稀疏 Hessian H ∈ R ( c + p ) × ( c + p ) H \in \mathbb{R}^{(c+p)×(c+p)} H∈R(c+p)×(c+p),可以将其表示为线性最小二乘问题,其中 c c c和 p p p是相机和点的维数
为了解决线性最小二乘问题,我们采用Hessian矩阵的Schur补来计算简化的相机矩阵HT,
它不依赖于深度,并且具有更小的
R
c
×
c
\mathbb{R}^{c\times c}
Rc×c维数。通过对
H
T
=
L
L
T
H_T = LL^T
HT=LLT 进行 Cholesky 分解(其中 L 是下三角 Cholesky 因子),然后通过前后替换求解姿势 T,可以解决由此产生的关于相机位姿的较小问题。
如图 2 底部所示,给定这些姿势 T,我们可以求解深度 d。此外,给定姿势 T 和深度 D,Droid-SLAM 建议计算诱导光流,并将其作为初始猜测再次馈送到 ConvGRU 网络,如图 2 左侧所示,其中 Π 和 Π−1 ,是投影和反投影函数。图2中的蓝色箭头显示了跟踪环路,对应于Droid-SLAM。
我们进一步计算密集深度图和 Droid-SLAM 姿势的边际协方差(图 2 中的紫色箭头)。为此,我们需要利用 Hessian 的结构,我们将其按如下方式进行块划分
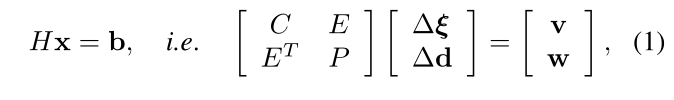
where
H
H
H is the Hessian matrix,
b
b
b the residuals,
C
C
C is the block camera matrix, and
P
P
P is the diagonal matrix corresponding to the inverse depths per pixel per keyframe. We represent by
∆
ξ
∆ξ
∆ξ the delta updates on the lie algebra of the camera poses in
S
E
(
3
)
SE(3)
SE(3), while ∆d is the delta update to the per-pixel inverse depths.
E
E
E is the camera/depth off-diagonal Hessian’s block matrices, and
v
v
v and
w
w
w correspond to the pose and depths residuals.
密集深度
Σ
d
Σ_d
Σd 和位姿
Σ
T
Σ_T
ΣT 的边际协方差,如下所示:
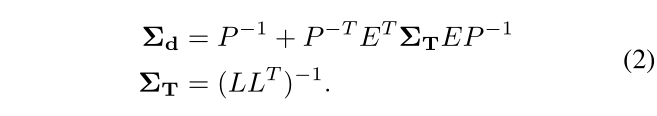
Mapping:probalilistic Volumetric NeRF
考虑到每个关键帧的密集深度图,可以对我们的神经体积进行深度监督。不幸的是,深度图由于其密度而非常嘈杂,因为即使是无纹理区域也被赋予了深度值。
图 3 显示,密集单目 SLAM 生成的点云噪声特别大,并且包含较大的异常值(图 3 中的顶部图像)。在给定这些深度图的情况下监督我们的辐射场可能会导致有偏差的重建

考虑到不确定性损失,我们将映射损失表示为:
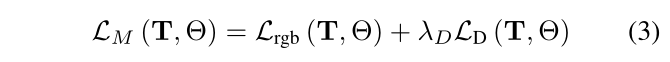
给定超参数 λD 平衡深度和颜色监督(我们将 λD 设置为 1.0),我们将姿势 T 和神经参数 θ 最小化。特别是,我们的深度损失由下式给出:
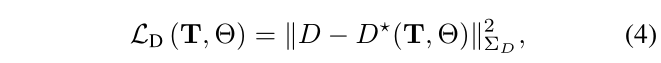
其中
D
∗
D^*
D∗是渲染的深度,
D
、
Σ
D
D、Σ_D
D、ΣD是跟踪模块估计的密集深度和不确定性。
我们渲染深度
D
∗
D^*
D∗作为预期的光线终止距离,每个像素的深度是通过沿像素光线采样 3D 位置、评估样本 i 处的密度
σ
i
σ_i
σi 以及对所得密度进行 alpha 合成来计算的,与标准体积渲染类似:
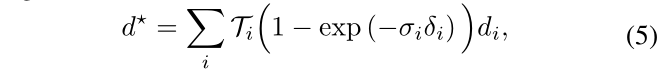
其中
d
i
d_i
di 是样本 i 沿射线的深度,
δ
i
=
d
i
+
1
−
d
i
δ_i = d_{i+1} − d_i
δi=di+1−di是连续样本之间的距离。
σ
i
σ_i
σi 是体积密度,通过评估样本 i 的 3D 世界坐标处的 MLP 生成。最后,
T
i
T_i
Ti是沿光线直到样本 i 的累积透射率,定义为
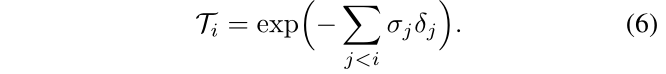
我们的颜色损失的定义如原始 NeRF [16] 中所示:
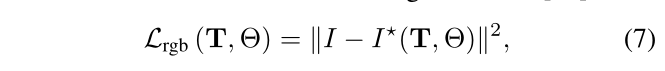
其中
I
∗
I^*
I∗ 是渲染的彩色图像,与深度图像类似,通过使用体积渲染进行合成。每个像素的每种颜色同样是通过沿像素的光线采样并通过 alpha 合成所得的密度和颜色来计算的:
∑
i
T
i
(
1
−
exp
(
−
σ
i
δ
i
)
)
c
i
\sum_{i} \mathcal{T}_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}
∑iTi(1−exp(−σiδi))ci,其中
T
i
\mathcal{T}_{i}
Ti 是公式 (6) 中的透射率。
c
i
\mathbf{c}_{i}
ci 是 MLP 估计的颜色。对于给定样本 i,同时估计密度
δ
i
\delta_{i}
δi 和颜色
c
i
\mathbf{c}_{i}
ci。
Architecture
我们的管道由跟踪Tracking线程和映射Mapping线程组成,两者都实时并行运行。
跟踪线程持续最小化关键帧活动窗口的 BA 重投影误差。
映射线程始终优化从跟踪线程接收到的所有关键帧,并且没有活动帧的滑动窗口。
当跟踪管道生成新的关键帧时,这些线程之间的唯一通信发生。在每个新关键帧上,跟踪线程将当前关键帧的姿势及其各自的图像和估计的深度图以及深度的边际协方差发送到映射线程。仅将跟踪线程的滑动优化窗口中当前可用的信息发送到映射线程。跟踪线程的活动滑动窗口最多由 8 个关键帧组成。一旦前一个关键帧和当前帧之间的平均光流高于阈值(在我们的例子中为 2.5 像素),跟踪线程就会生成新的关键帧。
映射线程还负责渲染以实现重建的交互式可视化。
Result
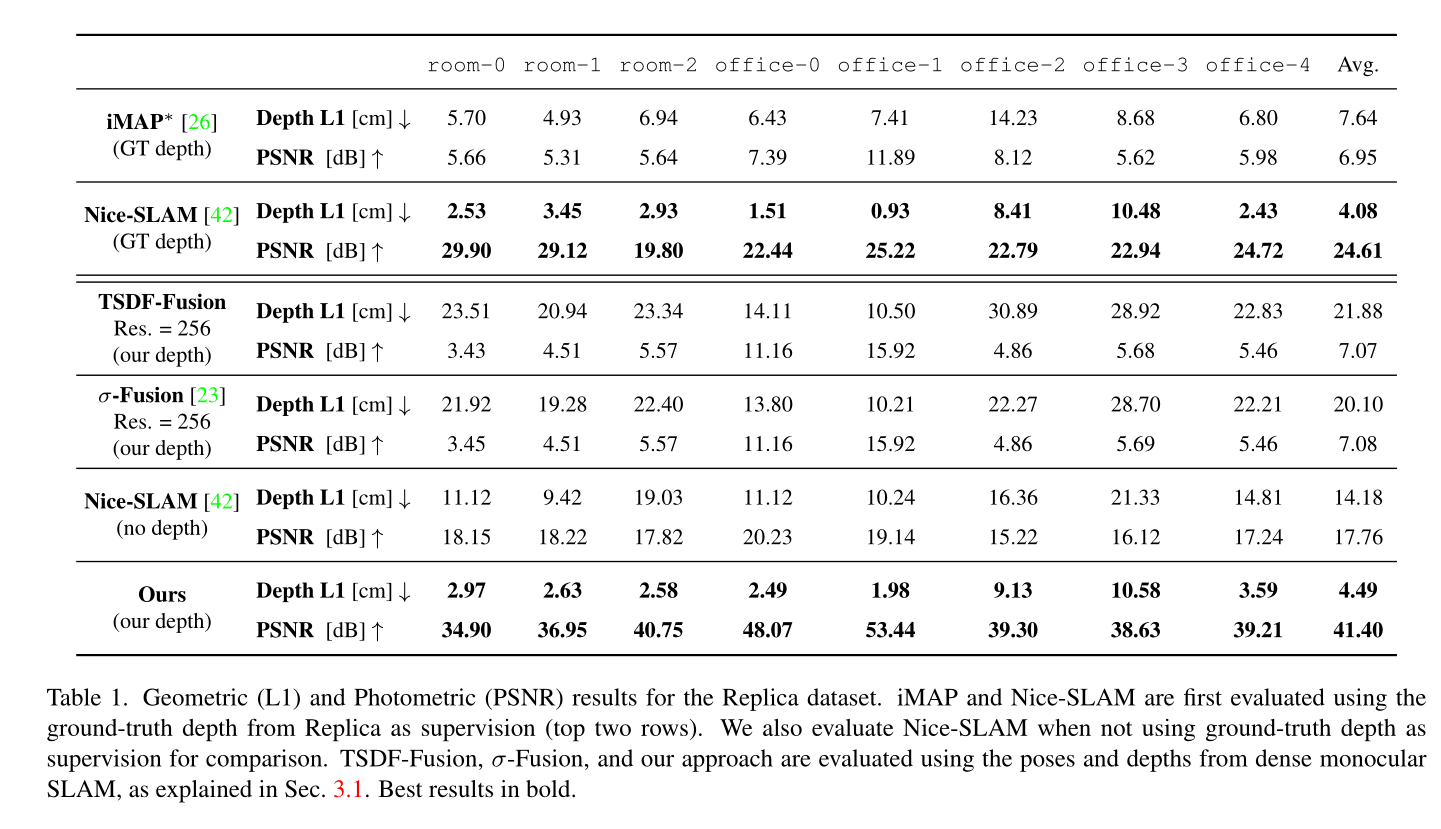

Conclusion
我们证明,密集单目 SLAM 为从随意拍摄的单目视频中构建场景的 NeRF 表示提供了理想的信息。来自密集 SLAM 的估计姿态和深度图,通过其边际协方差估计进行加权,为优化基于分层散列的体积神经辐射场提供了理想的信息源。通过我们的方法,用户可以实时生成场景的光度和几何精确重建。
未来的工作可以利用我们的方法来扩展度量语义 SLAM [24] 的定义,该定义通常只考虑几何和语义属性,通过构建光度准确的表示形式。
除了度量语义 SLAM 之外,我们的方法还可以用作高级场景理解的映射引擎,例如用于构建 3D 动态场景图 [2,21,22]。