在进行均值滤波和方框滤波时，其邻域内每个像素的权重是相等的。在高斯滤波中，会将中心点的权重值加大，远离中心点的权重值减小，在此基础上计算邻域内各个像素值不同权重 的和。

基本原理

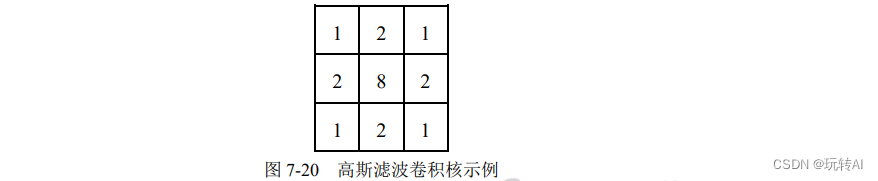
在高斯滤波中，卷积核中的值不再都是 1。例如，一个 3×3 的卷积核可能如图 7-20 所示：

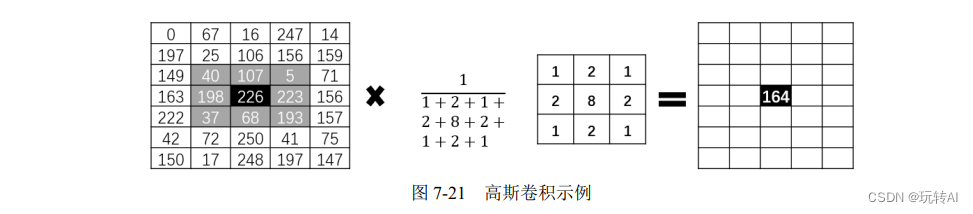
在图 7-21 中，针对最左侧的图像内第 4 行第 3 列位置上像素值为 226 的像素点进行高斯卷积，其运算规则为将该点邻域内的像素点按照不同的权重计算和。

在实际计算时，使用的卷积核如图 7-22 中的卷积核所示。

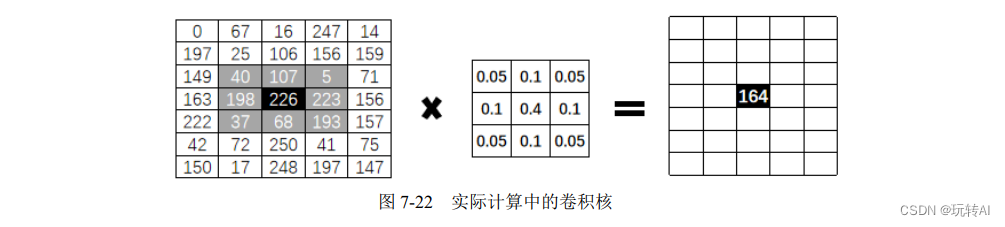
使用图 7-22 中的卷积核，针对第 4 行第 3 列位置上的像素值为 226 的像素点进行高斯滤
波处理，计算方式为：

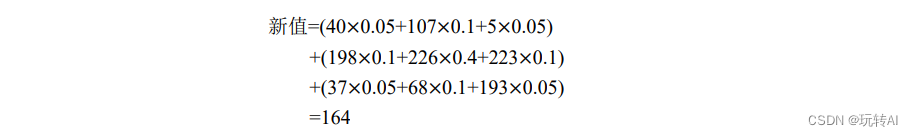
在实际使用中，高斯滤波使用的可能是不同大小的卷积核。例如，图 7-23 中分别是 3×3、5×5、7×7 大小的卷积核。在高斯滤波中，核的宽度和高度可以不相同，但是它们都必须是奇数。

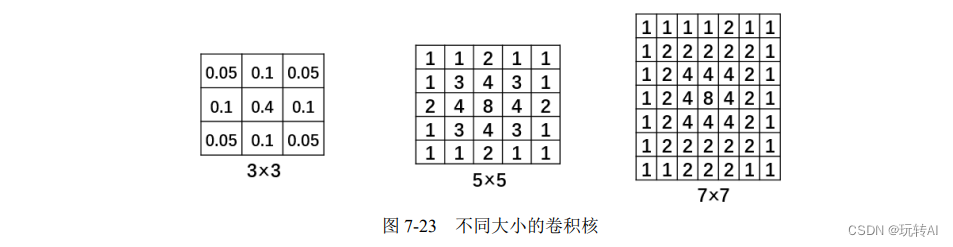
每一种尺寸的卷积核都可以有多种不同形式的权重比例。

例如，同样是 5×5 的卷积核，可能是图 7-24 中所示的两种不同的权重比。

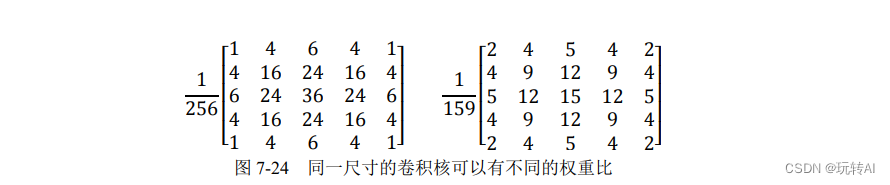
在不同的资料中，卷积核有多种不同的表示方式。它们可能如图 7-23 所示写在一个表格内，也可能如图 7-24 所示写在一个矩阵内。

在实际计算中，卷积核是归一化处理的，这种处理可以表示为图 7-23 最左侧的小数形式的卷积核，也可以表示为如图 7-24 所示的分数形式。
也要注意，在一些资料中，给出的卷积核并没有进行归一化，这时的卷积核可能表示为图 7-23 中间和右侧所示的卷积核，这样的卷
积核是为了说明问题用的，实际使用时往往需要进行归一化。严格来讲，使用没有进行归一化处理的卷积核进行滤波，得到的结果往往是错误的。

在 OpenCV 中，实现高斯滤波的函数是 cv2.GaussianBlur()，该函数的语法格式是：

dst = cv2.GaussianBlur( src, ksize, sigmaX, sigmaY, borderType )

式中：
 dst 是返回值，表示进行高斯滤波后得到的处理结果。

 src 是需要处理的图像，即原始图像。它能够有任意数量的通道，并能对各个通道独立
处理。图像深度应该是 CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F 中的一种。

 ksize 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度。
需要注意，滤波核的值必须是奇数。

 sigmaX 是卷积核在水平方向上（X 轴方向）的标准差，其控制的是权重比例。

例如，图 7-25 中是不同的 sigmaX 决定的卷积核，它们在水平方向上的标准差不同。

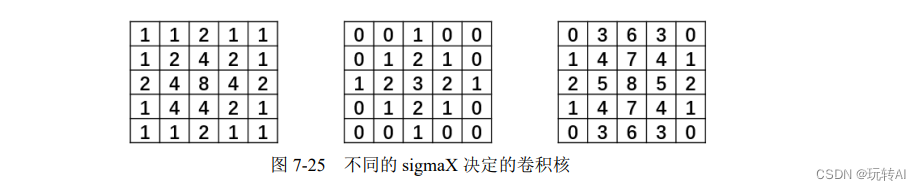
sigmaY 是卷积核在垂直方向上（Y 轴方向）的标准差。如果将该值设置为 0，则只采用sigmaX 的值；如果 sigmaX 和 sigmaY 都是 0，则通过 ksize.width 和 ksize.height 计算得到。
其中：
 sigmaX = 0.3×[(ksize.width-1)×0.5-1] + 0.8
 sigmaY = 0.3×[(ksize.height-1)×0.5-1] + 0.8

 borderType 是边界样式，该值决定了以何种方式处理边界。一般情况下，不需要考虑该值，直接采用默认值即可。

在该函数中，sigmaY 和 borderType 是可选参数。sigmaX 是必选参数，但是可以将该参数设置为 0，让函数自己去计算 sigmaX 的具体值。

官方文档建议显式地指定 ksize、sigmaX 和 sigmaY 三个参数的值，以避免将来函数修改后可能造成的语法错误。

当然，在实际处理中，可以显式指定 sigmaX 和 sigmaY 为默认值 0。因此，函数 cv2.GaussianBlur()的常用形式为：

dst = cv2.GaussianBlur( src, ksize, 0, 0 )

实验:对噪声图像进行高斯滤波，显示滤波的结果。

代码如下:

import cv2
o=cv2.imread("lenaNoise.png")
r=cv2.GaussianBlur(o,(5,5),0,0)
cv2.imshow("original",o)
cv2.imshow("result",r)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果:其中左图是原始图像，右图是高斯滤波后的处理
结果图像。