0 上周回顾

上周完成了VelocityGAN的重现和学习.
认识到了利用判别器网络对于常规网络进行约束是很一种很高效的设计思路.

1 本周论文背景简述

这篇论文: 《Multiscale Data-Driven Seismic Full-Waveform Inversion With Field Data Study》
2021年底的论文, 发表于TGRS 2022. 其实也算比较新的一篇味道很纯粹的DL-FWI.
本周阅读的论文是从多尺度 (multi-scale) 角度来训练DL-FWI. 在之前几个月刚接触DL-FWI的时候, 遇到过类似的设计思路.
除了模型这道主菜外, 这篇论文也加了一些味道奇特的作料:

数据方面: 他提出了风格迁移的速度模型.
实验方面: 他找到了一个现场数据, 并对其进行了实验.

2 模型架构

作者认为, 地震波传播的运动学非常复杂, 这使得FWI成为一个复杂的问题. 而多尺度方法的目的就是将复杂和反演分解为一系列相对更简单的反演过程.
本文中, 作者将反演工作划分为:

低分辨率 (低频的) 反演和
高分辨率 (高频) 反演

两部分, 前者的反演结果是一个分辨率比较低的速度模型, 他将作为第二部分的高分辨率反演的材料之一.

低分辨率FWI反演的结构如下图所示:
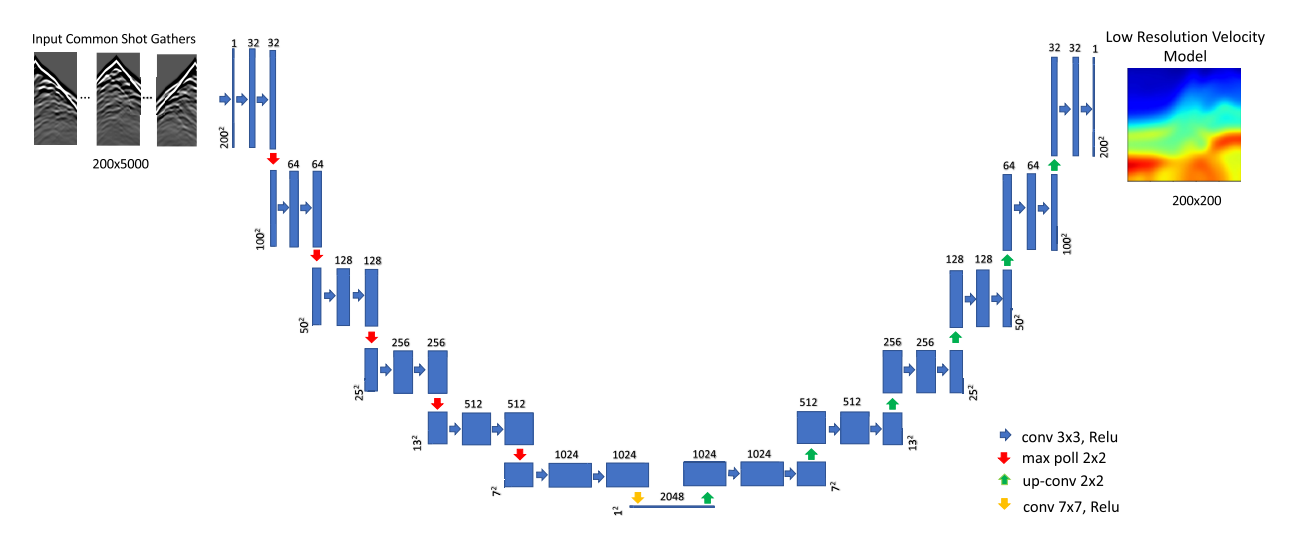
在这里插入图片描述
这个结构类似于InversionNet, 但是却要比其更简洁化:

网络的输入部分不再通过卷积进行降维, 虽然他输入的是一个 $200\times5000$ 的观测数据, 但是实际在输入到网络中时会通过额外的采样插值操作将其压缩为 $200\times200$ , 这个步骤在多数高级编程语言中只是一行代码的问题. 这样的结果使得网络输入和输出是同维度大小的.
下采样不再依靠卷积完成, 而是直接通过经典的最大池化完成.

最后需要留意, 它仍是编-解码网络, 最终编码仍是 $1\times1$ 的 $2048$ 通道的高维数据.
高分辨率反演如下图所示:
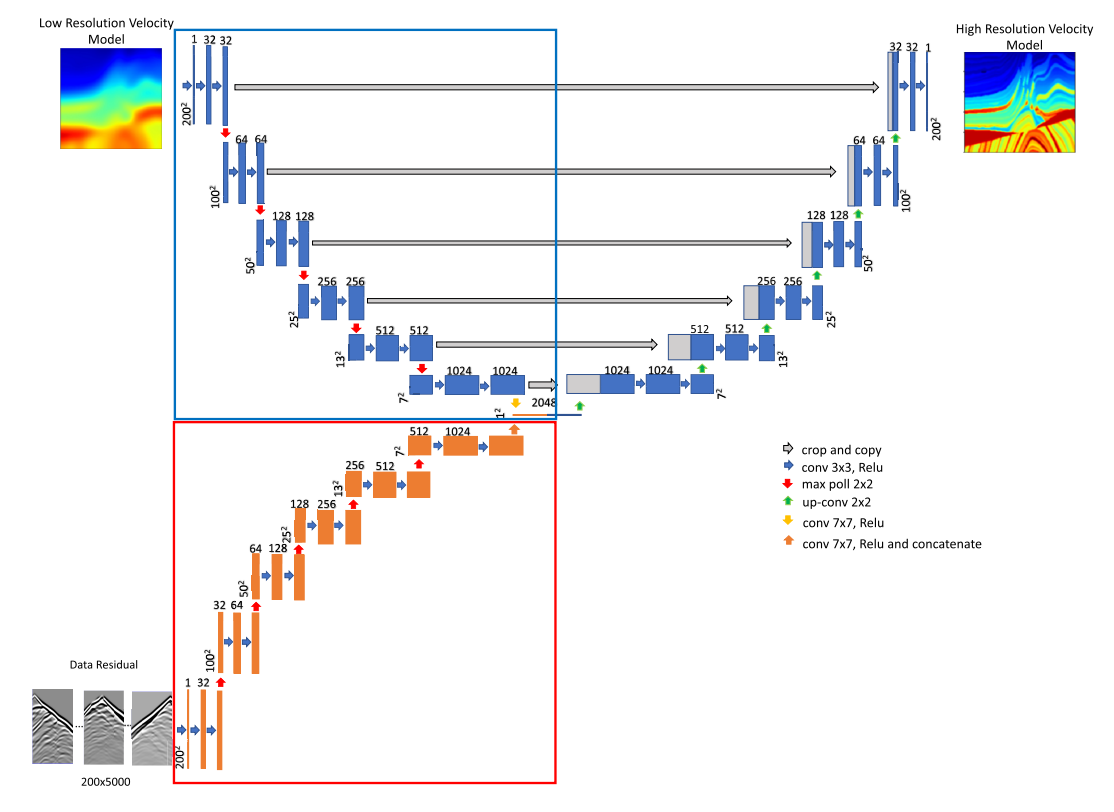
在这里插入图片描述
高分辨率速度模型体现了多尺度网络的特点.
首先, 编码器包含两个部分, 模型部分 (蓝色框表示, 是UNet网络) 和数据部分 (红框表示, 常规CNN). 模型部分编码器的输入数据是低分辨率反演网络预测的低分辨率速度模型; 而数据部分编码器的输入数据是一个残差观测数据. 残差观测数据是:
预测的低分辨率速度模型再度经过正演得到观测数据 减去 真实观察数据 而得到的.
论文中公式10说明了这个来源:

$\mathbf{d}_i^{\text{diff}} = \mathbf{d}_i^{\text{pre}} - \mathbf{d}_i^{\text{true}} \tag{1}$

如此设置也是有原因的:
地震波主要分为例如反射波, 透射波, 直达波等, 它们每个都遵循不同的波传播路径和机制. 而地层图像的不同频率成分反映的波形也是不一样的:

低频 (低分辨率) 信息主要由直达波表征, 低分辨率反演大多数时候只能表达观察数据中直达波解释的地层构造;
而高频 (高分辨率) 信息可以解释更细节且复杂的反射波和投射波等较为细节的波形, 这些波能观察到一些细节反射面的变化.

作者认为这两者的信息较为独立, 如果强行在一个体系下进行时较难找到通用解, 于是进行两阶段分别拟合.

最后, “为什么高分辨网络采用 $\mathbf{d}_i^{\text{diff}}$ ?”:
因为预测的低分辨率速度模型再度正演 所得到就是一个主要由直达波和传输波解释的观测地震数据, 通过与真实观察数据作差就能得到主要由反射波等其他高频信息解释的地震观测信息. 这个信息可以使得高分辨率反演网络专注于拟合高频信息, 符合其定位.

这个网络的训练并非全局地forward和back propagation, 而是局部性的, 分段性的. 作者认为, 对于这种多尺度网络, 简单地全局性训练可能会导致不平衡的收敛, 意味着网络的一部分将主导训练而不是另一部分. 而两步代替训练法将会很好缓解这个问题.

固定红框的数据部分编码器, 训练图中UNet部分的网络结构. 属于 [低频->高频] 的图像处理过程. 这个过程中, 低频经验将融入到解码器中.
固定蓝框的模型部分编码器, 训练图中红框的CNN编码器. 输入[观测数据->速度模型] 的FWI过程, 新的观测数据残差将更新速度模型以获得高频信息.

最后, 观察到网络的细节架构. 两个编码器的首次相汇是在压缩为 $1\times1$ 的图像之后的通道融合, 这次融合就图中来看不像是求和而更像是通道的简单连接 (1024+1024). 而且, 似乎在固定了一个编码器之后, 另一个编码器也会进行正常传递, 但是不求导. 因为编码器的末端需要使用到两个编码器压缩的高维向量信息. 所以至少, 固定了B\编码器后, B编码器也要至少传递1次, 直到获得压缩后的高维信息为止, 然后再去训练A编码器.
另外, 图中的蓝框和红框内的网络结构是基本一致的, 唯有的不同是在解码器时期, 对于它俩的信息使用是不同的, 前者因为是UNet, 需要注意Skip connection的问题.

-一些训练参数-
低分辨率反演网络
训练集: 测试集 = 65000:2000
Batch size = 10
Adam优化器
训练50轮
Loss直接采用MSE

高分辨率反演网络
训练集: 测试集 = 65000:2000
Batch size = 10
Adam优化器
训练20轮
Loss直接采用MSE

总结来看, 架构的基本结构可以简化为下面这张草稿:
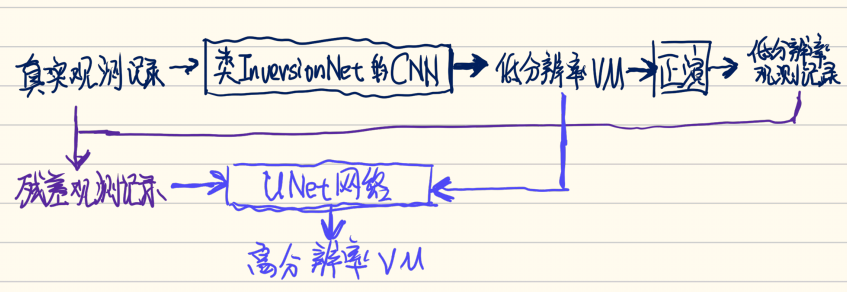
在这里插入图片描述

3 风格化速度模型

风格化速度模型本质上采用了风格迁移的思想, 他将我们常见的日常拍摄照片作为 “内容” 源, 而地下层次化的地层构造作为 “风格” 源, 并它俩进行融合的过程, 具体可见下面的网络结构:
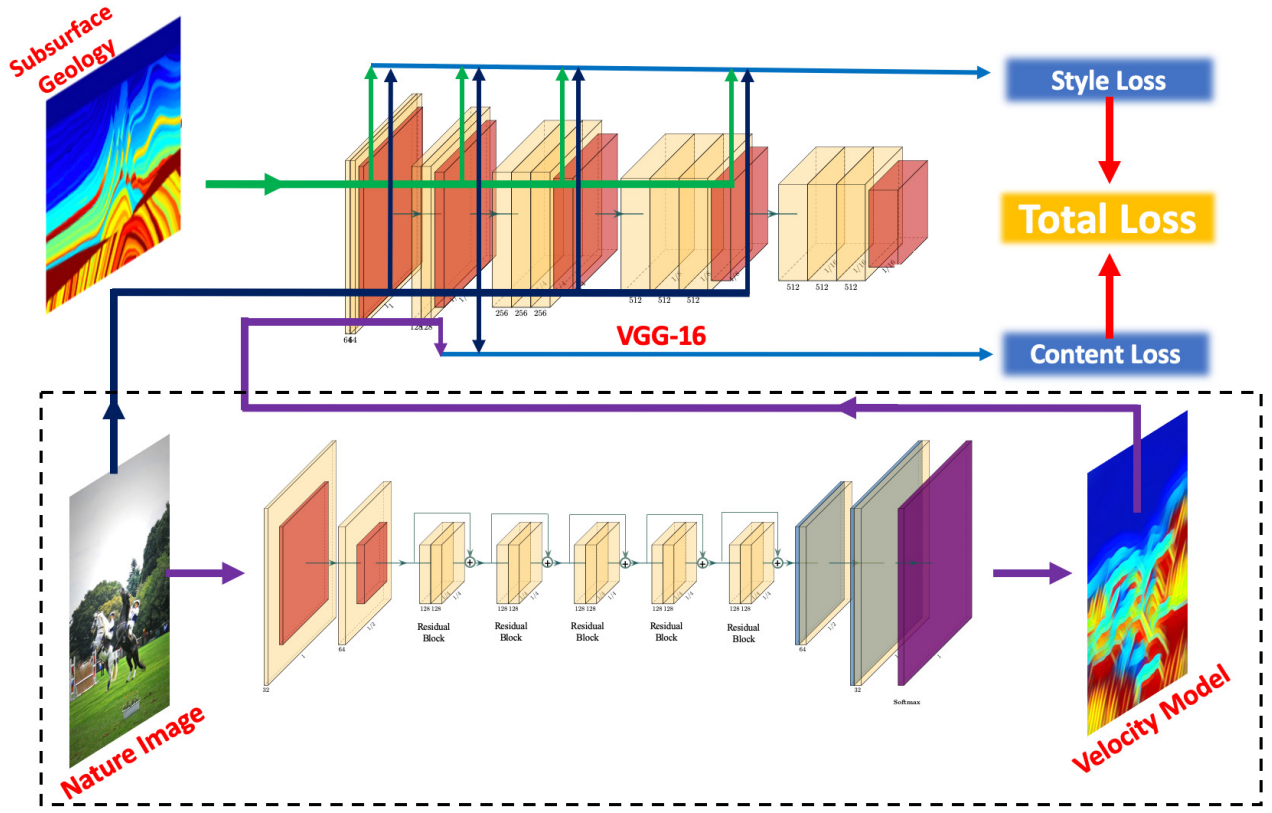
在这里插入图片描述
下侧是一个采用了残差结构的编-解码网络, 它的目的是将自然图像转化为我们目标的风格化速度模型. 但是这个目标的拟合过程无法仅仅依靠这个简单的编解码网络, 而需要上侧的VGG-16网络来辅助.
这个VGG是一个已有的比较著名的网络:

VGG，又叫VGG-16，顾名思义就是有16层，包括13个卷积层和3个全连接层，是由Visual Geometry Group组的Simonyan和Zisserman在文献《Very Deep Convolutional Networks for Large Scale Image Recognition》中提出卷积神经网络模型，该模型主要工作是证明了增加网络的深度能够在一定程度上影响网络最终的性能。其年参加了ImageNet图像分类与定位挑战赛，取得了在分类任务上排名第二，在定位任务上排名第一的优异成绩。
原文链接：https://blog.csdn.net/qq_45998041/article/details/114626473

VGG-16在此处的目的是收集特征, 从而用来结算Loss信息, 它在整个训练过程是被固定的, 不会进行逆向传播, 它是预训练好的 (文章中没有介绍是如何雨荨来拿的).
具体来说, 地层图像会经过VGG-16网络, 并被我们主观地提取前四层的激活函数ReLU1_2, ReLU2_2, ReLU3_3, ReLU4_4分析得到的特征; 自然图像则只提取ReLU2_2的特征;
这些特征最终被转化为Gram矩阵, 地层图像 (风格来源图像) $y_s$ 的特征Gram矩阵在论文中表示为 $G_j(y_s)$ ; 自然图像 $y_c$ (内容来源图像) 的特征Gram矩阵在论文中表示为 $G_j(y_c)$ ; 预测的合成图像 $y$ 的特征Gram矩阵在论文中表示为 $G_j(y)$
论文中给出了公式:
$l_{\text{style}} = \sum_{j \in S} \frac{1}{U_j}\|G_j(y) - G_j(y_s)\|^2 \tag{2}$
$l_{\text{content}} = \sum_{j \in C} \frac{1}{U_j}\|G_j(y) - G_j(y_c)\|^2 \tag{3}$
$l_{\text{trans}} = \alpha_{\text{style}} l_{\text{style}} +\alpha_{\text{content}} l_{\text{content}}\tag{4}$
其中 $S$ 和 $C$ 都是对应的VGG-16在风格重建中使用到特征层, 我可以猜测 $S\in[$ ReLU1_2, ReLU2_2, ReLU3_3, ReLU4_4 $]$ , $C\in[$ ReLU2_2 $]$ . 然后每层算Gram差值的二范数, 最终逐层求和.
公式告诉了我们, 合成的图像 $y$ 在具体到算不同的loss时 (Style or Content), 会一同参与到对方的特征层进行特征提取, 最终一并求差值.

BUT
这篇论文有点不对劲, 在论文的其余两个地方, 这个说法又有点不一样的 !

首先, 我们可以看图片, 图中Style Loss好像是 地层风格图像 $y_s$ 与 自然内容图像 $y_c$ 相互计算得到的, 好像没有预测合成图像 $y$ 什么事耶? 这与上述列出的公式2不符.
然后, 图下方的解释文字:

Style loss is defined as the Gram matrix difference between the features of the natural images and the subsurface geology in relu1_2, relu2_2, relu3_3, and relu4_4 layers. Content loss is the MSE loss between the features of the natural images and the subsurface geology in the relu2_2 layer.

这里在介绍Content Loss的时候明确说明了这个损失是natural images与subsurface geology的提取特征的MSE. 首先不说这个过程似乎依旧没有预测合成图像 $y$ 什么事, 更甚的是, 这段对图的解释说明好像和图中Content Loss中的流程线本身都不符合.
希望读过这篇论文的小伙伴能在评论出指出我是否有哪里理解错了?
如果真的论文有误, 我更倾向于支持公式的做法, 因为预测合成数据 $y$ 本身参与到loss计算才有意义.

言归正传, 最终制作出合成速度模型之后还并未结束, 因为这个时候我们的速度模型还并不满足地下的一些特征. 我们需要通过具有线性增加值的一维速度模型背景来进行基本的加权:
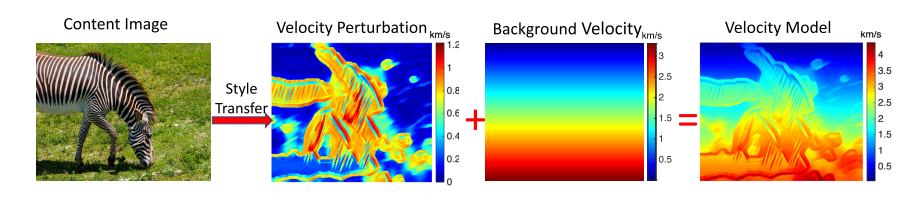
在这里插入图片描述
公式如下:
$v_{\text {com }}=\beta_{\text {pert }} v_{\text {pert }}+\left(1-\beta_{\text {pert }}\right) v_{\text {back }} \tag{5}$ .
随着逐渐降低 $\beta_\text{pert}$ 的值, 下述图像逐步从左边向右侧变化.

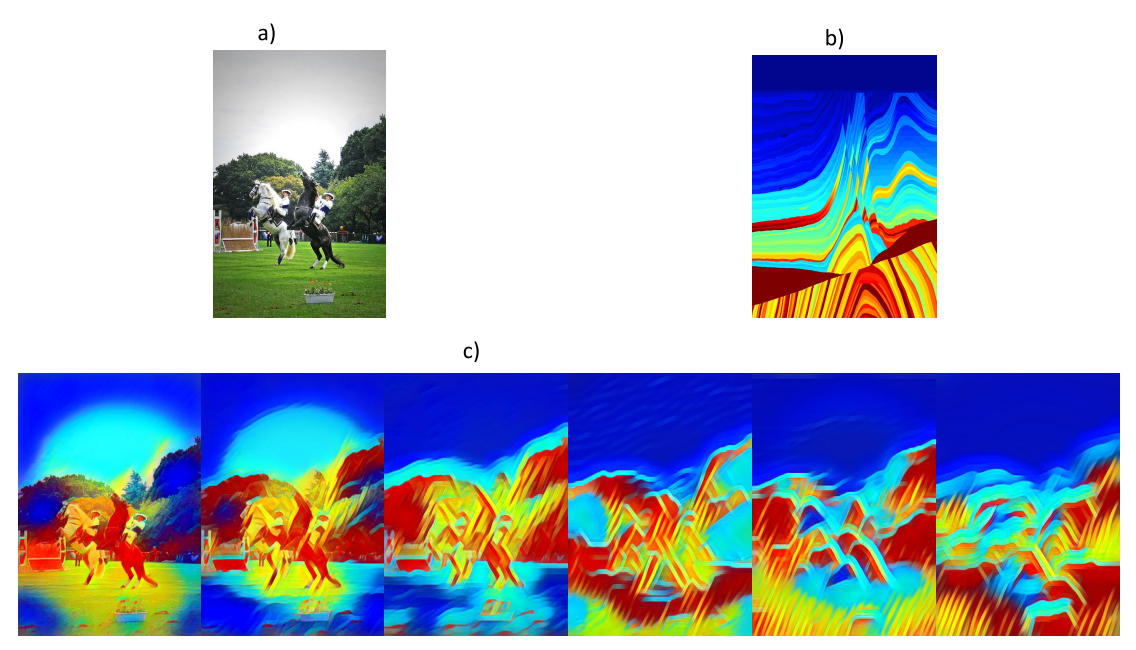
这些自然图像大多来自COCO数据集的67000张图片. 主要的速度模型样貌如下:
在这里插入图片描述
虽然轮本身并没有公布这些合成后的数据集, 但是OpenFWI团队在自己网站上给出了这个数据集的下载版本: https://openfwi-lanl.github.io/docs/data.html (其中的Style-A为强平滑版本, Style-B为弱平滑版本, 后者难度更大)

4 训练与实际数据的测试

关于正演的设置, 这里有些参数.
首先速度模型本身描述的是 $2$ km $\times2$ km的地下环境.
正演网格的间距为 $10$ m, 设置了 $10$ 个炮点, 每个炮间距为 $200$ m, $200$ 个接收器间隔 $10$ m放置. 震源频率为 $15$ Hz. 这些参数将作用于合成速度模型来正演.
额外需要注意一个问题, 即关于平滑性的问题. 低分辨率反演的时候我们会对速度模型进行6~10的高斯滤波; 而高分辨反演并不是说不会进行平滑, 实际上也会, 会进行偏差值为0~5的平滑, 会很弱但是也有.

此外作者还在经典的Marmousi速度模型上进行了测试.
然后还引入了一个比较陌生的Overthrust速度模型. 似乎是一个现实的速度模型. 详见论文: 《Three dimensional SEG/EAEG models—An update》
总的来说, Overthrust速度模型会比Marmousi好些, Marmousi的反演效果在浅层部分区域比较好, 但是仍然有些地方的褶皱反演是异常的.

最后, 原作者在2-D Gulf of Mexico真实数据集中进行了测试. 并且与两种基于物理手段的反演方法进行了比较, 分别是WT (走时反演) 和传统FWI.
通过观察文中他给的正演参数, 这个真实数据非常宽:
这是一个宽为 $8.125$ km, 纵向方向为 $1.5$ km的二维工区.
网络间隔是 $6.25$ m.
为了与合成数据一致, 这里还是采用 $10$ 个炮点, 炮点之间间距 $375$ m.
安排了 $480$ 个间隔 $12.5$ m的接收器. 初步可以推断观测数据的宽度为 $480$
但是采样时长没有透露, 但是看图片的尺寸, 估计最终都要下采样到 $480$ , 构成方形.
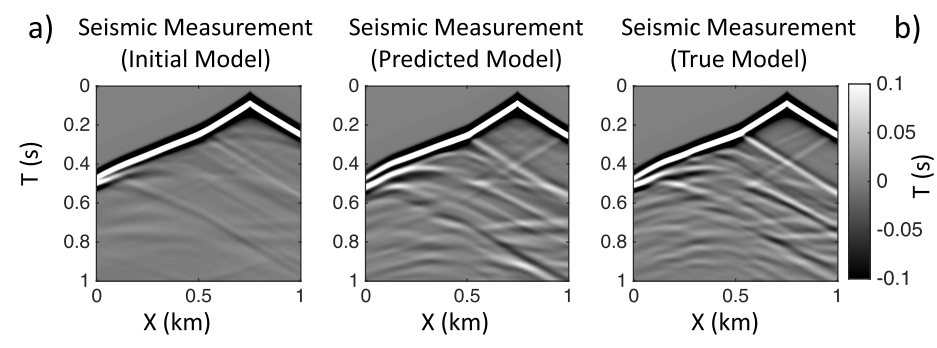
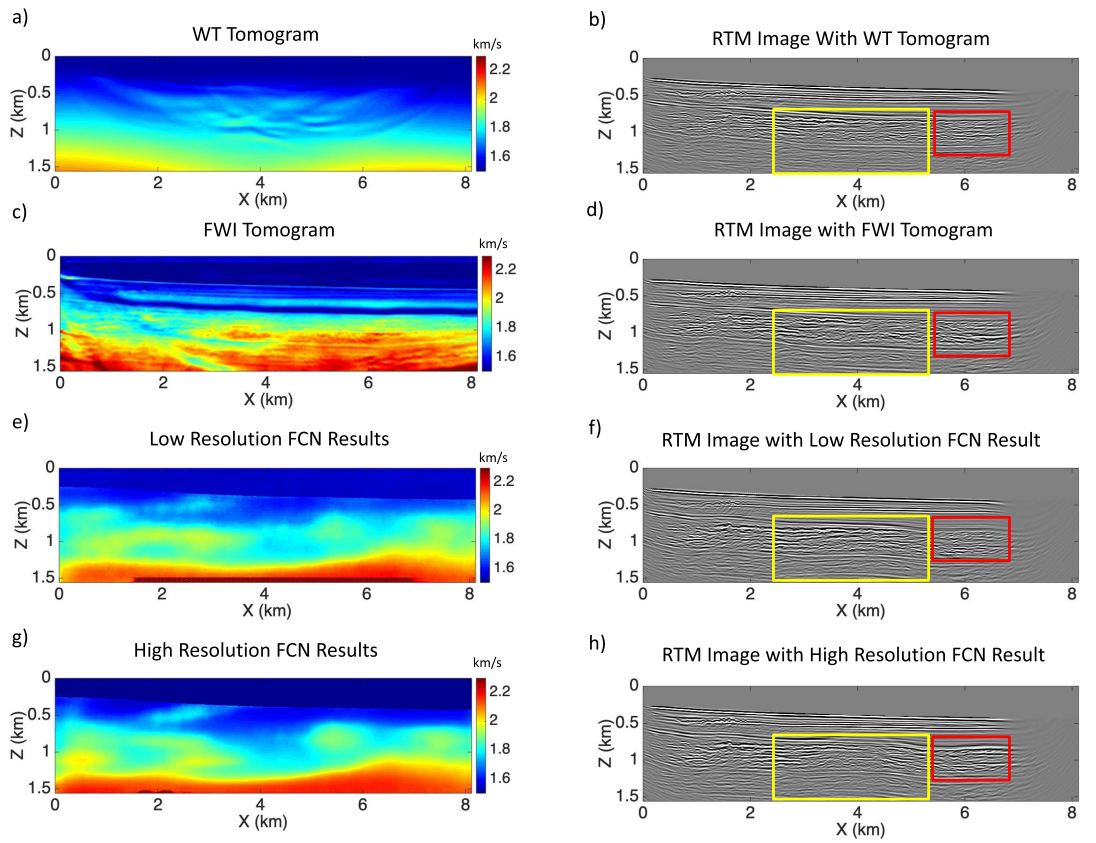
在这里插入图片描述
作者这里引入WT的目的是为了和低分辨率反演来进行对比, 因为实际上它俩都是针对观测信息中的传输波, 都只能反演出浅层的区域以及模糊的速度模型. 到具体的操作层面, 我们会提前将WT和低分辨率反演的观测地震数据的反射波静默以消除干扰, 保证公平的比较. 当然, 这个静默并非完美, 仍然会残留一些反射波,这些信息会被低分辨率反演捕捉到, 因此我们的低分辨率反演相比于WT还是能刻画出一些深层的反射事件.

后续作者还刻画了基于每个预测的速度模型和观测数据来刻画的RTM图像来共同进行对比.
在这里插入图片描述

5 存在的一些问题

这篇论文其实不连续地读了三次, 第一次在一个月前, 当时只了解了大概.
后续认真读了一次, 发现了文章在风格迁移的Loss的说明上存在的诡异之处.
于是反复揣摩作者的含义看是不是自己理解错了, 这是第三次.
最后我还是感觉诡异…
风格迁移的Loss函数的说明过程在图, 图示, 公式中都不太一致, 也许是我理解的问题? 但是确实没有哪理解有误吧…要说哪个部分合理, 我觉得公式的解释更合理.

实际要运用的话, 其实这里的bug倒又无关痛痒了, 因为风格化迁移后的数据有现成开源的, 而且很多 ( $95$ GB), 不用咱们自己去生成. 我觉得, 只需要大概明白这里的风格迁移思路, 即风格源和内容源之间的关系和VGG网络的特征提取就好了. 对我来说, 最重要的还是两阶段的多尺度网络架构.

6 总结和下一步工作

速度模型可以不完全拘泥于严格的层次化图像, 它可以很抽象. 这样的观点将速度模型扩大到更广泛的图像层次.
FWI应用在深度网络中的时候, 可以将其反演的波信息抽象出来, 简单的直达/传输波可以作为第一步, 而复杂的反射波可以作为第二步. 并且前一步也能为第二步提供先验信息 (初始速度模型).
多尺度 (Multi-scale) 思想可以用在DL-FWI, 分布拟合就好.

下步工作是再看些论文, 来敲定主要思路.