目录
1.什么是stl
2.六大组件-容器-序列式容器-C++98 string
3.六大组件-容器-序列式容器-C++98 vector
4.六大组件-容器-序列式容器-C++98 list
5.六大组件-容器-序列式容器-C++98 deque
6.六大组件-容器-序列式容器-C++11 array
7.六大组件-容器-序列式容器-C++11 forward_list
8.六大组件-容器-关联式容器-map/set/multimap/multiset
9.六大组件-容器-关联式容器-二叉树搜索树
10.六大组件-容器-关联式容器-AVL树
11.六大组件-容器-关联式容器-红黑树
12.六大组件-容器-底层为哈希结构-unordered_map/set/multimap/multiset
13.六大组件-容器-底层为哈希结构-哈希
14.六大组件-迭代器
15.六大组件-算反
16.六大组件-适配器
17.六大组件-仿函数
18.六大组件-空间配置
1.什么是stl?
与类型无挂
与具体的数据结构无关
算法非常灵活,有些算法只是一个框架(半成品),算法具体做什么事情,需要用户来定制
2.六大组件-容器-序列式容器-C++98 string
2.1接口一览
namespace cl
{
//模拟实现string类
class string
{
public:
typedef char* iterator;
typedef const char* const_iterator;
//默认成员函数
string(const char* str = ""); //构造函数
string(const string& s); //拷贝构造函数
string& operator=(const string& s); //赋值运算符重载函数
~string(); //析构函数
//迭代器相关函数
iterator begin();
iterator end();
const_iterator begin()const;
const_iterator end()const;
//容量和大小相关函数
size_t size();
size_t capacity();
void reserve(size_t n);
void resize(size_t n, char ch = '\0');
bool empty()const;
//修改字符串相关函数
void push_back(char ch);
void append(const char* str);
string& operator+=(char ch);
string& operator+=(const char* str);
string& insert(size_t pos, char ch);
string& insert(size_t pos, const char* str);
string& erase(size_t pos, size_t len);
void clear();
void swap(string& s);
const char* c_str()const;
//访问字符串相关函数
char& operator[](size_t i);
const char& operator[](size_t i)const;
size_t find(char ch, size_t pos = 0)const;
size_t find(const char* str, size_t pos = 0)const;
size_t rfind(char ch, size_t pos = npos)const;
size_t rfind(const char* str, size_t pos = 0)const;
//关系运算符重载函数
bool operator>(const string& s)const;
bool operator>=(const string& s)const;
bool operator<(const string& s)const;
bool operator<=(const string& s)const;
bool operator==(const string& s)const;
bool operator!=(const string& s)const;
private:
char* _str; //存储字符串
size_t _size; //记录字符串当前的有效长度
size_t _capacity; //记录字符串当前的容量
static const size_t npos; //静态成员变量(整型最大值)
};
const size_t string::npos = -1;
//<<和>>运算符重载函数
istream& operator>>(istream& in, string& s);
ostream& operator<<(ostream& out, const string& s);
istream& getline(istream& in, string& s);
}
2.2 深浅拷贝
浅拷贝:拷贝出来的目标对象的指针和源对象的指针指向的内存空间是同一块空间。其中一个对象的改动会对另一个对象造成影响。
深拷贝:深拷贝是指源对象与拷贝对象互相独立。其中任何一个对象的改动不会对另外一个对象造成影响。
2.3resize 和reserve
resize既分配了空间,也创建了对象,可以通过下标访问。当resize的大小
reserve只修改capacity大小,不修改size大小,resize既修改capacity大小,也修改size大小。
3.六大组件-容器-序列式容器-C++98 vector
3.1接口一览
namespace cl
{
//模拟实现vector
template<class T>
class vector
{
public:
typedef T* iterator;
typedef const T* const_iterator;
//默认成员函数
vector(); //构造函数
vector(size_t n, const T& val); //构造函数
template<class InputIterator>
vector(InputIterator first, InputIterator last); //构造函数
vector(const vector<T>& v); //拷贝构造函数
vector<T>& operator=(const vector<T>& v); //赋值运算符重载函数
~vector(); //析构函数
//迭代器相关函数
iterator begin();
iterator end();
const_iterator begin()const;
const_iterator end()const;
//容量和大小相关函数
size_t size()const;
size_t capacity()const;
void reserve(size_t n);
void resize(size_t n, const T& val = T());
bool empty()const;
//修改容器内容相关函数
void push_back(const T& x);
void pop_back();
void insert(iterator pos, const T& x);
iterator erase(iterator pos);
void swap(vector<T>& v);
//访问容器相关函数
T& operator[](size_t i);
const T& operator[](size_t i)const;
private:
iterator _start; //指向容器的头
iterator _finish; //指向有效数据的尾
iterator _endofstorage; //指向容器的尾
};
}
3.2 vector的扩容机制
新增元素:Vector通过一个连续的数组存放元素,如果集合已满,在新增数据的时候,就要分配一块更大的内存,将原来的数据复制过来,释放之前的内存,在插入新增的元素;
对vector的任何操作,一旦引起空间重新配置,指向原vector的所有迭代器就都失效了 ;
初始时刻vector的capacity为0,塞入第一个元素后capacity增加为1;
不同的编译器实现的扩容方式不一样,VS2015中以1.5倍扩容,GCC以2倍扩容。
3.3 vector的迭代器失效
迭代器失效就是指迭代器底层对应指针所指向的空间被销毁了,而指向的是一块已经被释放的空间,如果继续使用已经失效的迭代器,程序可能会崩溃。
使用迭代器时,永远记住一句话:每次使用前,对迭代器进行重新赋值。
3.4 vector和list的区别
vector和数组类似,拥有一段连续的内存空间,并且起始地址不变。
因此能高效的进行随机存取,时间复杂度为o(1);
但因为内存空间是连续的,所以在进行插入和删除操作时,会造成内存块的拷贝,时间复杂度为o(n)。
另外,当数组中内存空间不够时,会重新申请一块内存空间并进行内存拷贝。
list是由双向链表实现的,因此内存空间是不连续的。
只能通过指针访问数据,所以list的随机存取非常没有效率,时间复杂度为o(n);
但由于链表的特点,能高效地进行插入和删除。
如果需要高效的随机存取,而不在乎插入和删除的效率,使用vector;
如果需要大量的插入和删除,而不关心随机存取,则应使用list。
4.六大组件-容器-序列式容器-C++98 list
4.1接口一览
namespace cl
{
//模拟实现list当中的结点类
template<class T>
struct _list_node
{
//成员函数
_list_node(const T& val = T()); //构造函数
//成员变量
T _val; //数据域
_list_node<T>* _next; //后继指针
_list_node<T>* _prev; //前驱指针
};
//模拟实现list迭代器
template<class T, class Ref, class Ptr>
struct _list_iterator
{
typedef _list_node<T> node;
typedef _list_iterator<T, Ref, Ptr> self;
_list_iterator(node* pnode); //构造函数
//各种运算符重载函数
self operator++();
self operator--();
self operator++(int);
self operator--(int);
bool operator==(const self& s) const;
bool operator!=(const self& s) const;
Ref operator*();
Ptr operator->();
//成员变量
node* _pnode; //一个指向结点的指针
};
//模拟实现list
template<class T>
class list
{
public:
typedef _list_node<T> node;
typedef _list_iterator<T, T&, T*> iterator;
typedef _list_iterator<T, const T&, const T*> const_iterator;
//默认成员函数
list();
list(const list<T>& lt);
list<T>& operator=(const list<T>& lt);
~list();
//迭代器相关函数
iterator begin();
iterator end();
const_iterator begin() const;
const_iterator end() const;
//访问容器相关函数
T& front();
T& back();
const T& front() const;
const T& back() const;
//插入、删除函数
void insert(iterator pos, const T& x);
iterator erase(iterator pos);
void push_back(const T& x);
void pop_back();
void push_front(const T& x);
void pop_front();
//其他函数
size_t size() const;
void resize(size_t n, const T& val = T());
void clear();
bool empty() const;
void swap(list<T>& lt);
private:
node* _head; //指向链表头结点的指针
};
}
4.2迭代器类
因为string和vector对象都将其数据存储在了一块连续的内存空间,我们通过指针进行自增、自减以及解引用等操作,就可以对相应位置的数据进行一系列操作,因此string和vector当中的迭代器就是原生指针。但是对于list来说,其各个结点在内存当中的位置是随机的,并不是连续的,我们不能仅通过结点指针的自增、自减以及解引用等操作对相应结点的数据进行操作。而迭代器的意义就是,让使用者可以不必关心容器的底层实现,可以用简单统一的方式对容器内的数据进行访问。既然list的结点指针的行为不满足迭代器定义,那么我们可以对这个结点指针进行封装,对结点指针的各种运算符操作进行重载,使得我们可以用和string和vector当中的迭代器一样的方式使用list当中的迭代器。例如,当你使用list当中的迭代器进行自增操作时,实际上执行了p = p->next语句。list迭代器类,实际上就是对结点指针进行了封装,对其各种运算符进行了重载,使得结点指针的各种行为看起来和普通指针一样。(例如,对结点指针自增就能指向下一个结点)
5.六大组件-容器-序列式容器-C++98 deque
6.六大组件-容器-序列式容器-C++11 array
7.六大组件-容器-序列式容器-C++11 forward_list
8.六大组件-容器-关联式容器-map/set/multimap/multiset
8.1区别:map和set区别
1.Map是键值对,Set是值的集合,当然键和值可以是任何的值;
2.Map可以通过get方法获取值,而set不能因为它只有值;
3.都能通过迭代器进行for...of遍历;
4.Set的值是唯一的可以做数组去重,Map由于没有格式限制,可以做数据存储
5.map和set都是stl中的关联容器,map以键值对的形式存储,key=value组成pair,是一组映射关系。set只有值,可以认为只有一个数据,并且set中元素不可以重复且自动排序。
9.六大组件-容器-关联式容器-二叉树搜索树
9.1 概念特性
二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。
- 若它的右子树不为空,则右子树上所有结点的值都大于根结点的值。
- 它的左右子树也分别是二叉搜索树。
9.2 性能分析
最优的情况下,二叉搜索树为完全二叉树,其平均比较次数为:l o g N
最差的情况下,二叉搜索树退化为单支树,其平均比较次数为:N / 2
而时间复杂度描述的是最坏情况下算法的效率,因此普通二叉搜索树各个操作的时间复杂度都是O ( N )
9.3 删除的模拟实现
//递归删除函数的子函数(方法二)
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr) //空树
return false; //删除失败,返回false
if (key < root->_key) //key值小于根结点的值
return _EraseR(root->_left, key); //待删除结点在根的左子树当中
else if (key > root->_key) //key值大于根结点的值
return _EraseR(root->_right, key); //待删除结点在根的右子树当中
else //找到了待删除结点
{
if (root->_left == nullptr) //待删除结点的左子树为空
{
Node* del = root; //保存根结点
root = root->_right; //根的右子树作为二叉树新的根结点
delete del; //释放根结点
}
else if (root->_right == nullptr) //待删除结点的右子树为空
{
Node* del = root; //保存根结点
root = root->_left; //根的左子树作为二叉树新的根结点
delete del; //释放根结点
}
else //待删除结点的左右子树均不为空
{
Node* minRight = root->_right; //标记根结点右子树当中值最小的结点
//寻找根结点右子树当中值最小的结点
while (minRight->_left)
{
//一直往左走
minRight = minRight->_left;
}
K minKey = minRight->_key; //记录minRight结点的值
_EraseR(root->_right, minKey); //删除右子树当中值为minkey的结点,即删除minRight
root->_key = minKey; //将根结点的值改为minRight的值
}
return true; //删除成功,返回true
}
}
//递归删除函数(方法二)
bool EraseR(const K& key)
{
return _EraseR(_root, key); //删除_root当中值为key的结点
}
10.六大组件-容器-关联式容器-AVL树
10.1 概念:
二叉树搜索树 + 平因子的限制
10.2 特性
树的左右子树都是AVL树。
树的左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/01)。
10.3 查找效率
AVL树是一棵绝对平衡的二叉搜索树,其要求每个结点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即l o g N logNlogN。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
因此,如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但当一个结构经常需要被修改时,AVL树就不太适合了。
10.4 插入的实现
//插入函数
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr) //若AVL树为空树,则插入结点直接作为根结点
{
_root = new Node(kv);
return true;
}
//1、按照二叉搜索树的插入方法,找到待插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first < cur->_kv.first) //待插入结点的key值小于当前结点的key值
{
//往该结点的左子树走
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first) //待插入结点的key值大于当前结点的key值
{
//往该结点的右子树走
parent = cur;
cur = cur->_right;
}
else //待插入结点的key值等于当前结点的key值
{
//插入失败(不允许key值冗余)
return false;
}
}
//2、将待插入结点插入到树中
cur = new Node(kv); //根据所给值构造一个新结点
if (kv.first < parent->_kv.first) //新结点的key值小于parent的key值
{
//插入到parent的左边
parent->_left = cur;
cur->_parent = parent;
}
else //新结点的key值大于parent的key值
{
//插入到parent的右边
parent->_right = cur;
cur->_parent = parent;
}
//3、更新平衡因子,如果出现不平衡,则需要进行旋转
while (cur != _root) //最坏一路更新到根结点
{
if (cur == parent->_left) //parent的左子树增高
{
parent->_bf--; //parent的平衡因子--
}
else if (cur == parent->_right) //parent的右子树增高
{
parent->_bf++; //parent的平衡因子++
}
//判断是否更新结束或需要进行旋转
if (parent->_bf == 0) //更新结束(新增结点把parent左右子树矮的那一边增高了,此时左右高度一致)
{
break; //parent树的高度没有发生变化,不会影响其父结点及以上结点的平衡因子
}
else if (parent->_bf == -1 || parent->_bf == 1) //需要继续往上更新平衡因子
{
//parent树的高度变化,会影响其父结点的平衡因子,需要继续往上更新平衡因子
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2) //需要进行旋转(此时parent树已经不平衡了)
{
if (parent->_bf == -2)
{
if (cur->_bf == -1)
{
RotateR(parent); //右单旋
}
else //cur->_bf == 1
{
RotateLR(parent); //左右双旋
}
}
else //parent->_bf == 2
{
if (cur->_bf == -1)
{
RotateRL(parent); //右左双旋
}
else //cur->_bf == 1
{
RotateL(parent); //左单旋
}
}
break; //旋转后就一定平衡了,无需继续往上更新平衡因子(旋转后树高度变为插入之前了)
}
else
{
assert(false); //在插入前树的平衡因子就有问题
}
}
return true; //插入成功
}
11.六大组件-容器-关联式容器-红黑树
11.1概念:
概念:二叉搜索树 + 节点的颜色限制 + 性质的约束--->保证:最长路径中节点个数一定不会超过最短路径中节点个数的2倍---红黑树是一棵近似平衡的二叉树
11.2查找效率:
查找效率:不输AVL树--->O(logN)
11.3性质:
- 每个结点不是红色就是黑色。
- 根结点是黑色的。
- 如果一个结点是红色的,则它的两个孩子结点是黑色的。
- 对于每个结点,从该结点到其所有后代叶子结点的简单路径上,均包含相同数目的黑色结点。
- 每个叶子结点都是黑色的(此处的叶子结点指定是空结点)。
11.4插入的实现:
- 按二叉搜索树的插入方法,找到待插入位置。
- 将待插入结点插入到树中。
- 若插入结点的父结点是红色的,则需要对红黑树进行调整。
//插入函数
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr) //若红黑树为空树,则插入结点直接作为根结点
{
_root = new Node(kv);
_root->_col = BLACK; //根结点必须是黑色
return make_pair(_root, true); //插入成功
}
//1、按二叉搜索树的插入方法,找到待插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kv.first < cur->_kv.first) //待插入结点的key值小于当前结点的key值
{
//往该结点的左子树走
parent = cur;
cur = cur->_left;
}
else if (kv.first > cur->_kv.first) //待插入结点的key值大于当前结点的key值
{
//往该结点的右子树走
parent = cur;
cur = cur->_right;
}
else //待插入结点的key值等于当前结点的key值
{
return make_pair(cur, false); //插入失败
}
}
//2、将待插入结点插入到树中
cur = new Node(kv); //根据所给值构造一个结点
Node* newnode = cur; //记录新插入的结点(便于后序返回)
if (kv.first < parent->_kv.first) //新结点的key值小于parent的key值
{
//插入到parent的左边
parent->_left = cur;
cur->_parent = parent;
}
else //新结点的key值大于parent的key值
{
//插入到parent的右边
parent->_right = cur;
cur->_parent = parent;
}
//3、若插入结点的父结点是红色的,则需要对红黑树进行调整
while (parent&&parent->_col == RED)
{
Node* grandfather = parent->_parent; //parent是红色,则其父结点一定存在
if (parent == grandfather->_left) //parent是grandfather的左孩子
{
Node* uncle = grandfather->_right; //uncle是grandfather的右孩子
if (uncle&&uncle->_col == RED) //情况1:uncle存在且为红
{
//颜色调整
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else //情况2+情况3:uncle不存在 + uncle存在且为黑
{
if (cur == parent->_left)
{
RotateR(grandfather); //右单旋
//颜色调整
grandfather->_col = RED;
parent->_col = BLACK;
}
else //cur == parent->_right
{
RotateLR(grandfather); //左右双旋
//颜色调整
grandfather->_col = RED;
cur->_col = BLACK;
}
break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理
}
}
else //parent是grandfather的右孩子
{
Node* uncle = grandfather->_left; //uncle是grandfather的左孩子
if (uncle&&uncle->_col == RED) //情况1:uncle存在且为红
{
//颜色调整
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
//继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else //情况2+情况3:uncle不存在 + uncle存在且为黑
{
if (cur == parent->_left)
{
RotateRL(grandfather); //右左双旋
//颜色调整
cur->_col = BLACK;
grandfather->_col = RED;
}
else //cur == parent->_right
{
RotateL(grandfather); //左单旋
//颜色调整
grandfather->_col = RED;
parent->_col = BLACK;
}
break; //子树旋转后,该子树的根变成了黑色,无需继续往上进行处理
}
}
}
_root->_col = BLACK; //根结点的颜色为黑色(可能被情况一变成了红色,需要变回黑色)
return make_pair(newnode, true); //插入成功
}
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
//建立subRL与parent之间的联系
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
//建立parent与subR之间的联系
subR->_left = parent;
parent->_parent = subR;
//建立subR与parentParent之间的联系
if (parentParent == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;
//建立subLR与parent之间的联系
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
//建立parent与subL之间的联系
subL->_right = parent;
parent->_parent = subL;
//建立subL与parentParent之间的联系
if (parentParent == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
//左右双旋
void RotateLR(Node* parent)
{
RotateL(parent->_left);
RotateR(parent);
}
//右左双旋
void RotateRL(Node* parent)
{
RotateR(parent->_right);
RotateL(parent);
}
11.5正向迭代器:
红黑树的正向迭代器实际上就是对结点指针进行了封装,因此在正向迭代器当中实际上就只有一个成员变量,那就是正向迭代器所封装结点的指
//正向迭代器
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
typedef Ref reference; //结点指针的引用
typedef Ptr pointer; //结点指针
typedef RBTreeNode<T> Node; //结点的类型
typedef __TreeIterator<T, Ref, Ptr> Self; //正向迭代器的类型
Node* _node; //正向迭代器所封装结点的指针
//构造函数
__TreeIterator(Node* node)
:_node(node) //根据所给结点指针构造一个正向迭代器
{}
Ref operator*()
{
return _node->_data; //返回结点数据的引用
}
Ptr operator->()
{
return &_node->_data; //返回结点数据的指针
}
//判断两个正向迭代器是否不同
bool operator!=(const Self& s) const
{
return _node != s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//判断两个正向迭代器是否相同
bool operator==(const Self& s) const
{
return _node == s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//前置++
Self operator++()
{
if (_node->_right) //结点的右子树不为空
{
//寻找该结点右子树当中的最左结点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left; //++后变为该结点
}
else //结点的右子树为空
{
//寻找孩子不在父亲右的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //++后变为该结点
}
return *this;
}
//前置--
Self operator--()
{
if (_node->_left) //结点的左子树不为空
{
//寻找该结点左子树当中的最右结点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right; //--后变为该结点
}
else //结点的左子树为空
{
//寻找孩子不在父亲左的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //--后变为该结点
}
return *this;
}
};
11.6反向迭代器:
红黑树的反向迭代器实际上就是正向迭代器的一个封装,因此红黑树的反向迭代器就是一个迭代器适配器。
//反向迭代器---迭代器适配器
template<class Iterator>
struct ReverseIterator
{
typedef ReverseIterator<Iterator> Self; //反向迭代器的类型
typedef typename Iterator::reference Ref; //结点指针的引用
typedef typename Iterator::pointer Ptr; //结点指针
Iterator _it; //反向迭代器所封装的正向迭代器
//构造函数
ReverseIterator(Iterator it)
:_it(it) //根据所给正向迭代器构造一个反向迭代器
{}
Ref operator*()
{
return *_it; //通过调用正向迭代器的operator*返回结点数据的引用
}
Ptr operator->()
{
return _it.operator->(); //通过调用正向迭代器的operator->返回结点数据的指针
}
//前置++
Self& operator++()
{
--_it; //调用正向迭代器的前置--
return *this;
}
//前置--
Self& operator--()
{
++_it; //调用正向迭代器的前置++
return *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it; //调用正向迭代器的operator!=
}
bool operator==(const Self& s) const
{
return _it == s._it; //调用正向迭代器的operator==
}
};
11.7set的模拟实现:
template<class K>
class set
{
//仿函数
struct SetKeyOfT
{
const K& operator()(const K& key) //返回键值Key
{
return key;
}
};
public:
typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator; //正向迭代器
typedef typename RBTree<K, K, SetKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
//插入函数
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, K, SetKeyOfT> _t;
};
11.8map的模拟实现:
template<class K, class V>
class map
{
//仿函数
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv) //返回键值对当中的键值Key
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator; //正向迭代器
typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::reverse_iterator reverse_iterator; //反向迭代器
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
reverse_iterator rbegin()
{
return _t.rbegin();
}
reverse_iterator rend()
{
return _t.rend();
}
//插入函数
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
//[]运算符重载函数
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
iterator it = ret.first;
return it->second;
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
private:
RBTree<K, pair<K, V>, MapKeyOfT> _t;
};
12.六大组件-容器-底层为哈希结构-unordered_map/set/multimap/multiset
map:
优点:有序性,内部实现的红黑树的查找,插入和删除的复杂度都是O(logn),因此效率非常高。
缺点:空间占用率高,因为map内部实现了红黑树,虽然提高了运行效率,但是因为每一个节点都需要额外保存父节点,孩子节点和红。黑性质,使得每一个节点都占用大量的空间。
适用:对于有顺序要求的问题,用map会高效一些。
unordered_map:
优点:因为内部实现哈希表,因此其查找速度非常快
缺点:哈希表的建立比较耗费时间,有可能还会哈希冲突(开链法避免地址冲突)
适用:常用于查找问题。
13.六大组件-容器-底层为哈希结构-哈希
13.1哈希概念:
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。搜索的效率取决于搜索过程中元素的比较次数,因此顺序结构中查找的时间复杂度为O(N),平衡树中查找的时间复杂度为树的高度O(logN)。
而最理想的搜索方法是,可以不经过任何比较,一次直接从表中得到要搜索的元素,即查找的时间复杂度为O(1)。
如果构造一种存储结构,该结构能够通过某种函数使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时就能通过该函数很快找到该元素。
向该结构当中插入和搜索元素的过程如下:
插入元素: 根据待插入元素的关键码,用此函数计算出该元素的存储位置,并将元素存放到此位置。
搜索元素: 对元素的关键码进行同样的计算,把求得的函数值当作元素的存储位置,在结构中按此位置取元素进行比较,若关键码相等,则搜索成功。
该方式即为哈希(散列)方法, 哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(散列表)。
13.2哈希冲突:
不同关键字通过相同哈希函数计算出相同的哈希地址,这种现象称为哈希冲突或哈希碰撞。我们把关键码不同而具有相同哈希地址的数据元素称为“同义词”。
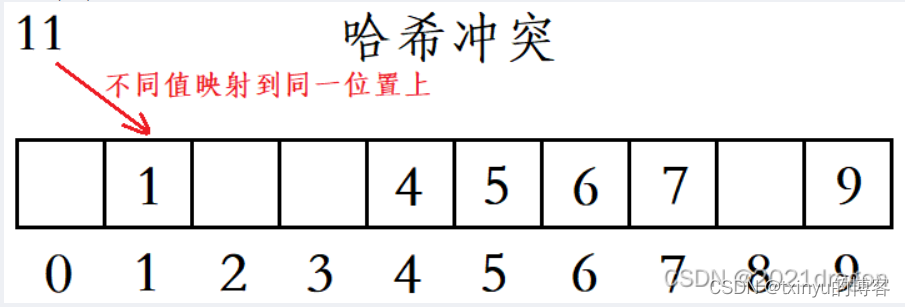
解决哈希冲突有两种常见的方法:闭散列和开散列。
13.3位图
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
常见位图的应用如下:
- 快速查找某个数据是否在一个集合中。
- 排序。
- 求两个集合的交集、并集等。
- 操作系统中磁盘块标记。
- 内核中信号标志位(信号屏蔽字和未决信号集)。
接口一览:
namespace cl
{
//模拟实现位图
template<size_t N>
class bitset
{
public:
//构造函数
bitset();
//设置位
void set(size_t pos);
//清空位
void reset(size_t pos);
//反转位
void flip(size_t pos);
//获取位的状态
bool test(size_t pos);
//获取可以容纳的位的个数
size_t size();
//获取被设置位的个数
size_t count();
//判断位图中是否有位被设置
bool any();
//判断位图中是否全部位都没有被设置
bool none();
//判断位图中是否全部位都被设置
bool all();
//打印函数
void Print();
private:
vector<int> _bits; //位图
};
}
13.4布隆过滤器
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询。
布隆过滤器其实就是位图的一个变形和延申,虽然无法避免存在哈希冲突,但我们可以想办法降低误判的概率。
当一个数据映射到位图中时,布隆过滤器会用多个哈希函数将其映射到多个比特位,当判断一个数据是否在位图当中时,需要分别根据这些哈希函数计算出对应的比特位,如果这些比特位都被设置为1则判定为该数据存在,否则则判定为该数据不存在。
布隆过滤器使用多个哈希函数进行映射,目的就在于降低哈希冲突的概率,一个哈希函数产生冲突的概率可能比较大,但多个哈希函数同时产生冲突的概率可就没那么大了。
特点:
- 当布隆过滤器判断一个数据存在可能是不准确的,因为这个数据对应的比特位可能被其他一个数据或多个数据占用了。
- 当布隆过滤器判断一个数据不存在是准确的,因为如果该数据存在那么该数据对应的比特位都应该已经被设置为1了。
优点:
增加和查询元素的时间复杂度为O(K)(K为哈希函数的个数,一般比较小),与数据量大小无关。
哈希函数相互之间没有关系,方便硬件并行运算。
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势。
在能够承受一定的误判时,布隆过滤器比其他数据结构有着很大的空间优势。
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能。
使用同一组哈希函数的布隆过滤器可以进行交、并、差运算。
使用场景:
比如当我们首次访问某个网站时需要用手机号注册账号,而用户的各种数据实际都是存储在数据库当中的,也就是磁盘上面。
当我们用手机号注册账号时,系统就需要判断你填入的手机号是否已经注册过,如果注册过则会提示用户注册失败。
但这种情况下系统不可能直接去遍历磁盘当中的用户数据,判断该手机号是否被注册过,因为磁盘IO是很慢的,这会降低用户的体验。
这种情况下就可以使用布隆过滤器,将所有注册过的手机号全部添加到布隆过滤器当中,当我们需要用手机号注册账号时,就可以直接去布隆过滤器当中进行查找。
如果在布隆过滤器中查找后发现该手机号不存在,则说明该手机号没有被注册过,此时就可以让用户进行注册,并且避免了磁盘IO。
如果在布隆过滤器中查找后发现该手机号存在,此时还需要进一步访问磁盘进行复核,确认该手机号是否真的被注册过,因为布隆过滤器在判断元素存在时可能会误判。
14.六大组件-迭代器
一种设计模式
概念:行为像指一样的类型,可能是指针可能是被类封装的指针,不关注容器底层细节的情况下可以轻松访问容器
如何给你一个容器增加迭代器:
实现迭代器类:构造函数、具有指针类似的行为(operator*(),operator->())、要能够移动(++的重载,--的重载:有些容器不需要实现-- 比如:单链表)、迭代器要能比较(==,!=)、
在容器类中迭代器类取别名 typedef ... iterator、增加begin和end方法
迭代器失效:
1.迭代器指向的空间野指针。2.迭代器指向的位置已经不是原来的位置,意义变了。
vector insert扩容导致野指针,insert不扩容但是挪动数据,指向的位置已经不是原来的位置,erase之后挪动位置但是指向的位置已经不是原来的位置,list删除结点之后导致野指针,map/set删除结点之后导致野指针
避免迭代器失效的方法:
1. 通过使用一些操作,如swap()、emplace()、push_back()、pop_back()等,可以避免迭代器失效。
2. 在遍历容器时,将元素的值赋值给变量,而不是访问迭代器本身。
3. 利用erase()、insert()、clear()等函数返回值更新相关的迭代器或者使用基于下标的操作访问容器。
15.六大组件-算反
16.六大组件-适配器
容器适配器 迭代适配器
17.六大组件-仿函数
实现方式:在类中将函数调用运算符()重载
作用:让代码更加灵活