目录
前言:
一、B树
1、B树概念
2、B树查找
3、B树插入
4、B树前序遍历
5、B树性能
二、B+、B*树
1、B+树概念
2、B+树的插入
2、B*树概念
3、总结
三、B系列树的应用
总结
前言:
我们已经有很多索引的数据结构了
例如:
一、B树
1、B树概念
1970年,R.Bayer和E.mccreight提出了一种适用于外查找的树,它是一种平衡的多叉树,称为B树(或B-树、B_树)。
一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
最多有9个关键字,10个孩子
向上取整的原因会在插入时说明
同时每一层的关键字按特定的顺序排列(升序,降序,可以使用仿函数来控制)

2、B树查找
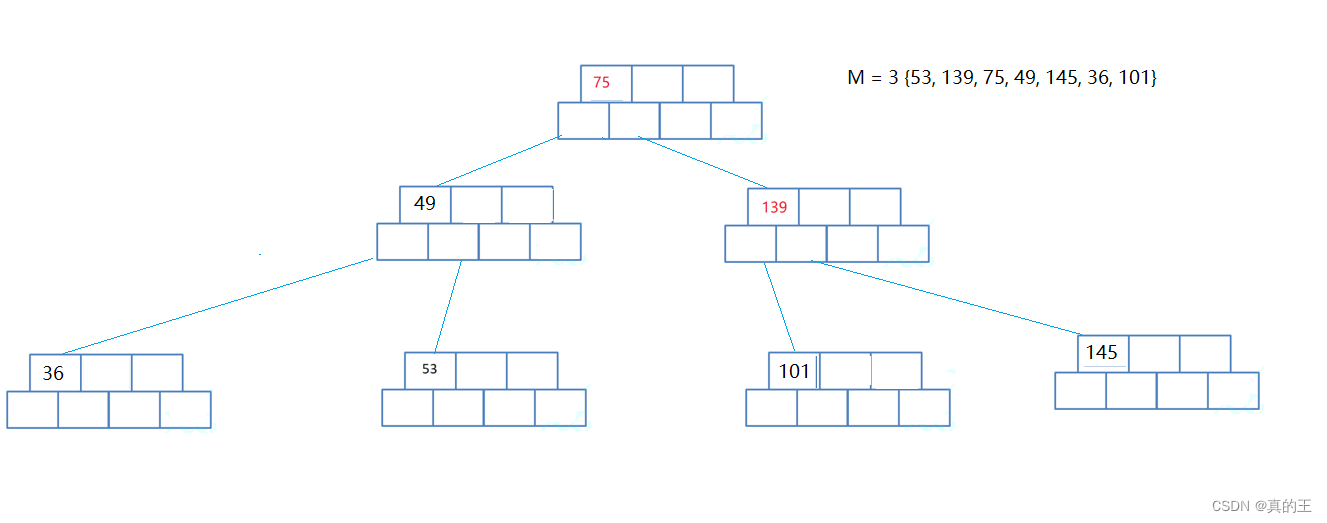
还是以上图为例,现在要找53
寻找的思路与二叉搜索树类型,不过这次是在一个数组中寻找,
它既要在纵向上搜索,也要在横向上搜索
先在横向搜索,从左向右遍历找到与它的key相等的节点,如果不相等比它小,就继续向右遍历
比它小就到下一层寻找,直到找到该节点或者将整棵树遍历完都没有找到
为了提高效率,因为对于每一个节点来说,它是有序的,可以使用二分查找提高查找效率
同时为了方便实现Insert,我们将Find的返回值类型定义为pair<Node*, int>
如果能够找到就返回该节点的地址,及它在该节点位置的下标
找不到就返回它的父节点及-1,可以根据pair的second来判断是否找到该节点
找到它的父节点就可以方便进行插入了
// 顺序遍历
std::pair<Node *, int> Find(const K &key)
{
Node *cur = _root;
Node *parent = nullptr;
while (cur)
{
size_t i = 0;
while (i < cur->_n)
{
if (key < cur->_keys[i])
{
break;
}
else if (key > cur->_keys[i])
{
i++;
}
else
{
return std::make_pair(cur, i);
}
}
parent = cur;
cur = cur->_subs[i];
}
return std::make_pair(parent, -1);
}
// 二分查找
std::pair<Node *, int> Find(const K &key)
{
Node *cur = _root;
Node *parent = nullptr;
while (cur)
{
int left = 0;
int right = cur->_n - 1;
while (left <= right)
{
int mid = (left + right) >> 1;
if (key < cur->_keys[mid])
{
right = mid - 1;
}
else if (key > cur->_keys[mid])
{
left = mid + 1;
}
else
{
return std::make_pair(cur, mid);
}
}
parent = cur;
cur = cur->_subs[left];
}
return std::make_pair(parent, -1);
}3、B树插入
B树的插入,如果不考虑分裂是比较简单的
bool Insert(const K &key, const V &val)
{
if (_root == nullptr)
{
_root = new Node;
_root->_keys[0] = key;
_root->_val[0] = val;
_root->_n++;
return true;
}
return true;
}接下来看具体的插入过程

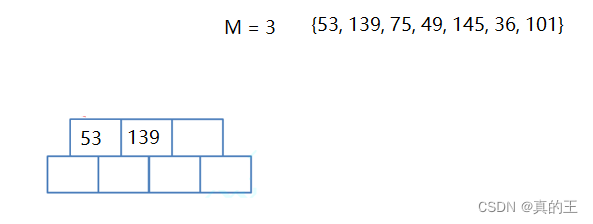

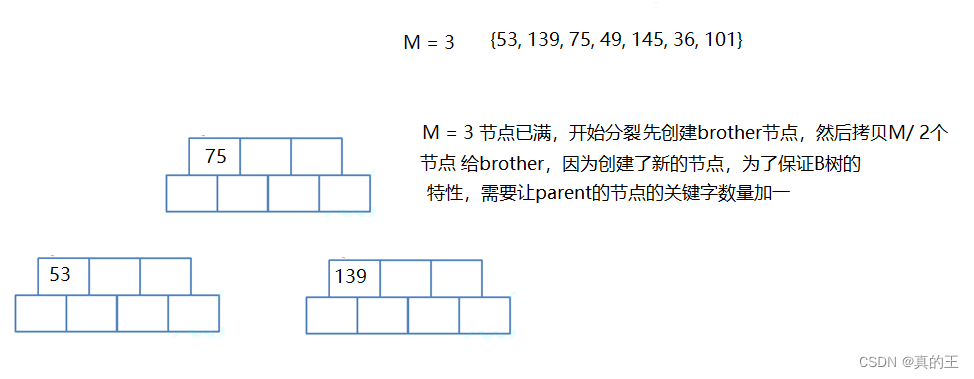
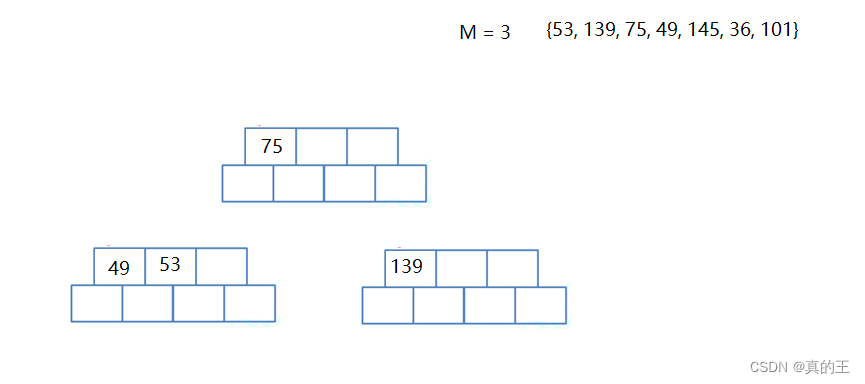

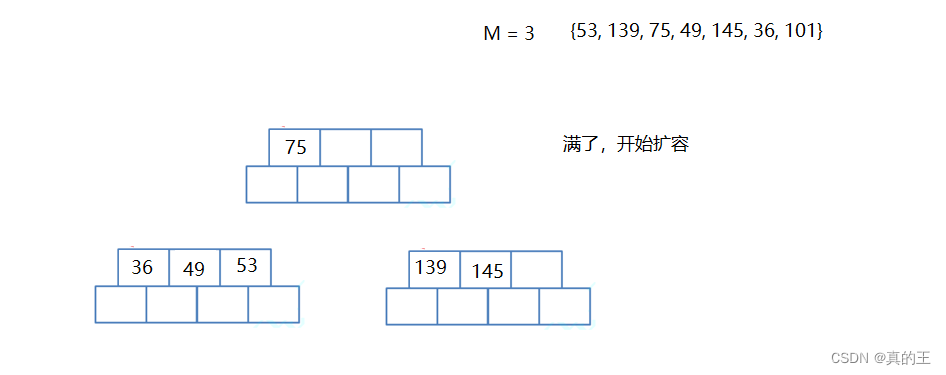


void InsertKey(Node *node, const K &key, const V &val, Node *child)
{
int end = node->_n - 1;
while (end >= 0)
{
if (key < node->_keys[end])
{
node->_keys[end + 1] = node->_keys[end];
node->_val[end + 1] = node->_val[end];
// child 也要对应上
node->_subs[end + 2] = node->_subs[end + 1];
end--;
}
else
{
break;
}
}
// 先插入key
node->_keys[end + 1] = key;
node->_val[end + 1] = val;
// 最后插入child,关键字比节点数少一
node->_subs[end + 2] = child;
if (child)
{
child->_parent = node;
}
node->_n++;
}
bool Insert(const K &key, const V &val)
{
if (_root == nullptr)
{
_root = new Node;
_root->_keys[0] = key;
_root->_val[0] = val;
_root->_n++;
return true;
}
// 插入节点过程
K newKey = key;
V newVal = val;
Node *child = nullptr;
std::pair<Node *, int> ret = Find(newKey);
//说明已经存在该节点了,不用插入
if (ret.second >= 0)
{
return false;
}
Node *parent = ret.first;
while (true)
{
InsertKey(parent, newKey, newVal, child);
if (parent->_n < M)
{
return true;
}
// B树满了,开始分裂,创建新节点,并且将原节点的一半拷贝给brother
size_t mid = M / 2;
Node *brother = new Node;
size_t j = 0;
size_t i = mid + 1;
for (; i < M; i++)
{
brother->_keys[j] = parent->_keys[i];
brother->_val[j] = parent->_keys[i];
brother->_subs[j] = parent->_subs[i];
// parent->child->parent = brother
if (parent->_subs[i])
{
parent->_subs[i]->_parent = brother;
}
// 处理干净,指针必须处理,val可以不处理
parent->_keys[i] = K();
parent->_val[i] = V();
parent->_subs[i] = nullptr;
j++;
}
// child比key多一个,处理最后的右子树
brother->_subs[j] = parent->_subs[i];
if (parent->_subs[i])
{
parent->_subs[i]->_parent = brother;
}
parent->_subs[i] = nullptr;
brother->_n = j;
parent->_n -= j + 1; // 还有一个节点给了parent
K midKey = parent->_keys[mid];
K midVal = parent->_val[mid];
parent->_keys[mid] = K();
parent->_val[mid] = V();
//说明刚才分裂的是根节点
if (parent->_parent == nullptr)
{
_root = new Node;
_root->_keys[0] = midKey;
_root->_val[0] = midVal;
_root->_subs[0] = parent;
_root->_subs[1] = brother;
_root->_n = 1;
parent->_parent = _root;
brother->_parent = _root;
break;
}
else
{
// 转化为parent->parent 中插入 newKey和brother
newKey = midKey;
newVal = midVal;
child = brother;
parent = parent->_parent;
}
}
return true;
}4、B树前序遍历
它的前序遍历就是多叉树的前序遍历,同时不要忘记最后的右子树
void _InOrder(Node *root)
{
if (root == nullptr)
{
return;
}
//左树,根,左树,根,左树,根……
size_t i = 0;
for (; i < root->_n; i++)
{
_InOrder(root->_subs[i]);
std::cout << "Key " << root->_keys[i] << " : "
<< "val " << root->_val[i] << std::endl;
}
//右数
_InOrder(root->_subs[i]);
}
void InOrder()
{
_InOrder(_root);
}5、B树性能
二、B+、B*树
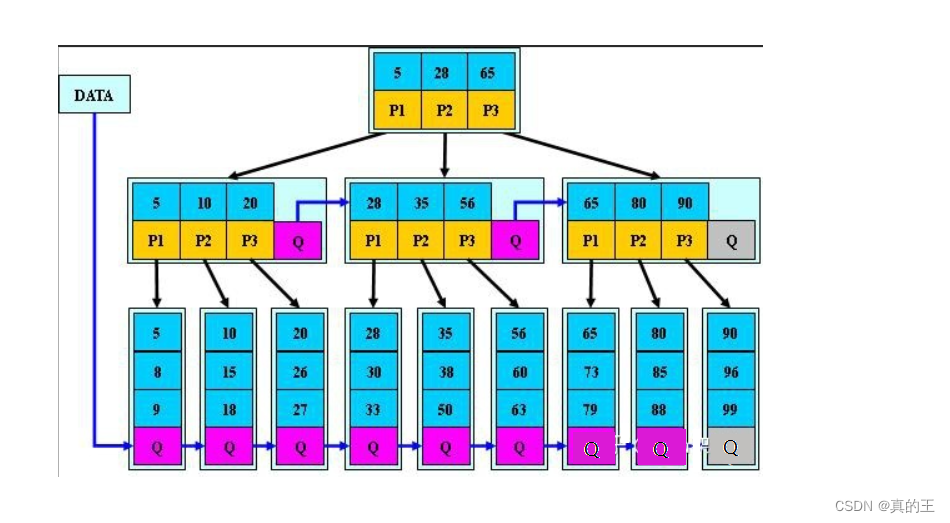
1、B+树概念

总结:
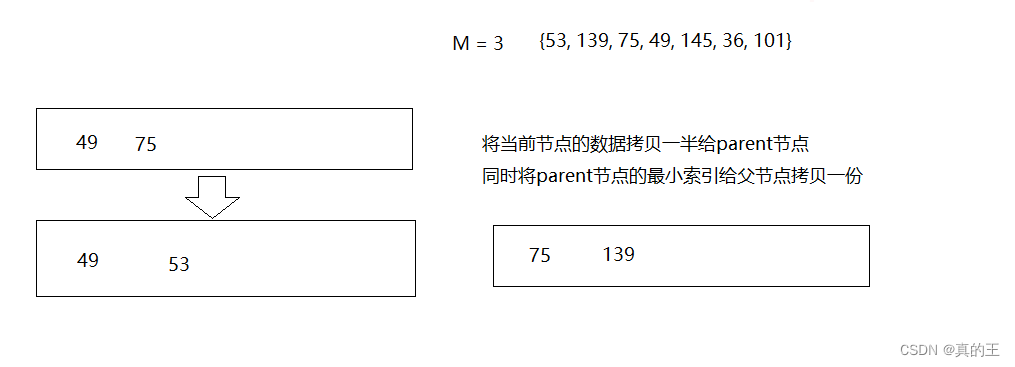
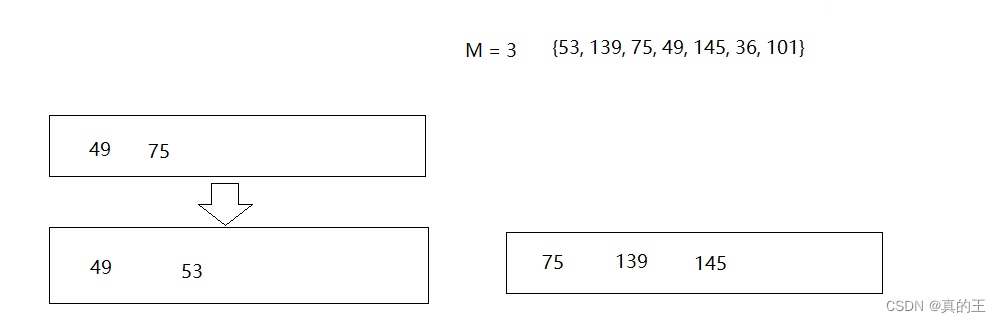
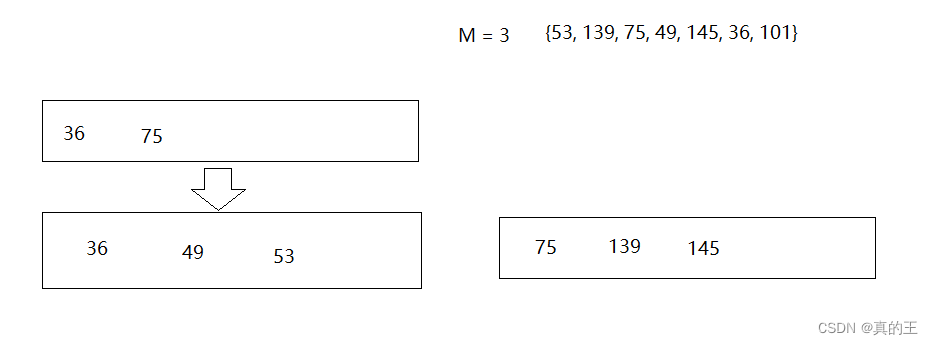
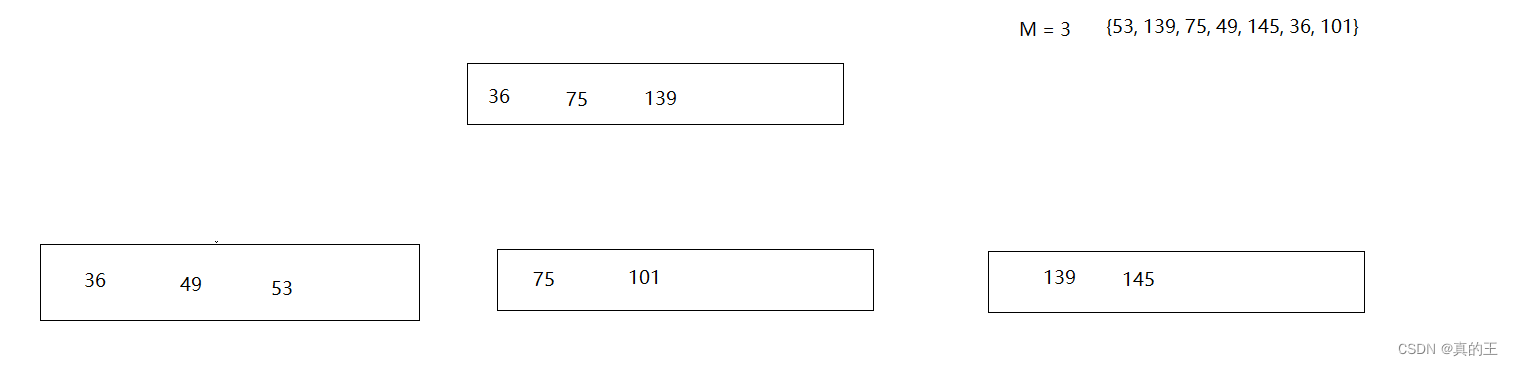
分支节点跟叶子节点有重复的值,分支节点存的是叶子结点的索引
父亲中存的是孩子节点中的最小值做索引
B+树特性:
所有关键字都出现在叶子节点的链表中,且链表中的节点都是有序的
在分支节点无法获取value
分支节点相当于是叶子节点的索引,叶子节点才是存储数据的
2、B+树的插入
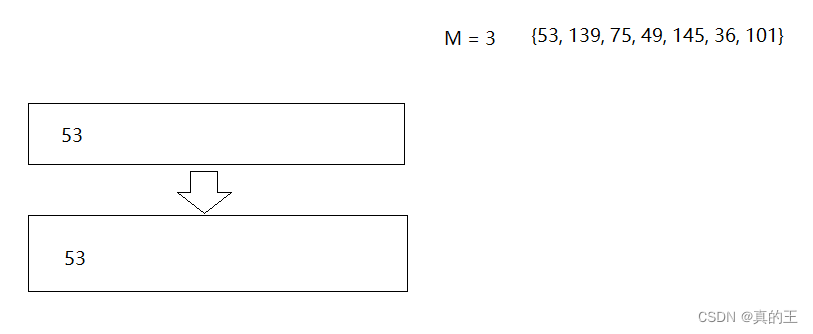
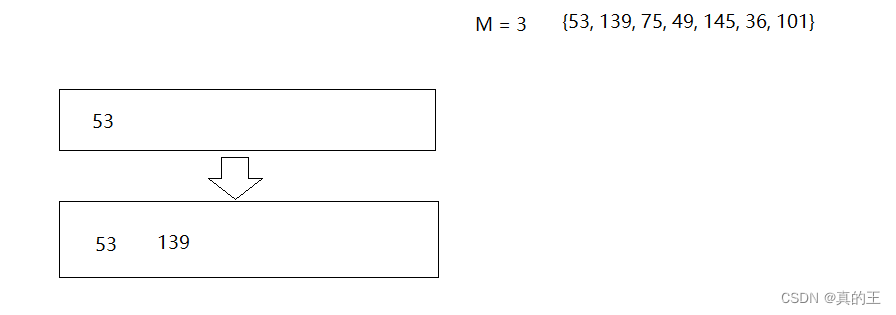

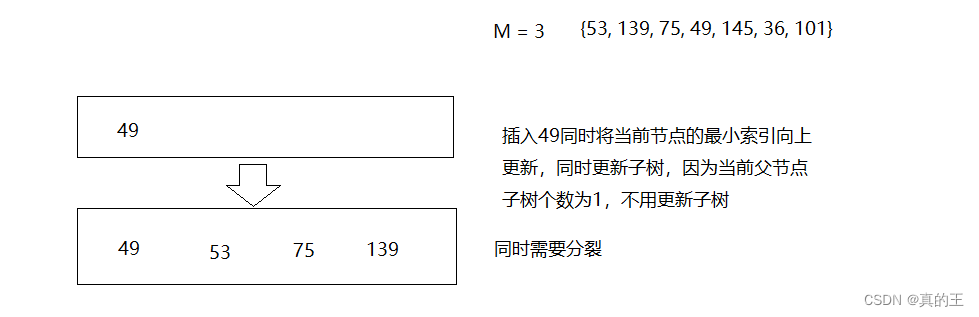
2、B*树概念
3、总结
三、B系列树的应用
总结
以上就是今天要讲的内容,本文仅仅简单介绍了B树的相关概念






![[毕业设计]2022-2023年最新最全计算机专业毕设选题推荐汇总](https://img-blog.csdnimg.cn/887a898b20664b399694dcf15cedcd68.png)