给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

提示:

• 1 <= nums.length <= 10^4
• -10^9 <= nums[i] <= 10^9

思路

本题属于循环数组问题，循环数组的处理，我们可以将两个nums数组拼接在一起，使用单调栈计算出每一个元素的下一个最大值，最后再把结果集即result数组resize到原数组大小即可。

但这种写法，修改了nums数组，而且最后还要把result数组resize回去。resize倒是不费时间，是O(1)的操作，但扩充nums数组相当于**多了一个O(n)**的操作。时间复杂度和空间复杂度都多了O(n)。

写法1完整版

// 版本一
class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        // 拼接一个新的nums
        vector<int> nums1(nums.begin(), nums.end());
        nums.insert(nums.end(), nums1.begin(), nums1.end());
        // 用新的nums大小来初始化result
        vector<int> result(nums.size(), -1);
        if (nums.size() == 0) return result;

        // 开始单调栈
        stack<int> st;
        st.push(0);
        for (int i = 1; i < nums.size(); i++) { 
            if (nums[i] < nums[st.top()]) st.push(i); 
            else if (nums[i] == nums[st.top()]) st.push(i);
            else { 
                while (!st.empty() && nums[i] > nums[st.top()]) {
                    result[st.top()] = nums[i];
                    st.pop();
                }
                st.push(i);
            }
        }
        // 最后再把结果集即result数组resize到原数组大小
        result.resize(nums.size() / 2);
        return result;
    }
};

环形数组处理：i取模，遍历两遍

对于这种循环数组， nums[nums.length - 1] 的下一个元素是 nums[0] ，需要遍历两遍，可以通过给i取模来解决！

我们首先扩充for循环遍历范围，令for遍历范围为[0,nums.size()*2-1]（这样就遍历了2n个位置，遍历长度为2n），然后nums[i]改为nums[i%nums.size()]。

由于取模运算的特性， i初始值=0，i%nums.size()这个式子就是0--nums.size()-1循环取值。

• 当i初始值=0时，i%a的范围就是[0,a-1]！

因为 “求模” 运算的定义是 “求余数”。例如，当 7 除以 3，结果是 2 余 1，所以 7%3 的结果是 1。余数总是会小于除数的，所以 i%a 的结果将始终在 0 到 a-1 的范围内。

当 i 小于 a 时，i%a 的结果就是 i 自己；当 i 等于 a 时，i%a 的结果就是 0；当 i 大于 a 时，i%a 的结果就是 i-a 的值，直到这个值小于 a 为止。

遍历两遍的逻辑：

st.push(0);
for(int i=1;i<nums.size()*2;i++){
    if(nums[i%nums.size()]<=nums[st.top()]){
        st.push(i%nums.size());
    }
    else{
        while(nums[i%nums.size()]>nums[st.top()]&&!st.empty()){
            result[st.top()]=nums[i%nums.size()];
            st.pop();
        }
        st.push(nums[i%nums.size()]);
    }
}

写法2完整版（环形数组推荐写法）

• 重点在只用O(n)的时间复杂度和空间复杂度，完成遍历两遍数组

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        stack<int>st;
        vector<int>result(nums.size(),-1);
        st.push(0);
        for(int i=1;i<nums.size()*2;i++){
            if(nums[i%nums.size()]<=nums[st.top()]){
                st.push(i%nums.size());
            }
            else{
                while(!st.empty()&&nums[i%nums.size()]>nums[st.top()]){
                    result[st.top()]=nums[i%nums.size()];
                    st.pop();
                }
                st.push(i%nums.size());
            }
        }
		return result;
    }
};

debug测试：

Line 171: Char 16: runtime error: reference binding to misaligned address 0xbebebebebebec0ba for type ‘int’, which requires 4 byte alignment (stl_deque.h) 0xbebebebebebec0ba: note: pointer points here

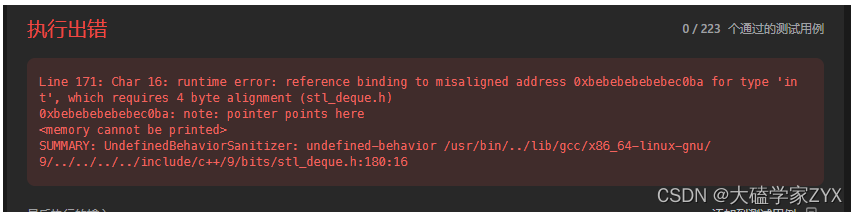
错误信息的意思是：运行时发生了一种未定义行为（Undefined Behavior）。具体来说，它在尝试对一个非对齐的地址（即不是4字节对齐的地址）进行整数的引用绑定，而这个操作是未定义的。该错误通常发生在空指针解引用，数组越界等情况。

这个错误出现在while循环这一句：

while(nums[i%nums.size()]>nums[st.top()]&&!st.empty())

while 循环如果这么写，那么，在检查栈是否为空之前，就已经尝试从栈顶取值，这是有问题的。当栈为空时，这将会导致未定义行为。

逻辑运算符短路特性

在C++中，逻辑AND操作符(&&)和逻辑OR操作符(||)都具有"短路"特性。

对于逻辑AND操作符，如果左边的操作数为假，那么不论右边的操作数是什么，整个表达式的结果都是假，因此不需要再计算右边的操作数。对于逻辑OR操作符，如果左边的操作数为真，那么不论右边的操作数是什么，整个表达式的结果都是真，因此不需要再计算右边的操作数。

因此，写单调栈的while循环，while条件里面包括了非空检查的时候，检查栈是否为空的语句必须放在前面，确定非空之后再尝试从栈顶取值！如果栈已经为空，那么!st.empty()的结果为假，右边的nums[i%nums.size()] > nums[st.top()]就不会被执行，从而避免对空栈进行操作的未定义行为。

result数组在栈口取元素，是否会覆盖原有数值？

答案是不会，因为result更新，是在发现了一个更大的数值，弹出的时候才会更新。

例如4 3 2这个例子，遍历两遍得到的是4 3 2 4 3 2，实际上后面那一组4 3 2的下标还是0 1 2，数组下标是没有扩展的。

但是遍历前面这一组4 3 2的时候，因为单调递减，所以全部入栈，栈内为2 3 4，遍历第二遍的时候遇到了4，栈内的2 3才被弹出，相当于result[1]和[2]此时更新。但是到了后面，3 2继续入栈，到最后2 3 4都留在了栈里面不会被弹出，因此也不可能导致result的值被覆盖！

再例如2 3 4的例子，遍历两遍得到2 3 4 2 3 4，第一遍的时候result就已经被填满，result[0]=3,result[1]=4,result[2]=-1。到了遍历第二遍的时候，此时栈内只有4，第二次遍历时，2入栈之后3再入栈，会弹出2，相当于result[0]仍然=3，同理result[1]仍然=4。即使是result的值覆盖了，结果依旧是不变的。