剑指 Offer 618 - II. 二叉树的最近公共祖先

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

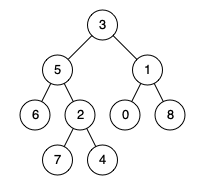
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

原题链接：https://leetcode.cn/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/

解题思路

这题官方给出的难度等级是简单，我个人认为这题在简单题里应该算是比较难的了 （可能是我比较菜🤣） 。

我的思路是用递归dfs的方式，找到每个节点及它下层的节点中满足条件的节点个数，在回溯的时候判断找到的节点个数是否等于2，就可以找出第一个公共父节点。

具体步骤：

1. 先保存要寻找的节点q和p，别弄丢了，由于这两个节点是后面每层递归都要用的，所以我选择用全局变量来保存，同时定义全局变量ans用来保存答案。
2. 定义递归的终止条件，当前节点为null的时候就需要终止了。
3. 定义count用于存储符合条件的节点个数，由于我们在递归的时候只判断当前这一层和下层节点的个数，故count在递归中定义为0即可。
4. 判断当前节点是否满足条件，题目中已经告诉我们每个节点的值都是不一样的了，所以我们直接用节点值判断即可，而且不需要担心重复值干扰count的情况。若满足就把count+1。
5. 递归左子树和右子树，获取他们当中满足条件的节点个数，并一起加到count当中。这样一来，count就等于当前节点和所有下层节点中满足条件的个数了。
6. 判断当前count值，是否等于2，等于2就说明已经找到q和p两个节点了，那当前节点肯定就是公共节点了。但这里要注意，我们只需要找到最近的那个公共祖先，由于递归是往上回溯的，所以第一个count==2的节点就是最近的公共祖先。为了防止上层节点重复赋值，所以我们同时要判断ans是否为null。
7. 递归结束后，答案已经被存到ans中了，我们直接返回ans即可。
8. 配合下面的AC代码来理解解题思路更佳噢~

Java AC代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 把值存起来，便于后面计算
        this.q = q;
        this.p = p;
        this.ans = null;
        dfs(root);
        return ans;
    }

    TreeNode q, p, ans;

    public int dfs(TreeNode now) {
        // 终止条件
        if (now == null) return 0;
        // count 用于记录本层和本层以下的所有满足条件的节点个数
        int count = 0;
        // 判断当前节点是否满足条件
        if ( now.val == p.val || now.val == q.val ) {
            count++;
        }
        // 判断下面几层的节点满足条件的个数
        count += dfs(now.left);
        count += dfs(now.right);
        // 如果满足条件的个数为2，且ans还没有被赋值
        // 说明这是第一个公共父节点，故把它存起来
        if (count == 2 && ans == null) {
            ans = now;
        }
        return count;
    }
}

运行速度还不错😋😋

题目分享

另外还有一道跟这题有点像的题目，也一起分享给大家：160. 相交链表 - 力扣（LeetCode）

这道相交链表其实也可以看成一个“二叉树”找最近的公共节点，只不过这个“二叉树”是尾巴节点指向头节点的，而我们正常二叉树是头节点指向子树节点的，所以这两道题其实解题思路是不同的，有兴趣的同学可以练习一下噢😋🤣。
实也可以看成一个“二叉树”找最近的公共节点，只不过这个“二叉树”是尾巴节点指向头节点的，而我们正常二叉树是头节点指向子树节点的，所以这两道题其实解题思路是不同的，有兴趣的同学可以练习一下噢😋🤣。