1 高斯函数的傅里叶变换
主要参考自
http://www.cse.yorku.ca/~kosta/CompVis_Notes/fourier_transform_Gaussian.pdf
对于中心化的高斯函数,即
g ( x ) = 1 2 π σ e − x 2 2 σ 2 , (1.1) g\left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{x^2}}}{{2{\sigma ^2}}}}},\tag{1.1} g(x)=2πσ1e−2σ2x2,(1.1)
对其求导可得
d g ( x ) d x = − x σ 2 g ( x ) . (1.2) \frac{{dg\left( x \right)}}{{dx}} = - \frac{x}{{{\sigma ^2}}}g\left( x \right).\tag{1.2} dxdg(x)=−σ2xg(x).(1.2)
根据傅里叶变换的性质,当对信号的导数进行傅里叶变换时,可得
∫ − ∞ ∞ d g ( x ) d x e − j ω x d x = ∫ − ∞ ∞ e − j ω x d g ( x ) = e − j ω x g ( x ) ∣ − ∞ ∞ − ∫ − ∞ ∞ g ( x ) d e − j ω x = j ω ∫ − ∞ ∞ g ( x ) e − j ω x d x = j ω G ( j ω ) . (1.3) \begin{array}{l} \int\limits_{ - \infty }^\infty {\frac{{dg\left( x \right)}}{{dx}}{e^{ - j\omega x}}dx} = \int\limits_{ - \infty }^\infty {{e^{ - j\omega x}}dg\left( x \right)} \\ = \left. {{e^{ - j\omega x}}g\left( x \right)} \right|_{ - \infty }^\infty - \int\limits_{ - \infty }^\infty {g\left( x \right)d{e^{ - j\omega x}}} \\ = j\omega \int\limits_{ - \infty }^\infty {g\left( x \right){e^{ - j\omega x}}dx} \\ = j\omega G\left( {j\omega } \right). \end{array} \tag{1.3} −∞∫∞dxdg(x)e−jωxdx=−∞∫∞e−jωxdg(x)=e−jωxg(x) −∞∞−−∞∫∞g(x)de−jωx=jω−∞∫∞g(x)e−jωxdx=jωG(jω).(1.3)
同理,当对信号的频谱的导数进行傅里叶反变换时,可得
1 2 π ∫ − ∞ ∞ d G ( j ω ) d ω e j ω x d ω = 1 2 π ∫ − ∞ ∞ e j ω x d G ( j ω ) = − j x 2 π ∫ − ∞ ∞ G ( j ω ) e j ω x d ω = − j x g ( x ) . (1.4) \begin{array}{l} \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {\frac{{dG\left( {j\omega } \right)}}{{d\omega }}{e^{j\omega x}}d\omega } = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty {{e^{j\omega x}}dG\left( {j\omega } \right)} \\ = - \frac{{jx}}{{2\pi }}\int\limits_{ - \infty }^\infty {G\left( {j\omega } \right){e^{j\omega x}}d\omega } \\ = - jxg\left( x \right). \end{array} \tag{1.4} 2π1−∞∫∞dωdG(jω)ejωxdω=2π1−∞∫∞ejωxdG(jω)=−2πjx−∞∫∞G(jω)ejωxdω=−jxg(x).(1.4)
于是分别对式 (1.2) 两侧进行傅里叶变换,可得
j ω G ( j ω ) = 1 j σ 2 d G ( j ω ) d ω ⇒ d G ( j ω ) d ω G ( j ω ) = − σ 2 ω . (1.5) j\omega G\left( {j\omega } \right) = \frac{1}{{j{\sigma ^2}}}\frac{{dG\left( {j\omega } \right)}}{{d\omega }} \Rightarrow {\textstyle{{\frac{{dG\left( {j\omega } \right)}}{{d\omega }}} \over {G\left( {j\omega } \right)}}} = - {\sigma ^2}\omega .\tag{1.5} jωG(jω)=jσ21dωdG(jω)⇒G(jω)dωdG(jω)=−σ2ω.(1.5)
因为 g ( x ) g\left( x \right) g(x) 属于实偶对称函数,所以其傅里叶变换同样为实偶对称函数,后面不妨忽略 G ( j ω ) G\left( {j\omega } \right) G(jω) 中的复数符号。对式 (1.5) 在 ( 0 , ω ) \left( {0,\omega } \right) (0,ω) 区间做积分,可得
∫ 0 ω d G ( υ ) d υ G ( υ ) d υ = ln ∣ G ( ω ) ∣ − ln ∣ G ( 0 ) ∣ = − σ 2 ω 2 2 . (1.6) \int\limits_0^\omega {{\textstyle{{\frac{{dG\left( \upsilon \right)}}{{d\upsilon }}} \over {G\left( \upsilon \right)}}}} d\upsilon = \ln \left| {G\left( \omega \right)} \right| - \ln \left| {G\left( 0 \right)} \right| = - \frac{{{\sigma ^2}{\omega ^2}}}{2}.\tag{1.6} 0∫ωG(υ)dυdG(υ)dυ=ln∣G(ω)∣−ln∣G(0)∣=−2σ2ω2.(1.6)
注意式 (1.6) 所使用的积分
∫ x 1 x 2 1 x d x = ln ∣ x 2 ∣ − ln ∣ x 1 ∣ \int\limits_{{x_1}}^{{x_2}} {\frac{1}{x}dx} = \ln \left| {{x_2}} \right| - \ln \left| {{x_1}} \right| x1∫x2x1dx=ln∣x2∣−ln∣x1∣
只有在 x 1 {x_1} x1 与 x 2 {x_2} x2 都大于 0 或都小于 0 时才存在。又因为
G ( 0 ) = ∫ − ∞ ∞ g ( x ) d x = 1 , (1.7)) G\left( 0 \right) = \int\limits_{ - \infty }^\infty {g\left( x \right)dx} = 1,\tag{1.7)} G(0)=−∞∫∞g(x)dx=1,(1.7))
于是可知 G ( ω ) > 0 G\left( \omega \right) > 0 G(ω)>0,并且有
ln G ( ω ) = − σ 2 ω 2 ⇒ G ( ω ) = e − σ 2 ω 2 2 . (1.8) \ln G\left( \omega \right) = - \frac{{{\sigma ^2}\omega }}{2} \Rightarrow G\left( \omega \right) = {e^{ - \frac{{{\sigma ^2}{\omega ^2}}}{2}}}.\tag{1.8} lnG(ω)=−2σ2ω⇒G(ω)=e−2σ2ω2.(1.8)
如果表示为高斯函数的形式,可得
G
(
ω
)
=
2
π
σ
1
2
π
(
1
/
σ
)
e
−
ω
2
2
(
1
/
σ
)
2
.
(1.9)
G\left( \omega \right) = \frac{{\sqrt {2\pi } }}{\sigma }\frac{1}{{\sqrt {2\pi } \left( {1/\sigma } \right)}}{e^{ - \frac{{{\omega ^2}}}{{2{{\left( {1/\sigma } \right)}^2}}}}}.\tag{1.9}
G(ω)=σ2π2π(1/σ)1e−2(1/σ)2ω2.(1.9)
因此,中心化高斯函数的傅里叶变换同样是一个高斯函数,只是没有进行积分的归一化,而且两者的方差刚好互为倒数。这是一个十分良好的性质,即高斯滤波作为一种低通滤波器不会在时域或频域产生任何类似于理想低通滤波器的震荡与过冲;并且当我们对信号进行高斯滤波时,并不需要将信号转换到频域,而直接在时域或者空域进行卷积即可,从而具有较低的计算复杂度。不过,高斯滤波的缺点在于其对于信号高频的衰减过于缓慢,而对于低频的衰减又过于严重,使得其通常被用于信号的平滑,而不是信号的高保真低频截止。不过,由于其低复杂度的优点,高斯滤波在图像信号处理中十分常用,包括但不限于降噪、边缘提取、图像融合等等。
2 数字信号处理中的高斯滤波
由于数字系统中我们无法直接利用连续高斯函数对信号进行滤波,所以通常需要对其采样离散化。而数字信号是模拟信号以归一化周期 T = 1 T = 1 T=1 进行采样的结果,所以高斯函数离散化时通常也以 1 为间隔,具体如下:
g [ n ] = 1 2 π σ e − n 2 2 σ 2 , n ∈ Z . (2.1) g\left[ n \right] = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{n^2}}}{{2{\sigma ^2}}}}},\;n \in \mathbb{Z}.\tag{2.1} g[n]=2πσ1e−2σ2n2,n∈Z.(2.1)
由于模拟信号的采样会不可避免地导致傅里叶变换的周期性延拓与叠加,即有
G d ( ω ) = ∑ k = − ∞ ∞ G a ( ω + 2 k π ) . (2.2) {G_d}\left( \omega \right) = \sum\limits_{k = - \infty }^\infty {{G_a}\left( {\omega + 2k\pi } \right)} .\tag{2.2} Gd(ω)=k=−∞∑∞Ga(ω+2kπ).(2.2)
其中 G a ( ω ) {G_a}\left( \omega \right) Ga(ω) 表示连续高斯函数的傅里叶变换, G d ( ω ) {G_d}\left( \omega \right) Gd(ω) 表示高斯函数离散后的离散时间傅里叶变换,而高斯函数的频谱是覆盖整个频域的,所以我们有必要讨论高斯函数在不同标准差参数下进行离散化时的频谱失真。除此以外,由于时域中的高斯滤波以卷积形式进行,为避免过高的复杂度通常会对式 (2.1) 中 n n n 的范围进行截断,这时相当于对时域施加了一个矩形窗,从而在频域引入类似于 sinc 函数的震荡问题,这个也是需要我们进行讨论的。
在第一节中我们已经知道,对于时域中标准差为 σ \sigma σ 的高斯函数,其傅里叶变换为
G ( ω ) = e − σ 2 ω 2 2 . (2.3) G\left( \omega \right) = {e^{ - \frac{{{\sigma ^2}{\omega ^2}}}{2}}}.\tag{2.3} G(ω)=e−2σ2ω2.(2.3)
因为模拟信号以归一化周期 T = 1 T = 1 T=1 进行采样时,会导致模拟信号的频谱以频率 ω T = 2 π {\omega _T} = 2\pi ωT=2π 为周期进行延拓,这时 ω > ω T / 2 = π \omega > {\omega _T}/2 = \pi ω>ωT/2=π 的分量就会与低频部分发生叠加混合。因为高斯函数频谱的形状是由 σ \sigma σ 唯一决定的,如果我们希望在高斯函数离散化时尽量避免频谱混叠的问题,就需要选择合适的 σ \sigma σ 值。定量化地,如果我们要求 G ( ± π ) < α G\left( { \pm \pi } \right) < \alpha G(±π)<α,那么 σ \sigma σ 需满足以下条件:
e − σ 2 ω 2 2 < α ⇒ σ > 1 π 2 ln 1 α . (2.4) {e^{ - \frac{{{\sigma ^2}{\omega ^2}}}{2}}} < \alpha \Rightarrow \sigma > \frac{1}{\pi }\sqrt {2\ln \frac{1}{\alpha }} .\tag{2.4} e−2σ2ω2<α⇒σ>π12lnα1.(2.4)
以 α = 0.1 \alpha = 0.1 α=0.1 为例,此时有 σ > 0.683 \sigma > 0.683 σ>0.683,对于日常使用的 3x3 与 5x5 高斯滤波这个条件其实都是能够满足的,因为如 OpenCV 里所使用的默认高斯函数标准差的计算公式如下:
σ = 0.3 ∗ ( 0.5 ∗ ( L − 1 ) − 1 ) + 0.8 , (2.5) \sigma = 0.3*\left( {0.5*\left( {L - 1} \right) - 1} \right) + 0.8,\tag{2.5} σ=0.3∗(0.5∗(L−1)−1)+0.8,(2.5)
当 L = 3 L = 3 L=3 时即有 σ = 0.8 > 0.683 \sigma = 0.8 > 0.683 σ=0.8>0.683。不过,当高斯滤波窗口过小时,我们更需要关心的是由于时域矩形窗所引入频域震荡的问题。
由于离散信号的离散时间傅里叶变换 (DTFT) 仍然是连续函数,且根据式 (2.2) 可知其由一个无穷级数所定义,所以具体的形式不好直接计算。为了直观了解不同标准差参数以及滤波窗口长度对高斯函数离散化的影响,我们可以利用离散傅里叶变换 (DFT) 来间接地获得频谱混叠后的分布图像,这是因为离散傅里叶变换本质上是有限长离散序列的离散时间傅里叶变换频谱在
[
0
,
2
π
)
[0,2\pi )
[0,2π) 上等间隔采样的结果,只要参与离散傅里叶变换的序列长度不小于离散序列的有效长度,即参与离散傅里叶变换的序列区间之外的部分为零或几乎为零,则离散傅里叶变换的结果与离散时间傅里叶变换的结果是可相互换算的。要注意的是,虽然在 OpenCV 中我们可通过 getGaussianKernel(ksize, sigma) 函数来获取长度为 ksize 的标准差为 sigma 的一维高斯滤波核,但这里有个容易忽略的问题是 OpenCV 会对所得高斯核所有元素之和进行归一化,使得频谱中的直流系数始终为 1,避免信号的直流分量发生改变,但是我们一般所讨论的离散时间傅里叶变换只需要对原始连续信号进行采样,而无需对采样后的序列之和进行归一化,因此两者所得的频谱可能存在着一个缩放比例的差异,后面我们会给出两者的区别。除此以外,OpenCV 还可能会对高斯核中部分数字进行微调,使其能够通过乘以某个 2 的幂而成为整数,方便计算机的移位运算,这里不过多讲述。
注意,高斯滤波窗口的长度与离散傅里叶变换所使用的序列长度是两个概念。滤波窗口长度决定了离散序列的有效长度,而离散傅里叶变换的长度决定了频域中 [ 0 , 2 π ) [0,2\pi ) [0,2π) 上的采样点数,正常来说离散傅里叶变换的长度不小于离散序列的有效长度,且离散傅里叶变换的长度越大,我们在绘制频谱曲线时就能更加平滑,更加接近于离散时间傅里叶变换的真实曲线。以长度为 5 的高斯滤波核为例,常用的整数化序列为 [1, 4, 6, 4, 1],这里为了方便先不进行归一化。因为离散傅里叶变换可通过 FFT 算法进行加速,而 FFT 通常要求变换长度为 2 的幂,我们这里以 8 为例,那么输入到 FFT 的离散序列应该为 [6, 4, 1, 0, 0, 0, 1, 4]。注意这里实际上是对原始高斯核序列以变换长度 8 进行了周期性延拓,并以高斯核中心为起点截取一个变换周期的结果。这是因为高斯核的中心才对应着时域上的零点,如果不按照以上的方式处理,则相当于在时域中引入了时移,并在频域中引入相位差,不过频域的幅度是不受影响的,所涉及的知识可查阅相关资料或者我过去的博客,这里不细说。
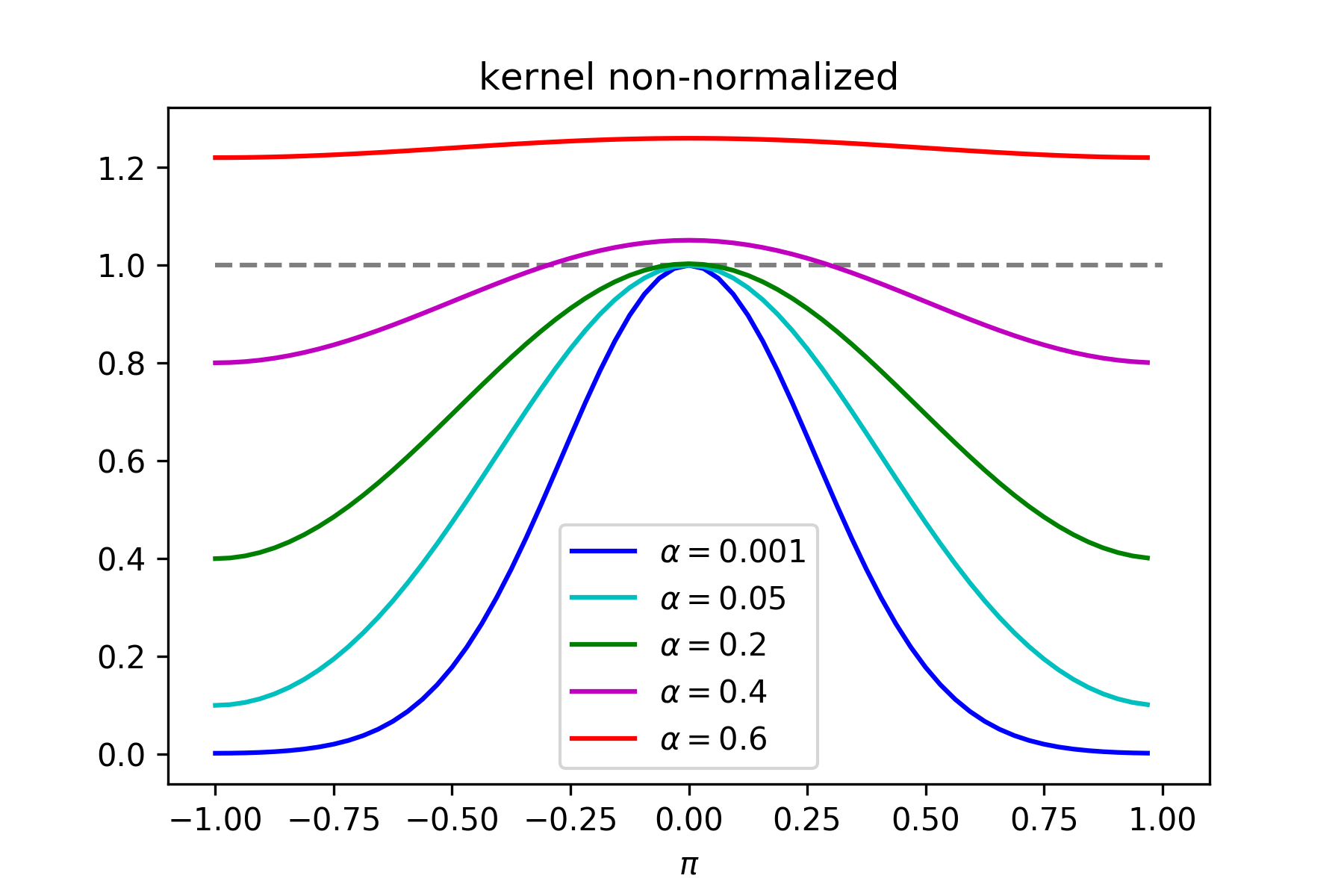
如图 1 所示,当我们根据式 (2.4) 的条件对相应标准差的连续高斯函数进行采样离散化后,所得 FFT 频谱总体上还是保持着高斯函数的形态,但又存在着不同程度的失真。随着 α \alpha α 参数的增大, σ \sigma σ 会逐渐减小趋近于 0,使得高斯函数逐渐趋近于狄拉克函数,频谱也不断向高频延伸,在采样后存在着更严重的混叠失真。当 α \alpha α 比较小时,根据式 (2.2) 大致只有两个高斯函数频谱的叠加,所以有 G ( ± π ) ≈ 2 α G\left( { \pm \pi } \right) \approx 2\alpha G(±π)≈2α,并且直流分量也基本没有变化;而当 α \alpha α 增大后,更多的高斯函数频谱叠加在一起,使得 G ( ± π ) G\left( { \pm \pi } \right) G(±π) 要明显高于 2 α 2\alpha 2α,且直流分量也因为混叠的原因有所增加。不过,正如我们前面所讨论的,只要 σ > 0.683 \sigma > 0.683 σ>0.683 即有 α < 0.1 \alpha < 0.1 α<0.1,而这个条件在我们常用的高斯滤波核中都是满足的,因此不必过分担心。除此以外,图 1 所示频谱是采样后未进行离散序列之和归一化的结果,在进行归一化后,它们的直流分量将保持为 1 不变,而其他分量则存在着一个缩放比例的关系,具体如图 2 所示。解决了高斯函数离散化的频谱混叠问题后,接下来我们就要讨论高斯离散序列截断长度对频谱的影响。

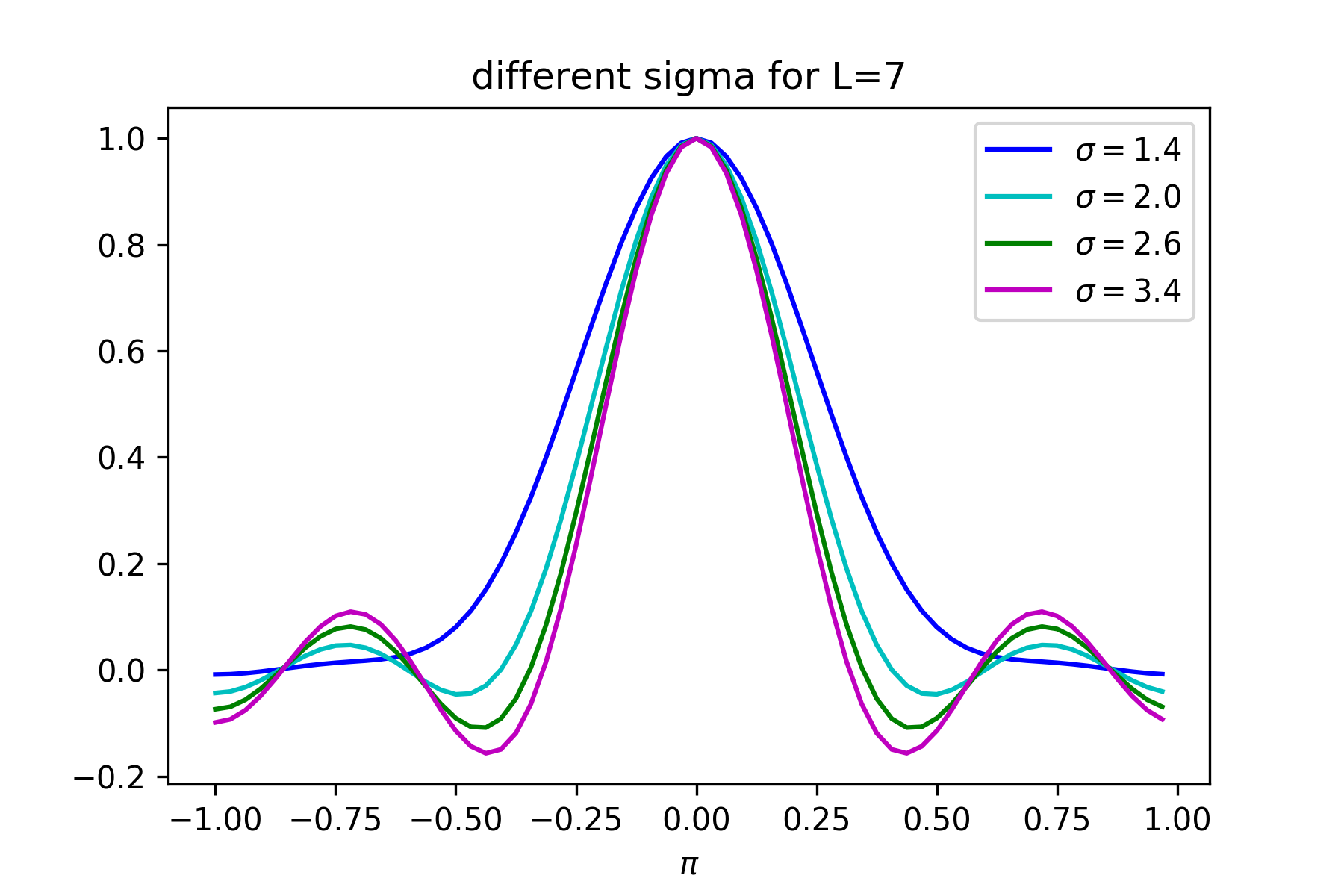
在式 (2.5) 中,我们可知给定一个高斯核长度,OpenCV 可以自动计算一个默认的标准差,图 3 展示了一些常用高斯核长度在默认标准差下所对应的频谱。可以看到,在默认标准差下,离散化的高斯函数基本不发生频谱混叠。但是随着长度的增加,频谱在高频出出现了轻微的震荡,这是由于随着标准差的增加,高斯函数下降更加平缓,使得窗口的截断效应更加明显,从而在频域中引入了 sinc 函数的震荡问题。具体的公式推导这里不细究,但从图 3 可看出在默认标准差下,频谱的震荡问题还是基本可以忽略的。为了更深刻地了解窗口截断的问题,图 4 展示了在高斯核长度固定为 7 时,通过增加标准差值对高斯函数频谱的影响。可以看到,随着标准差的增大,频谱的震荡问题愈发严重,因此我们在进行高斯核的选择时,必须根据长度选择合适的标准差值,否则可能引入一些不必要的失真。但总的来说,直接在 OpenCV 中使用默认标准差就已经是一个不错的选择,从这我们也能领会到 OpenCV 对于实现细节的质量把控。

3 测试脚本
这里给出本文用于生成频谱图片的 Python 脚本,有兴趣可自行下载、修改、运行。
# -*- coding: utf-8 -*-
import numpy as np
import cv2
import matplotlib.pyplot as plt
def get_gauss_fft(ksize, sigma, fft_size, from_cv=True):
kr = ksize // 2
if from_cv:
kern = cv2.getGaussianKernel(ksize, sigma).reshape(-1)
else:
kern = np.exp(-np.arange(-kr, kr+1)**2 / (2 * sigma**2))
kern = kern / (np.sqrt(2 * np.pi) * sigma)
gauss = np.zeros(fft_size, dtype='float64')
gauss[:kr+1] = kern[kr:]
gauss[-kr:] = kern[:kr]
gauss_fft = np.fft.fft(gauss)
gauss_fft = np.fft.fftshift(gauss_fft)
gauss_fft = np.real(gauss_fft)
return gauss_fft
def get_gauss_fft_alpha(ksize, alpha, fft_size, from_cv=False):
sigma = np.sqrt(-2 * np.log(alpha)) / np.pi
return get_gauss_fft(ksize, sigma, fft_size, from_cv)
if __name__ == '__main__':
fft_size = 64
omega = np.linspace(0, 1, fft_size//2+1, endpoint=True)
omega = np.hstack((-omega[::-1], omega[1:-1]))
plt.figure()
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.001, fft_size, False), 'b')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.05, fft_size, False), 'c')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.2, fft_size, False), 'g')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.4, fft_size, False), 'm')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.6, fft_size, False), 'r')
plt.legend([r'$\alpha=0.001$', r'$\alpha=0.05$', r'$\alpha=0.2$', r'$\alpha=0.4$', r'$\alpha=0.6$'])
plt.xlabel(r'$\pi$')
plt.title('kernel non-normalized')
plt.hlines(1, -1, 1, 'k', '--', alpha=0.5)
plt.savefig('gauss_sampled.png', dpi=300)
plt.figure()
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.001, fft_size, True), 'b')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.05, fft_size, True), 'c')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.2, fft_size, True), 'g')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.4, fft_size, True), 'm')
plt.plot(omega, get_gauss_fft_alpha(fft_size-1, 0.6, fft_size, True), 'r')
plt.legend([r'$\alpha=0.001$', r'$\alpha=0.05$', r'$\alpha=0.2$', r'$\alpha=0.4$', r'$\alpha=0.6$'])
plt.xlabel(r'$\pi$')
plt.title('kernel normalized to 1')
plt.savefig('gauss_sampled_norm.png', dpi=300)
plt.figure()
plt.plot(omega, get_gauss_fft(3, 0, fft_size, True), 'b')
plt.plot(omega, get_gauss_fft(5, 0, fft_size, True), 'c')
plt.plot(omega, get_gauss_fft(9, 0, fft_size, True), 'g')
plt.plot(omega, get_gauss_fft(13, 0, fft_size, True), 'm')
plt.legend(['L=3', 'L=5', 'L=9', 'L=13'])
plt.xlabel(r'$\pi$')
plt.title('OpenCV default kernel')
plt.savefig('gauss_default.png', dpi=300)
ksize = 7
sigma = 0.3 * ((ksize - 1) * 0.5 - 1) + 0.8
#ideal = np.exp(-(sigma * omega * np.pi)**2 / 2) # analog fourier
plt.figure()
plt.plot(omega, get_gauss_fft(ksize, sigma, fft_size, True), 'b')
plt.plot(omega, get_gauss_fft(ksize, sigma+0.6, fft_size, True), 'c')
plt.plot(omega, get_gauss_fft(ksize, sigma+1.2, fft_size, True), 'g')
plt.plot(omega, get_gauss_fft(ksize, sigma+2.0, fft_size, True), 'm')
plt.legend([r'$\sigma={:.1f}$'.format(sigma), r'$\sigma={:.1f}$'.format(sigma+0.6),
r'$\sigma={:.1f}$'.format(sigma+1.2), r'$\sigma={:.1f}$'.format(sigma+2.0)])
plt.xlabel(r'$\pi$')
plt.title('different sigma for L={}'.format(ksize))
plt.savefig('gauss_sigma.png', dpi=300)
plt.show()




![[语义分割] ASPP不同版本对比(DeepLab、DeepLab v1、DeepLab v2、DeepLab v3、DeepLab v3+、LR-ASPP)](https://img-blog.csdnimg.cn/08d74f7c54de4c45b4344eab71438481.png#pic_center)