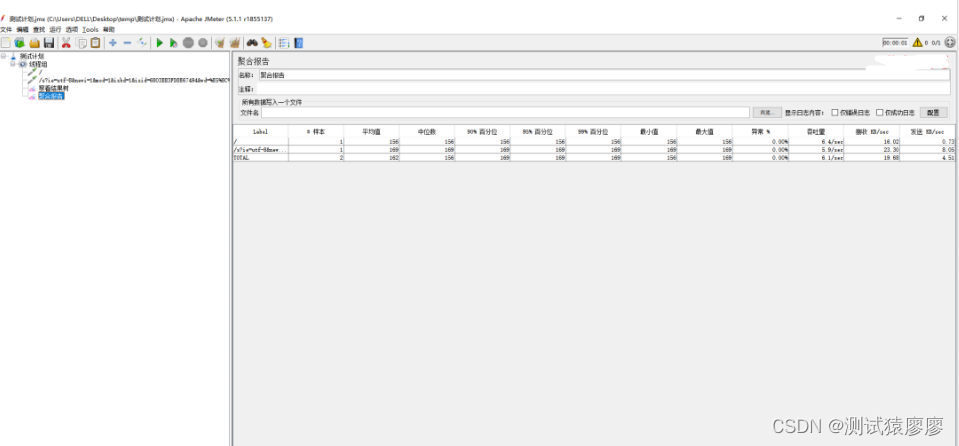
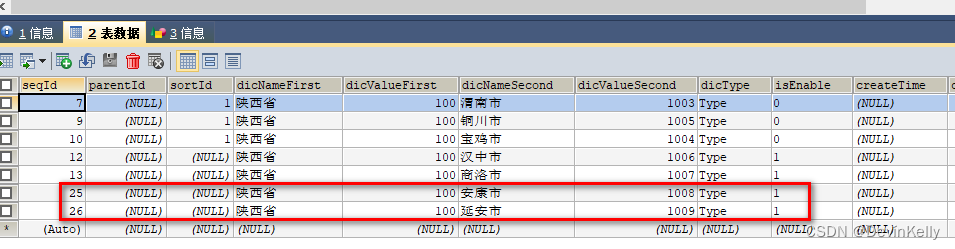
简述

形式逻辑：

1. 识别题型：逻辑符号表达及标志词：联假言符号化+特殊命题“除非否则”；
2. 五大关系：矛盾、等价、包含、至少有一真、至少有一假；【通过“关系”，串联起“假联选”言】

识别题型：逻辑符号表达及标志词

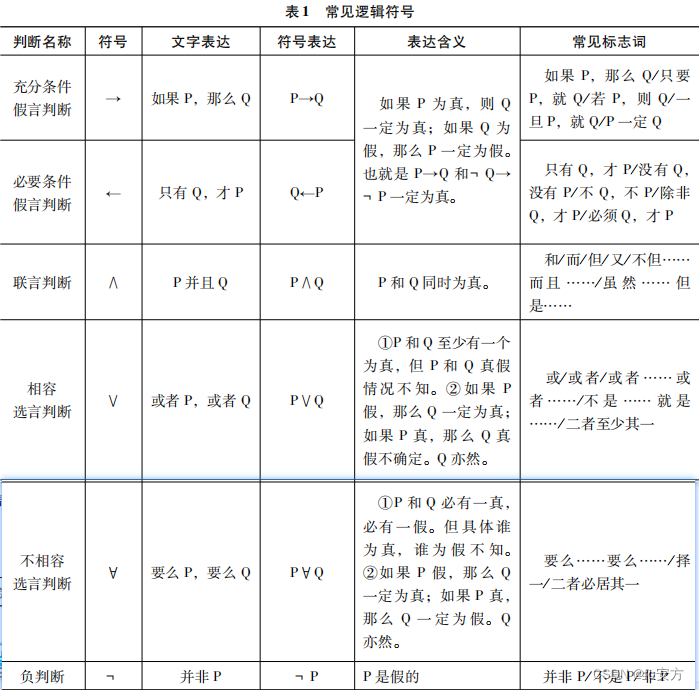
在应试时，“ → ” 和 “ ← ”的符号一般都习惯用 “ → ” 来进行统一表达，因此P → Q和Q ← P是等价的，也就意味着，“如果Р，那么Q” = “只有Q，才P”，都可以用“P → Q”来表达。

请将下列语句用符号来表达。
（1）知无不言，言无不尽。
（2）德才兼备。
（3）虽然你成绩不太好，但是你也不能自暴自弃。
（4）宋玉和潘安都是男神。
（5）他既大方又稳重。
（6）考研不但时间要抓紧，而且效率也要高。
（7）他一面若无其事，一面暗自神伤。
（8）夕阳西下，断肠人在天涯。
（9）可能晚上吃米饭，也可能吃蔬菜沙拉。
（10）一个成功人士的才华和气质至少得有一个特别出众。
（11）这次没考好，也许是题目太难，也许是状态不佳。
（12）学习委员从张三和李四择一担任。
（13）但凡成功者天赋和努力二者必居其一。
（14）人要真诚，也要善良。
（15）明天或者刮风，或者下雨。
（16）要么考研，要么考公务员。
（17）如果找到真爱，那么懂得真爱。
（18）若找到真爱，则懂得真爱。
（19）一旦找到真爱，则懂得真爱。
（20）只要找到真爱，就懂得真爱。
（21）必须懂得真爱，才能找到真爱。
（22）只有懂得真爱，才能找到真爱。
（23）不懂得真爱，不能找到真爱。
（24）除非懂得真爱，才能找到真爱。
（25）除非懂得真爱，否则不能找到真爱。
（26）除非懂得真爱，否则能找到真爱。
（27）除非不懂得真爱，否则能找到真爱。
（28）找到真爱，除非懂得真爱。
（29）懂得真爱，否则找到真爱。
（30）并非张珊是成功人士。

【精点解析】
(1)表示同时为真，即：知无不言∧言无不尽。
(2)根据标志词“兼备”表示“且”，即：德 ∧ 才。
(3）根据标志词“虽然……但是……”表示“且”，即：成绩不太好 ∧ 不能自暴自弃。
(4)根据标志词“都是”表示“且”，即：宋玉是男神 ∧ 潘安是男神。
(5）根据标志词“既……又……”表示“且”，即：大方 ∧ 稳重。
(6）根据标志词“不但……而且……”表示“且”，即：考研时间要抓紧 ∧ 效率要高。
(7）根据标志词“一面……一面……”表示“且”，即：他若无其事 ∧ 暗自神伤。
(8)表示同时为真，即：夕阳西下 ∧ 断肠人在天涯。
(9）根据标志词“可能……也可能……”表示“或”，可能存在晚上同时吃米饭和蔬菜沙拉的可能，表示P V Q，即：晚上吃米饭 V 晚上吃蔬菜沙拉。
(10）根据标志词“至少有一个”表示“或”，即：一个成功人士的才华特别出众 V 气质特别出众。
(11)根据标志词“也许……也许……”表示“或”，即：这次没考好，题目太难 V 状态不佳。
(12）根据标志词“择一”表示“要么……要么……”，即：张三担任学习委员 ∀ 李四担任学习委员。
(13）根据标志词“必居其一”表示“要么……要么……”，即：成功者有天赋 ∀ 有努力。
(14)根据标志词“也”表示“且”，即：人要真诚 ∧ 人要善良。
(15）根据标志词“或者……或者……”表示“或”，即：明天刮风 V 明天下雨。
(16）根据标志词“要么……要么……”即：考研 ∀ 考公务员。
(17)根据标志词“如果P，那么Q”表示“P→Q”，即：找到真爱→懂得真爱。
(18）根据标志词“若P，则Q”表示“P→Q”，即：找到真爱→懂得真爱。
(19)根据标志词“一旦P，就Q”表示“P→Q”，即：找到真爱→懂得真爱。
(20）根据标志词“只要P，就Q”表示“P→Q”，即：找到真爱→懂得真爱。
(21）根据标志词“必须Q，才P”表示“P→Q”，即：能找到真爱→懂得真爱。
(22）根据标志词“只有Q，才P”表示“P→Q”，即：能找到真爱→懂得真爱。
(23）根据标志词“不Q，不P”表示“P→Q”，即：能找到真爱→懂得真爱。
(24）根据标志词“除非Q，才P”表示“P→Q”，即：能找到真爱→懂得真爱。
(25）根据标志词“除非Q，否则不P”表示“┐Q→┐P”，即：不懂得真爱→不能找到真爱。
(26）根据标志词“除非Q，否则P”表示“┐Q→P”，即：不懂得真爱→能找到真爱。
(27）根据标志词“除非Q，否则P”表示“┐Q→P”，即：懂得真爱→能找到真爱。
(28）根据标志词“P，除非Q”表示“┐P→Q”，即：找不到真爱→懂得真爱。
(29）根据标志词“P，否则Q”表示“┐P→Q”，即：找不到真爱→懂得真爱。
(30）根据标志词“并非P”，即：┐张珊是成功人士 = 张珊不是成功人士。

难点：除非Q，否则P

考生注意：“→”表示的假言判断有常见的三种特殊结构，如下：

1. 除非Q，否则P。“否则”的逻辑表达所包含的两个词“否”和“则”（除非，除表示否定，非表示否定，双重否定表肯定），正好分别对应于“┐”和“→”。因此“除非Q，否则P”的意思是“如果否定Q，则P”，即┐Q→P。同理可知，“除非Q，否则不P”=┐Q→┐P。如(25)(26)(27)小题。
2. P，否则Q。这样的结构需要记住，“否”是否“否则”前面的断定；“则”是则“否则”后面的断定。因此“P，否则Q”的意思也是“如果否定Р，则Q”，即┐P→Q。如(29)小题。
3. P，除非Q。这样的结构其实是省略了“否则”，补充完整应该是“除非Q，否则P”。意思是“如果否定Q，则P”，即┐P→Q。如(28)小题。由于假言判断推理可取逆否等价，故：┐Q→P=┐P→Q； ┐Q→┐P = P→Q。考生注意将( 17) ~ (29)小题综合起来理解。

形式逻辑五大关系

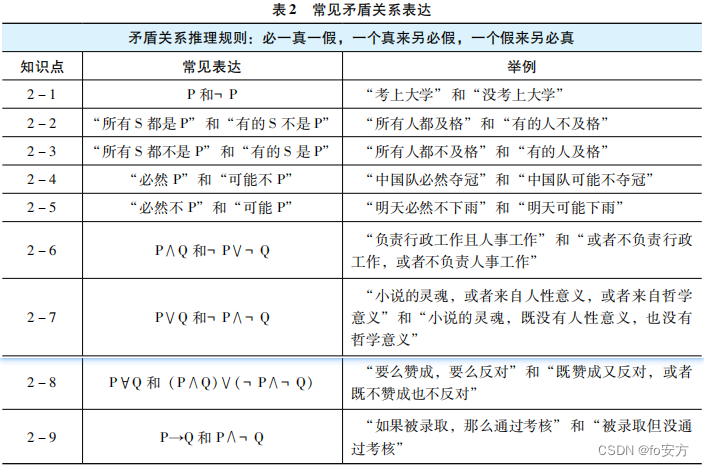
一、矛盾关系

二、等价关系

常见等价关系表

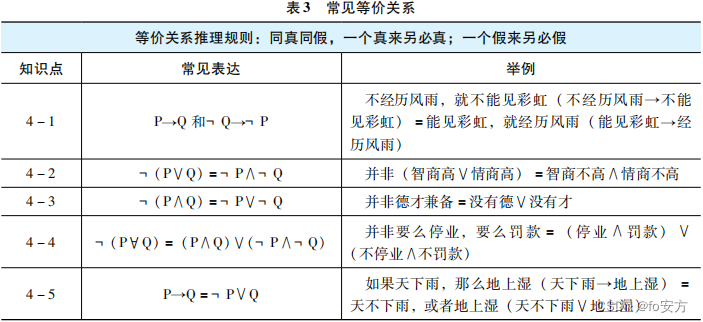
等价公式

1. 假言
   （1）$P\to Q=┐Q\to ┐P$
   （2）$P\leftrightarrow Q=(P\wedge Q)\vee (┐P\wedge ┐Q)$
   （3）$┐(P\leftrightarrow Q)=(P\wedge ┐Q)\vee (┐P\wedge Q)$
2. 联言选言
   （1）$┐(P\vee Q)=┐P\wedge ┐Q$
   （2）$┐(P\wedge Q)=┐P\vee ┐Q$
   （3）$P\vee Q=(P\wedge ┐Q)\vee (┐P\wedge Q)$
   （4）$┐(P\vee Q)=(P\wedge Q)\vee (┐P\wedge ┐Q)$
3. 或则转化
   （1）$P\vee Q=┐P\to Q=┐Q\to P$
   （2）$P\to Q=┐(P\wedge ┐Q)=┐P\vee Q$
   注意：若出现“或”，且题干不涉及真假，优先将“或”变“推”。题干涉及真假，若没有“推”与“且”这一组矛盾，优先将“则”转成“或”。
4. 递推推理
   $A\to B，B\to C，所以A\to B\to C$
5. 做题思路
   观察“→”的个数
   （1）1个，考查自身，考查逆否等价，或者逻辑标志词的转化。
   （2）多个，能串则串，比照选项，注意首尾；不能串，一一比照选项，往往是某一句的等值。

三、包含关系

∩ ∪ ∧ ∨ ⊃ ⊂ ∅ ⟺ ┐ ∀ ∞ σ ∈ ± ∓ ↔

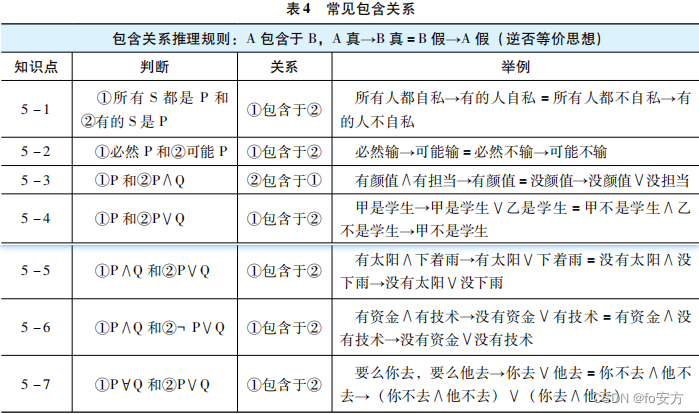
考生注意：
1.“有的S是P”表示至少有一个S是P，至多全部的S都是P，因此“所有S都是P”是“有的S是P”为真时的一种可能，故“所有S都是P”包含于“有的S是P”。
2．同理可知，“可能P”表示发生概率大于0、小于等于100%，因此，“必然P”是“可能P”为真时的一种可能，故“必然P”包含于“可能P”。

四、至少有一真的关系

若A和B属于至少有一真的关系，就意味着A和B至少有一个为真，可能有一个真，也可能两个都是真的；如果一个是真，那么另一个无法判断；如果一个是假，那么另一个为真。

至少有一假的关系

若A和B属于至少有一假的关系，就意味着A和B至少有一个为假，可能有一个假，也可能两个都是假的；如果一个是假，那么另一个无法判断；如果一个是真，那么另一个为假。