3D空间点到直线的距离
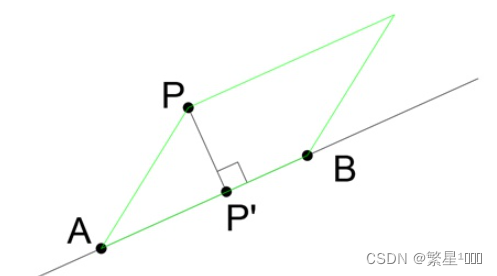
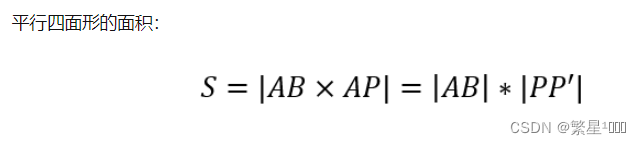
3D空间点到直线的距离
3D空间的曲率
三维空间有三个基本元素,点,线,面。那么曲率是如何定义的呢?
点的曲率?
线的曲率?
面的曲率?
法曲率
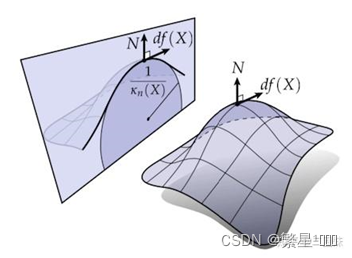
设曲面上的曲线在某一点处的切向量为df(X),曲面在这一点处的法向量为N。则曲线的法曲率就是曲线在df(X)和N张成的平面上的投影曲线的曲率。
在曲面上取一点E,曲面在E点的法线为z轴,过z轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E点有一个曲率半径。不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。
主曲率
曲面的每个方向都有法曲率,那么就有最大最小的法曲率,这个最大最小值就是主曲率,对应的曲线在这点的切线方向就是主曲率方向。这两个方向是垂直的。
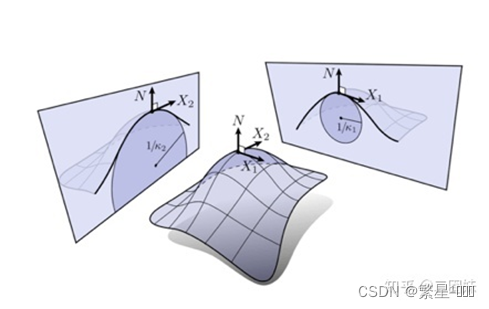
根据主曲率的不同,可以对曲面分类
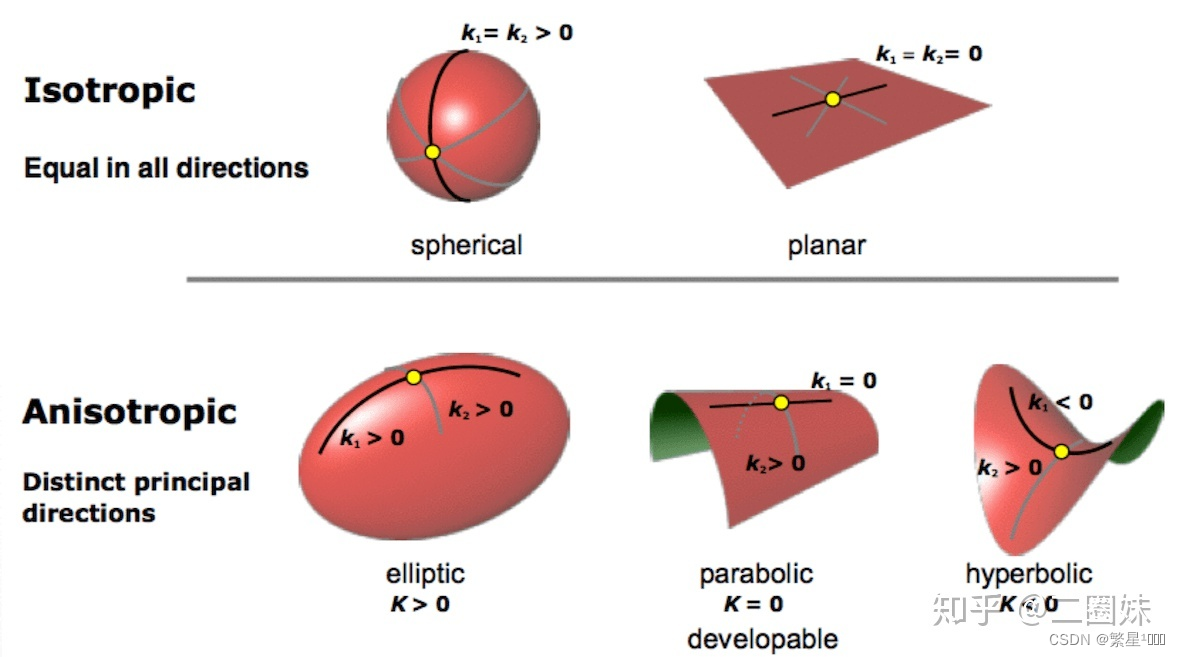
高斯曲率
微分几何中,曲面上一点的高斯曲率是该点主曲率κ1和κ2的乘积。
K
=
k
1
∗
k
2
K= k_1*k_2
K=k1∗k2
**它是曲率的内在度量,度量的是曲面内在的弯曲程度。**也即,它的值只依赖于曲面上的距离如何测量,而不是曲面如何嵌入到空间。一个曲面做任何非拉伸的变换都不会改变它的高斯曲率,如平面高斯曲率为0,把它弯曲成圆柱,其高斯曲率也还是为0。
三维网格高斯曲率计算公式:
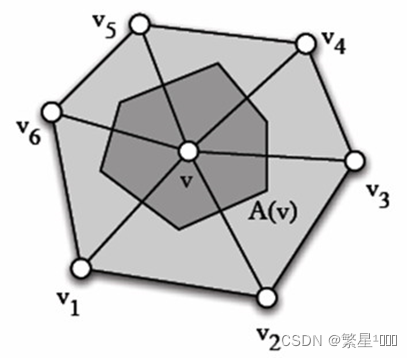
K ( v ) = 1 A ( v ) ( 2 π − ∑ v i ∈ N 1 ( v ) θ i ) K(v) = \frac{1}{A(v)}(2\pi - \sum_{v_i\in{ N_1}(v)}\theta_i) K(v)=A(v)1(2π−vi∈N1(v)∑θi)
这个公式的几何意义是比较直观的,2*Pi-该点邻域三角形对应的角度和,再除以相应区域的面积,就刻画了该点曲面的弯曲程度。
平均曲率
微分几何中,曲面上一点的平均曲率是该点主曲率κ1和κ2的平均值。
K
=
k
1
+
k
2
2
K=\frac{k_1 + k_2}{2}
K=2k1+k2
它度量了曲面在空间中的弯曲程度。比如平面弯曲成圆柱后,其平均曲率就不为0了。
高斯曲率
如何简明地解释曲率(curvature)?
法曲率、主曲率、高斯曲率、平均曲率
三角网格表面高斯曲率的计算与可视化