数据结构-二叉树

news2024/11/24 2:18:52

数据结构-二叉树

    • 二叉树的概念
    • 二叉树的遍历分类
  • 建立二叉树，并遍历
    • 二叉树的最小单元
    • 二叉树的最小单元初始化
    • 初始化二叉树
    • 前序遍历的实现
    • 中序遍历的实现
    • 后序遍历的实现
    • 计算节点的个数
    • 计算树的深度
    • 求第k层的个数
    • 查找二叉树的元素
    • 分层遍历
  • 全部代码如下

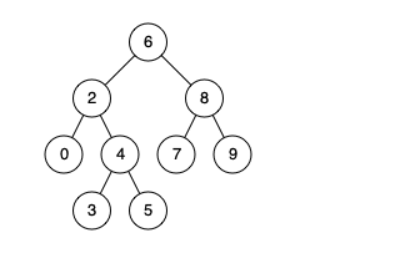
二叉树的概念

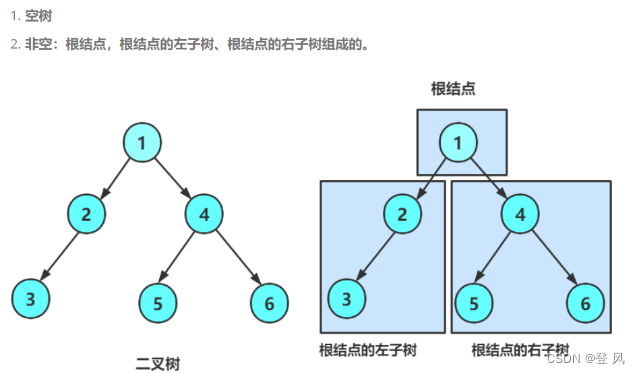
在这里插入图片描述

二叉树的遍历分类

有前序遍历，中序遍历，后序遍历和层序遍历
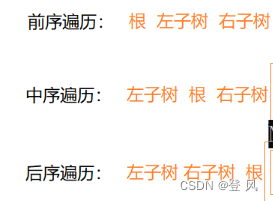
在这里插入图片描述

规则：

1.遇到根可以直接访问根
2.遇到左子树，右子树，不可以直接访问，要将其看作一颗新的二叉树，按遍历规则，再次循环，直至左子树或右子树为空，则可访问空。

前序遍历
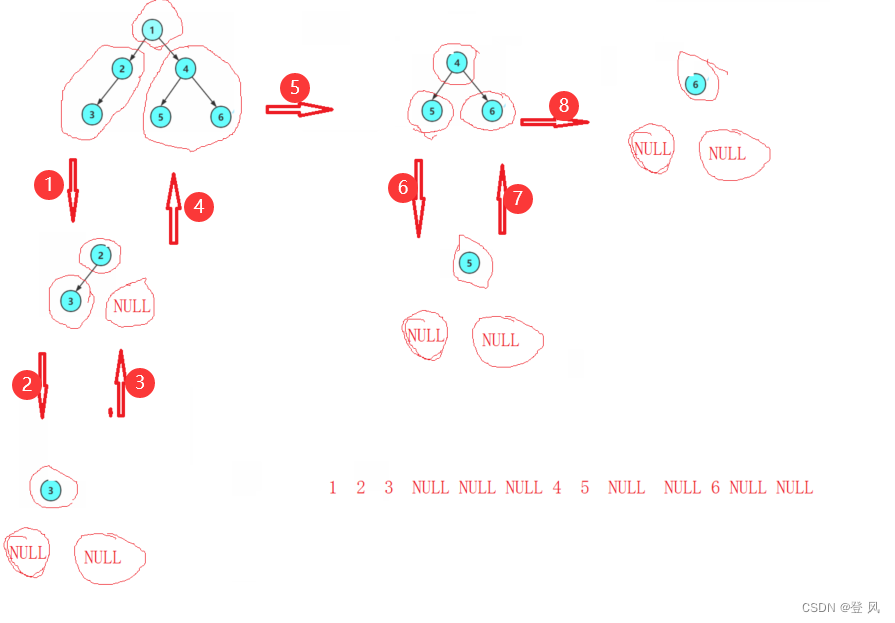
在这里插入图片描述
中序遍历和后序遍历
中序遍历：
三者访问根的时机不同

层序遍历：一层一层的进行

1 2 4 3 5 6

建立二叉树，并遍历

二叉树的最小单元

根，左子树和右子树

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

二叉树的最小单元初始化

BTNode* BuyNode(BTDataType x)
{
	BTNode* node=(BTNode*)malloc(sizeof(BTNode));
	if (node==NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

初始化二叉树

BTNode* CreatTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;

	node2->left = node3;

	node4->left = node5;
	node4->right=node6;

	return node1;
}

前序遍历的实现

函数的回归条件为root为空，或者函数正常结束
按照顺序依次为：根，左子树，右子树

void PreOrder(BTNode* root)
{
	if (root==NULL)
	{
		printf("NULL ");
		return;
	}
	//root,left,right
	printf("%d ",root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

递归调用展开图
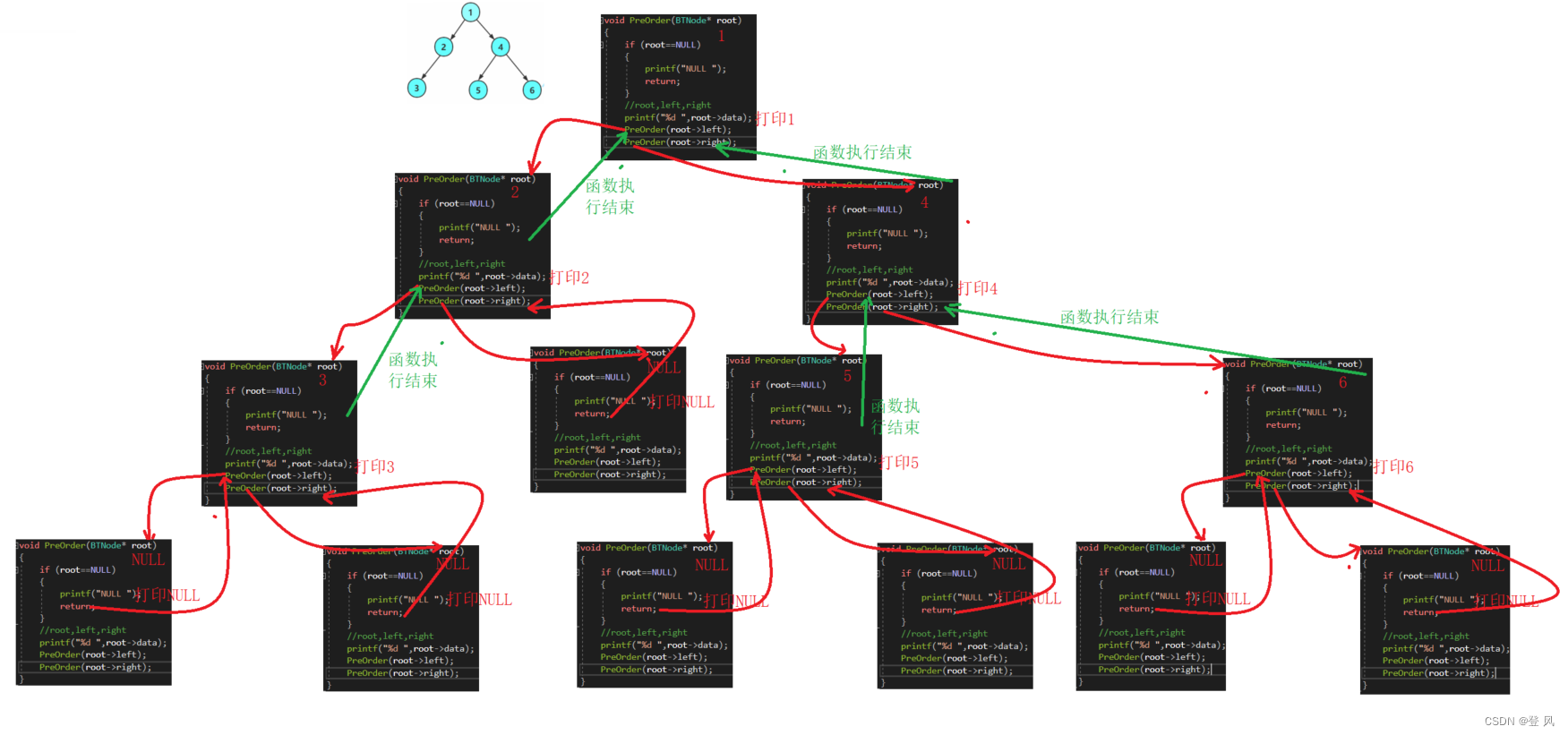
在这里插入图片描述

结果如下：
在这里插入图片描述

中序遍历的实现

函数的回归条件为root为空，或者函数正常结束
按照顺序依次为：左子树，根，右子树

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

后序遍历的实现

函数的回归条件为root为空，或者函数正常结束
按照顺序依次为：左子树，右子树，根

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

计算节点的个数

利用分治法求节点的个数，只有节点存在时，才会+1，并返回下层的统计个数
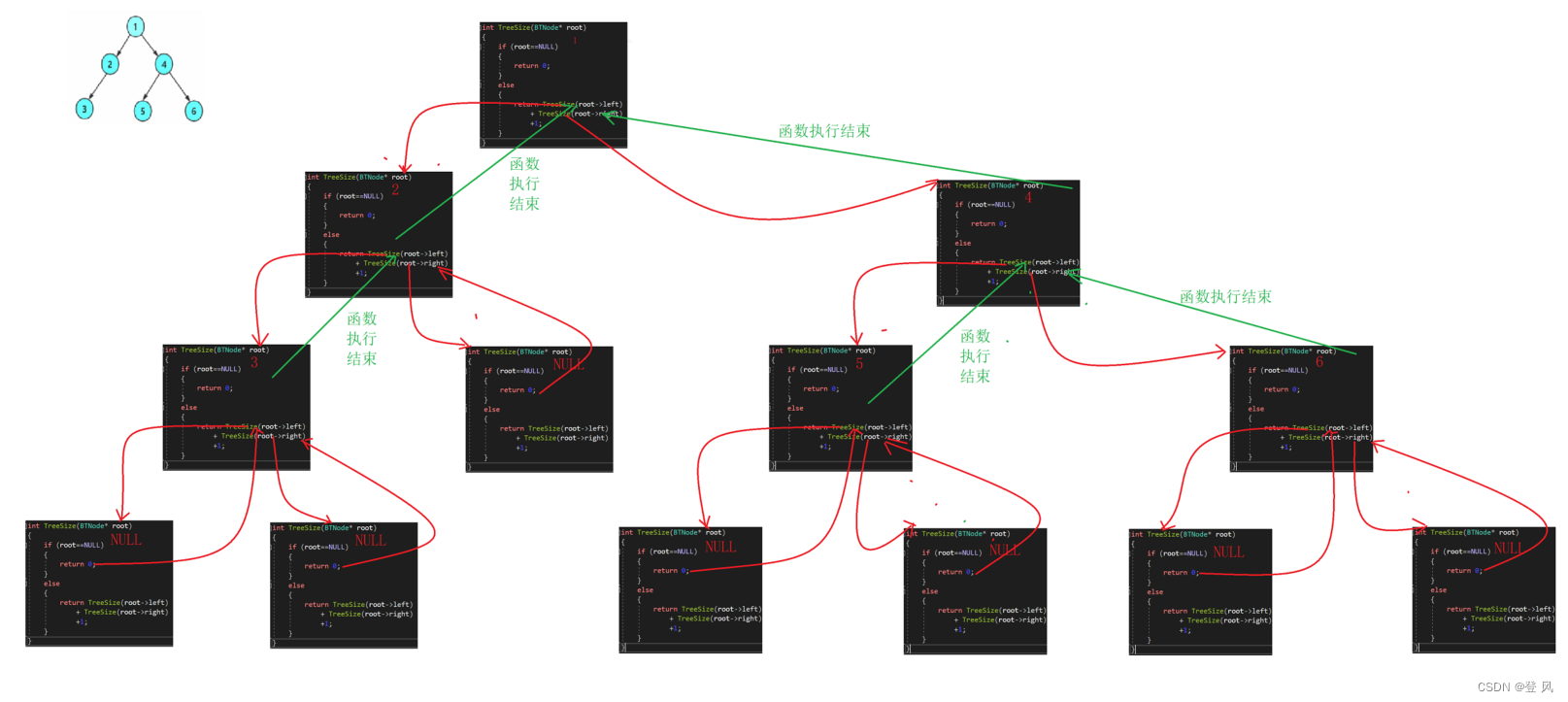
在这里插入图片描述

int TreeSize(BTNode* root)
{
	if (root==NULL)
	{
		return 0;
	}
	else
	{
		return TreeSize(root->left) 
			+ TreeSize(root->right)
			+1;
	}
}

执行结果如下：
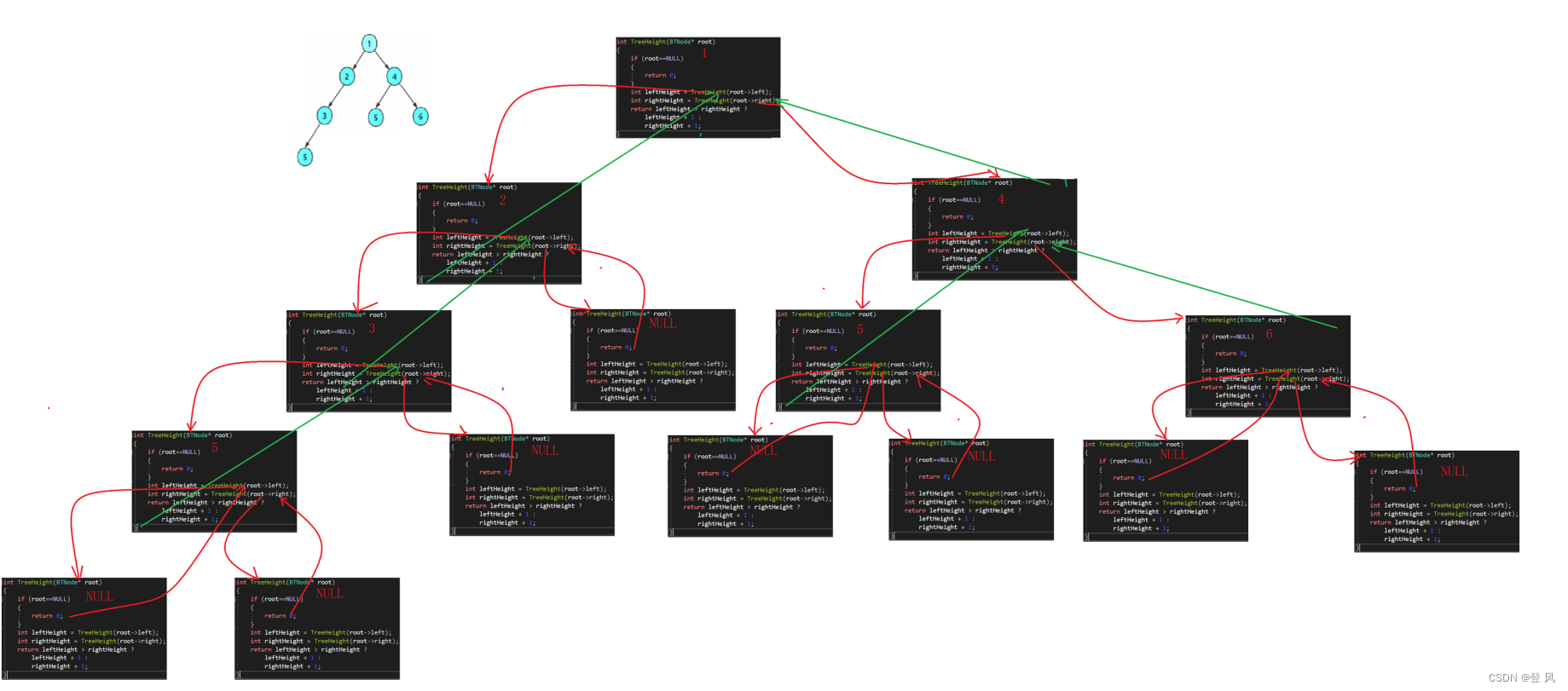
在这里插入图片描述

计算树的深度

在这里插入图片描述

int TreeHeight(BTNode* root)
{
	if (root==NULL)
	{
		return 0;
	}
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);
	return leftHeight > rightHeight ?
		leftHeight + 1 :
		rightHeight + 1;
}

代码执行结果如下：
在这里插入图片描述

求第k层的个数

在这里插入图片描述

int TreeLevel(BTNode* root,int k)
{
	if (root==NULL)
	{
		return 0;
	}

	if (k==1)
	{
		return 1;
	}

	return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}

运行结果如下:
在这里插入图片描述

查找二叉树的元素

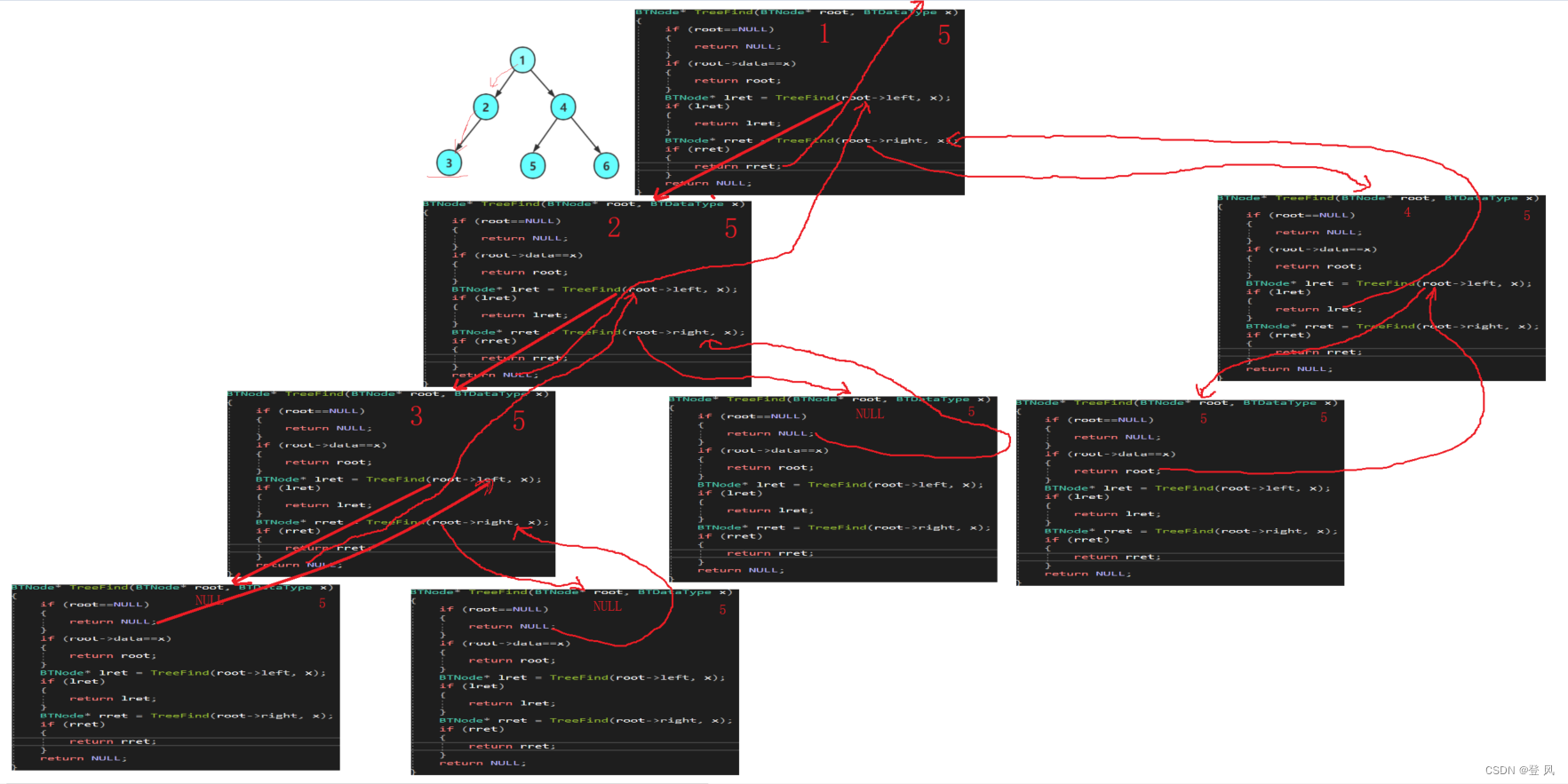
在这里插入图片描述

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root==NULL)
	{
		return NULL;
	}
	if (root->data==x)
	{
		return root;
	}
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
	{
		return lret;
	}
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
	{
		return rret;
	}
	return NULL;
}

结果如下：
在这里插入图片描述

分层遍历

利用队列，先将根push，进入循环，可pop，再将层子节点push，依次循环。安照队列先进先出的原则，可实现分层打印

void LevelOrder(BTNode* root)
{
	Quene q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q,root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->data);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}

	QueueDestroy(&q);
}

结果如下：

在这里插入图片描述
判断是否为完全二叉树

bool TreeComplete(BTNode* root)
{
	Quene q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front==NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

全部代码如下

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include "Queue.h"

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node=(BTNode*)malloc(sizeof(BTNode));
	if (node==NULL)
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

BTNode* CreatTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	//BTNode* node6 = BuyNode(6);

	//node1->left = node2;
	//node1->right = node4;

	//node2->left = node3;

	//node4->left = node5;
	//node4->right=node6;


	node1->left = node2;
	node1->right = node3;

	node2->left = node4;

	//node4->left = node5;
	node3->right = node5;

	return node1;
}

void PreOrder(BTNode* root)
{
	if (root==NULL)
	{
		printf("NULL ");
		return;
	}
	//root,left,right
	printf("%d ",root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

//分治法求节点的个数
int TreeSize(BTNode* root)
{
	if (root==NULL)
	{
		return 0;
	}
	else
	{
		return TreeSize(root->left) 
			+ TreeSize(root->right)
			+1;
	}
}

int TreeHeight(BTNode* root)
{
	if (root==NULL)
	{
		return 0;
	}
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);
	return leftHeight > rightHeight ?
		leftHeight + 1 :
		rightHeight + 1;
}

int TreeLevel(BTNode* root,int k)
{
	if (root==NULL)
	{
		return 0;
	}

	if (k==1)
	{
		return 1;
	}

	return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}

//查找元素
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root==NULL)
	{
		return NULL;
	}
	if (root->data==x)
	{
		return root;
	}
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
	{
		return lret;
	}
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
	{
		return rret;
	}
	return NULL;
}

//分层遍历
void LevelOrder(BTNode* root)
{
	Quene q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q,root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->data);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}

	QueueDestroy(&q);
}

//判断是不是完全二叉树
bool TreeComplete(BTNode* root)
{
	Quene q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front==NULL)
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}
int main()
{
	BTNode* root = CreatTree();
	PreOrder(root);
	printf("\n");

	InOrder(root);
	printf("\n");

	PostOrder(root);
	printf("\n");

	printf("%d",TreeSize(root));
	printf("\n");

	printf("%d ", TreeHeight(root));
	printf("\n");

	printf("%d ", TreeLevel(root,3));
	printf("\n");

	printf("%p ", TreeFind(root, 5));
	printf("\n");

	printf("%p ", TreeFind(root, 60));
	printf("\n");

	LevelOrder(root);

	printf("TreeComplete: %d", TreeComplete(root));
	//二维数组

	return 0;
}

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"

void QueueInit(Quene* pq)
{
	assert(pq);

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueueDestroy(Quene* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while(cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueuePush(Quene* pq, QDataType x)
{
	assert(pq);

	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode==NULL)
	{
		perror("malloc fail");
		return;
	}

	newnode->next = NULL;
	newnode->data = x;

	//需要判断队列中是否有元素
	if (pq->head==NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

	pq->size++;
}

void QueuePop(Quene* pq)
{
	assert(pq);//确保有队列
	assert(pq->head != NULL);//确保队列不为空

	if (pq->head->next==NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}

int QueueSize(Quene* pq)
{
	assert(pq);

	return pq->size;
}

bool QueueEmpty(Quene* pq)
{
	assert(pq);

	return pq->size==0;
}

QDataType QueueFront(Quene* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}

QDataType QueueBack(Quene* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

Queue.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

typedef struct BinaryTreeNode* QDataType;

//单个节点
typedef struct QueneNode
{
	struct QueneNode* next;
	QDataType data;
}QNode;

//整个队列
typedef struct Quene
{
	QNode* head;
	QNode* tail;
	int size;
}Quene;

//初始化
void QueueInit(Quene* pq);
//销毁
void QueueDestroy(Quene* pq);


//入队
void QueuePush(Quene* pq, QDataType x);
//出队
void QueuePop(Quene* pq);

//计算队列中元素的个数
int QueueSize(Quene* pq);
//判断队列是否为空
bool QueueEmpty(Quene* pq);

//队列中的队头元素
QDataType QueueFront(Quene* pq);
//队列中的队尾元素
QDataType QueueBack(Quene* pq);

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/825057.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL数据库服务器安装与配置（步骤简单详细，看完可学会下载MySQL所有版本）

MySQL数据库服务器安装与配置（步骤简单详细，看完可学会下载MySQL所有版本）

目录 引言 一&#xff0c;5.6.51数据库服务器下载 二&#xff0c;8.1.0最新版数据库服务器下载 三&#xff0c;MySQL客户端下载 引言 个人认为MySQl数据库目前推荐的两个版本系列为5.6.51和8.系列。 至于我们为什么要下载两个版本呢&#xff1f;是因为官方在数据库下载的结构…
阅读更多...
C++：STL的引入和string类

C++：STL的引入和string类

文章目录 STLSTL是什么STL的六大组件 stringstring类内成员函数迭代器 STL STL是什么 什么是STL&#xff1f;STL是C标准库的重要组成部分&#xff0c;不仅是一个可复用的组件库&#xff0c;而且是一个包罗数据结构与算法的软件框架。 STL的六大组件 要学一个新知识&#xf…
阅读更多...
微信小程序 - scroll-view组件之上拉加载下拉刷新（解决上拉加载不触发）

微信小程序 - scroll-view组件之上拉加载下拉刷新（解决上拉加载不触发）

前言 最近在做微信小程序项目中&#xff0c;有一个功能就是做一个商品列表分页限流然后实现上拉加载下拉刷新功能&#xff0c;遇到了一个使用scroll-viwe组件下拉刷新事件始终不触发问题&#xff0c;网上很多说给scroll-view设置一个高度啥的就可以解决&#xff0c;有些人设置了…
阅读更多...
嵌入式软件开发有没有捷径

嵌入式软件开发有没有捷径

嵌入式软件开发有没有什么捷径&#xff1f;不定期会收到类似的问题&#xff0c;我只想说&#xff1a;嵌入式软件开发没有捷径 说实话&#xff0c;有这种想法的人&#xff0c;我其实想劝你放弃。对于绝大多数普通人&#xff0c;一步一个脚印就是捷径。 当然&#xff0c;这个问题…
阅读更多...
若依（RuoYi）系统添加自定义的模块

若依（RuoYi）系统添加自定义的模块

RuoYi系统是干什么用的，这里不过多说明了，自己搜一下，其提供的功能己经基本满足了一些简单的系统应用，如果想进行二次开发的小伙伴，可能会想仅仅用Ruoyi的后台权限管理，但是业务功能想进行自定义，可以借鉴一下本文。我们用的是前后端分离版 一、前端的自定义模块 其实在…
阅读更多...
Drools用户手册翻译——第四章 Drools规则引擎（九）Phreak算法

Drools用户手册翻译——第四章 Drools规则引擎（九）Phreak算法

这个地方我是先了解了Rete算法&#xff0c;才来看得这一部分&#xff0c;结果发现好像没有什么用......完全不知道讲的什么&#xff0c;估计之后在用的时候慢慢会明白。 RETE算法笔记&#xff1a;http://t.csdn.cn/iNZ8V 甩锅声明&#xff1a;本人英语一般&#xff0c;翻译只…
阅读更多...
二叉树的最近公共祖先,二叉搜索树的最近公共祖先（同一个思路）

二叉树的最近公共祖先,二叉搜索树的最近公共祖先（同一个思路）

题目链接   二叉树的最近公共祖先   给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。   百度百科中最近公共祖先的定义为&#xff1a;“对于有根树 T 的两个节点 p、q&#xff0c;最近公共祖先表示为一个节点 x&#xff0c;满足 x 是 p、q 的祖先且 x 的深度尽可…
阅读更多...
GD32F103输入捕获

GD32F103输入捕获

GD32F103输入捕获程序&#xff0c;经过多次测试&#xff0c;终于完成了。本程序将TIMER2_CH2通道映射到PB0引脚&#xff0c;捕获PB0引脚低电平脉冲时间宽度。PB0是一个按钮&#xff0c;第1次按下采集一个值保存到TIMER2_CountValue1中&#xff0c;第2次按下采集一个值保存到TIM…
阅读更多...
如何使jwt生成的 token在用户登出之后失效?

如何使jwt生成的 token在用户登出之后失效?

问题1:如何使jwt生成的 token在用户登出之后失效? 由于jwt生成的token是无状态的,这体现在我们在每一次请求时 request都会新建一个session对象: 举个例子: @PostMapping(value = "/authentication/logout") public ResponseEntity<BaseResult> logOut(Htt…
阅读更多...
第十次CCF计算机软件能力认证

第十次CCF计算机软件能力认证

第一题&#xff1a;分蛋糕 小明今天生日&#xff0c;他有 n 块蛋糕要分给朋友们吃&#xff0c;这 n 块蛋糕&#xff08;编号为 1 到 n&#xff09;的重量分别为 a1,a2,…,an。 小明想分给每个朋友至少重量为 k 的蛋糕。 小明的朋友们已经排好队准备领蛋糕&#xff0c;对于每个朋…
阅读更多...
Spring之浅谈AOP技术

Spring之浅谈AOP技术

前言 AOP&#xff1a;Aspect Oriented Programming&#xff08;面向切面编程&#xff09;&#xff0c;一种编程范式&#xff0c;指导开发者如何组织程序结构。 OOP&#xff08;Object Oriented Programming&#xff09;面向对象编程 AOP和OOP一样都是一种编程思想&#xff0c…
阅读更多...
佑友防火墙后台命令执行漏洞

佑友防火墙后台命令执行漏洞

漏洞描述 佑友防火墙 后台维护工具存在命令执行&#xff0c;由于没有过滤危险字符&#xff0c;导致可以执行任意命令 漏洞复现 访问url 使用弱口令登录佑友防火墙后台 User: admin Pass: hicomadmin 点击系统管理 维护工具 Ping 输入可执行命令 127.0.0.1|cat /etc/passwd
阅读更多...
【高级程序设计语言C++】AVL树

【高级程序设计语言C++】AVL树

1. AVL树的概念2. AVL树的旋转2.1. 左单旋2.2 右单旋2.3 左右双旋2.4 右左双旋 1. AVL树的概念 AVL树是一种自平衡二叉搜索树&#xff0c;它在每次插入或删除节点时自动调整以保持树的平衡。AVL树的平衡是通过节点的高度差来衡量的&#xff0c;即左子树的高度和右子树的高度之…
阅读更多...
Gartner：2022年全球IaaS公有云服务市场增长30%，首次突破1000亿美元

Gartner：2022年全球IaaS公有云服务市场增长30%，首次突破1000亿美元

根据Gartner的统计结果&#xff0c;2022年全球基础设施即服务&#xff08;IaaS&#xff09;市场从2021年的928亿美元增长到1203亿美元&#xff0c;同比增长29.7%。亚马逊在2022年继续排在IaaS市场的第一名&#xff0c;其次是微软、阿里巴巴、谷歌和华为。 最新消息&#xff0c;…
阅读更多...
Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建 qt

Spring Cloud+Spring Boot+Mybatis+uniapp+前后端分离实现知识付费平台免费搭建 qt

&#xfeff;Java版知识付费源码 Spring CloudSpring BootMybatisuniapp前后端分离实现知识付费平台 提供职业教育、企业培训、知识付费系统搭建服务。系统功能包含&#xff1a;录播课、直播课、题库、营销、公司组织架构、员工入职培训等。 提供私有化部署&#xff0c;免费售…
阅读更多...
无涯教程-Lua - 文件I/O

无涯教程-Lua - 文件I/O

I/O库用于在Lua中读取和处理文件。 Lua中有两种文件操作&#xff0c;即隐式(Implicit)和显式(Explicit)操作。 对于以下示例&#xff0c;无涯教程将使用例文件test.lua&#xff0c;如下所示。 -- sample test.lua -- sample2 test.lua 一个简单的文件打开操作使用以下语句。…
阅读更多...
计算机毕设 深度学习猫狗分类 - python opencv cnn

计算机毕设 深度学习猫狗分类 - python opencv cnn

文章目录 0 前言1 课题背景2 使用CNN进行猫狗分类3 数据集处理4 神经网络的编写5 Tensorflow计算图的构建6 模型的训练和测试7 预测效果8 最后 0 前言 &#x1f525; 这两年开始毕业设计和毕业答辩的要求和难度不断提升&#xff0c;传统的毕设题目缺少创新和亮点&#xff0c;往…
阅读更多...
vscode 第一个文件夹在上一层文件夹同行,怎么处理

vscode 第一个文件夹在上一层文件夹同行,怎么处理

我的是这样的 打开终端特别麻烦 解决方法就是 打开vscode里边的首选项 进入设置 把Compact Folders下边对勾给勾掉
阅读更多...
acwing 1064 小国王 线性状态压缩DP

acwing 1064 小国王 线性状态压缩DP

输入 3 2输出 16&#x1f37a; AC code #include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<vector>using namespace std;typedef long long ll; const int N 12; const int M 1 << 10, K 110;//…
阅读更多...
2.如何运用python成为顶级黑客

2.如何运用python成为顶级黑客

阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023