题目链接
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
实例1:

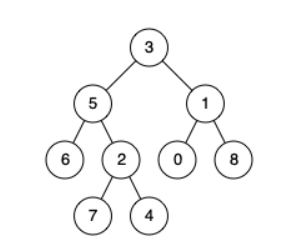
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
实例2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身
解题思路
给出一颗二叉树,再给出两个节点,p和q,且都在这颗二叉树中。
分三种情况
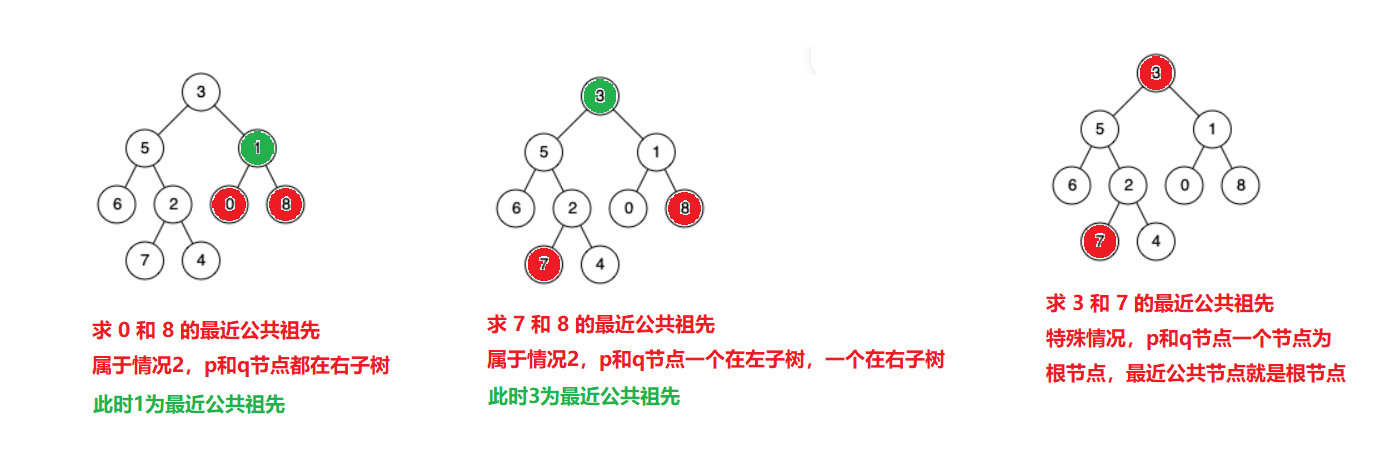
情况1:p节点和q节点都在左子树,此时最近公共祖先也在左子树
情况2:p节点和q节点都在右子树,此时最近公共祖先也在右子树
情况3:p节点和q节点一个在左子树,一个在右子树,此时这颗树的根就是最近公共节点
特殊情况:如果p节点或者q节点其中一个为根节点,此时最近公共祖先就是根节点
采用递归,分解子问题

解题的本质思路就是递归调用解决子问题,将原问题划分为子问题
class Solution {
public:
bool Find(TreeNode* root, TreeNode* val)
{
if (root == NULL)return false;
return root == val || Find(root->left, val) || Find(root->right, val);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//判断特殊情况,根节点为空
if (root == NULL)return NULL;
//特殊情况,p节点或者q节点其中一个为根节点,此时最近公共祖先就是根节点
if (root == p || root == q)return root;
//用来判断p和q在左右子树位置的变量
bool pInLeft, pInRight, qInLeft, qInRight;
pInLeft = Find(root->left, p);
pInRight = !pInLeft;
qInLeft = Find(root->left, q);
qInRight = !qInLeft;
if(pInLeft && qInLeft)
{
//情况1:p和q都在左子树,递归调用根节点的左子树
return lowestCommonAncestor(root->left,p,q);
}else if(pInRight&& qInRight)
{
//情况2:p和q都在右子树,递归调用根节点的右子树
return lowestCommonAncestor(root->right,p,q);
}else{
//p和q,一个在左子树,一个在右子树,此时根节点为最近公共祖先
return root;
}
}
};
题目链接
二叉树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
实例1:
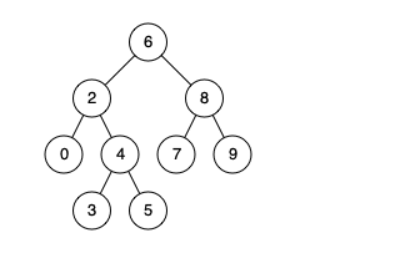
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
实例2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
思路同上,不过二叉树的最近公共祖先需要先寻找p和q的位置进行递归调用,
由于二叉搜索树的特殊,我们不需要再手动查找p和q的位置,只需进行判断大小即可,二叉搜索树的性质,根节点的左子树元素比根节点小,根节点的左子树元素比根节点大。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL)return NULL;
if(p==root||q==root)return root;
if(p->val>root->val&&q->val>root->val)
{
//都在右子树
return lowestCommonAncestor(root->right,p,q);
}else if(p->val<root->val&&q->val<root->val)
{
//都在左子树
return lowestCommonAncestor(root->left,p,q);
}else{
//一个在左,一个在右
return root;
}
}
};