1. AVL树的概念

AVL树是一种自平衡二叉搜索树，它在每次插入或删除节点时自动调整以保持树的平衡。AVL树的平衡是通过节点的高度差来衡量的，即左子树的高度和右子树的高度之差不超过1。

AVL树的特点如下：

• 每个节点都有一个平衡因子，定义为左子树的高度减去右子树的高度。平衡因子的值只能是-1、0或1。
• AVL树中的任何节点的左子树和右子树都是AVL树。
• 对于AVL树中的每个节点，左子树的高度和右子树的高度之差不超过1。

当向AVL树中插入新节点或删除节点时，AVL树会根据节点的平衡因子进行自动调整。如果插入或删除导致某个节点的平衡因子超过了允许的范围（-1、0或1），则需要通过旋转操作来重新平衡树。

2. AVL树的旋转

AVL树的旋转操作包括左旋和右旋。左旋是指将一个节点的右子树提升为其父节点，并将父节点降为其左子节点。右旋是指将一个节点的左子树提升为其父节点，并将父节点降为其右子节点。通过旋转操作，AVL树可以保持平衡。

2.1. 左单旋

左单旋的情况简图如下：

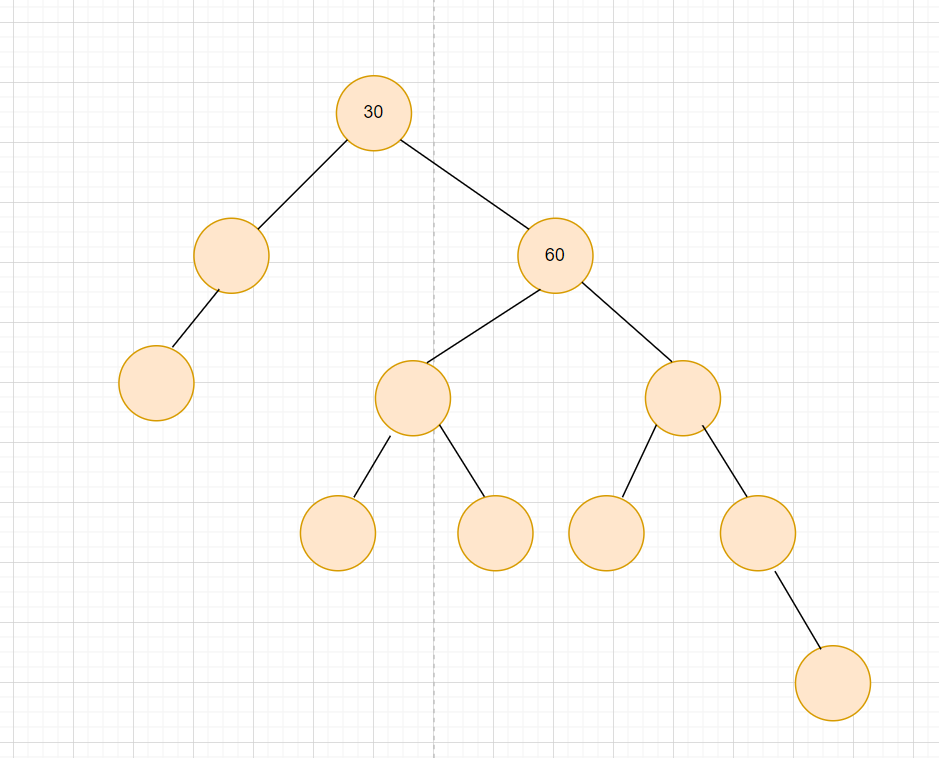
需要左单旋，那么就是右边的分支出现了平衡因子异常，他的形象图类似一条直线。

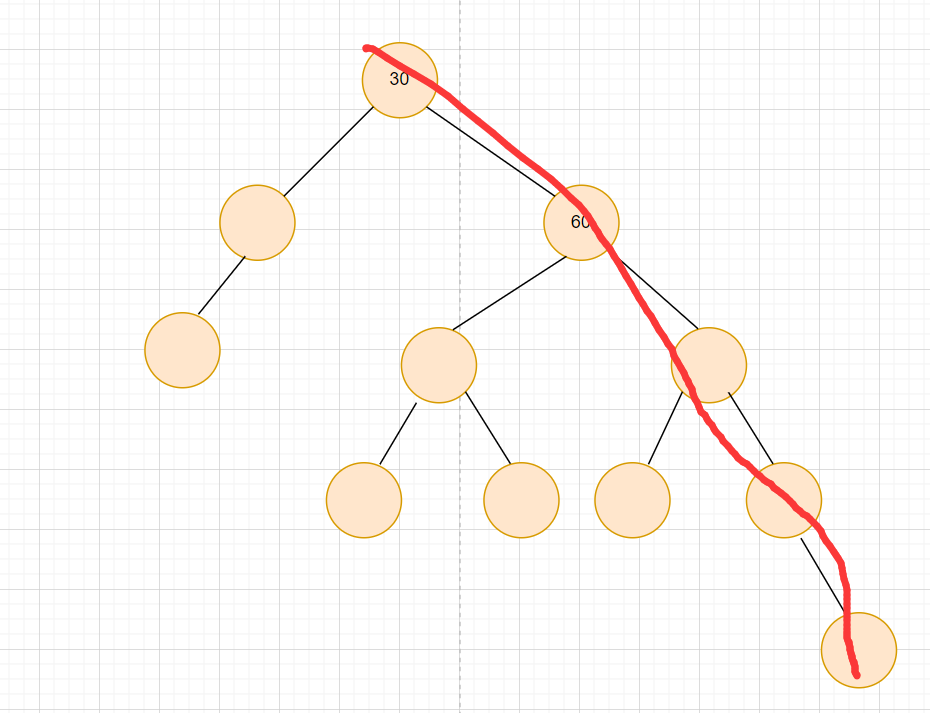
总体来说就是右边高，需要向左旋转，依据的是平衡因子来确定是否需要旋转。

当父亲的平衡因子为2，子树的平衡因子为1的时候，就需要左单旋。旋转完成后，需要注意平衡因子的更新。

// 左单旋
void RotateL(Node* pParent)
{
    Node* subR = pParent->_pRight;
    Node* subRL = subR->_pLeft;

    pParent->_pRight = subRL;
    if (subRL)
    {
        subRL->_pParent = pParent;
    }

    Node* pPParent = pParent->_pParent;
    subR->_pLeft = pParent;
    pParent->_pParent = subR;
    if (pPParent)
    {
        if (pParent == pPParent->_pLeft)
        {
            pPParent->_pLeft = subR;
        }
        else if (pParent == pPParent->_pRight)
        {
            pPParent->_pRight = subR;
        }
        subR->_pParent = pPParent;
    }
    else
    {
        _root = subR;
        _root->_pParent = nullptr;
    }
    subR->_bf = pParent->_bf = 0;
}

旋转之后的树状图如下：

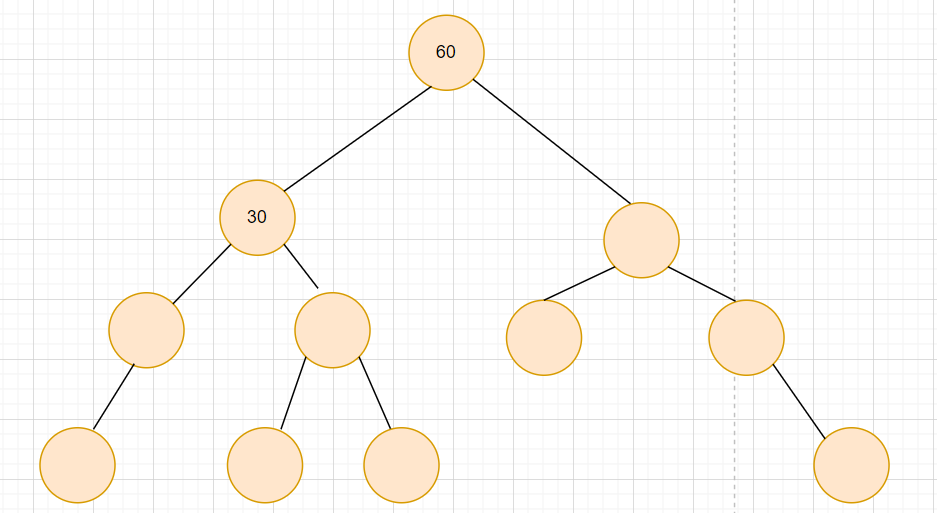
2.2 右单旋

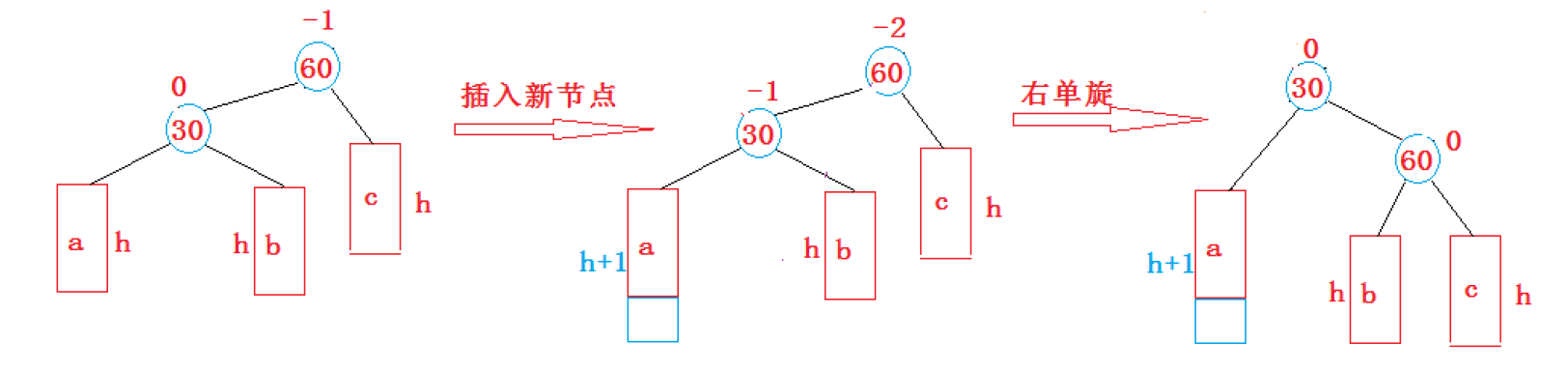
具体的图像请读者自行画出。

总体来说就是，左边高，就需要往右边旋转，依据平衡因子来决定。

当父亲的平衡因子为-2，子树的平衡因子为-1时就需要右单旋。旋转完成后需要注意平衡因子的更新。

// 右单旋
void RotateR(Node* pParent)
{
    Node* subL = pParent->_pLeft;
    Node* subLR = subL->_pRight;
    pParent->_pLeft = subLR;
    if (subLR)
    {
        subLR->_pParent = pParent;
    }
    Node* pPParent = pParent->_pParent;
    subL->_pRight = pParent;
    pParent->_pParent = subL;
    if (pPParent)
    {
        if (pPParent->_pLeft == pParent)
        {
            pPParent->_pLeft = subL;
        }
        else if (pPParent->_pRight == pParent)
        {
            pPParent->_pRight = subL;
        }
        subL->_pParent = pPParent;
    }
    else
    {
        _root = subL;
        _root->_pParent = nullptr;
    }
    pParent->_bf = subL->_bf = 0;
}

2.3 左右双旋

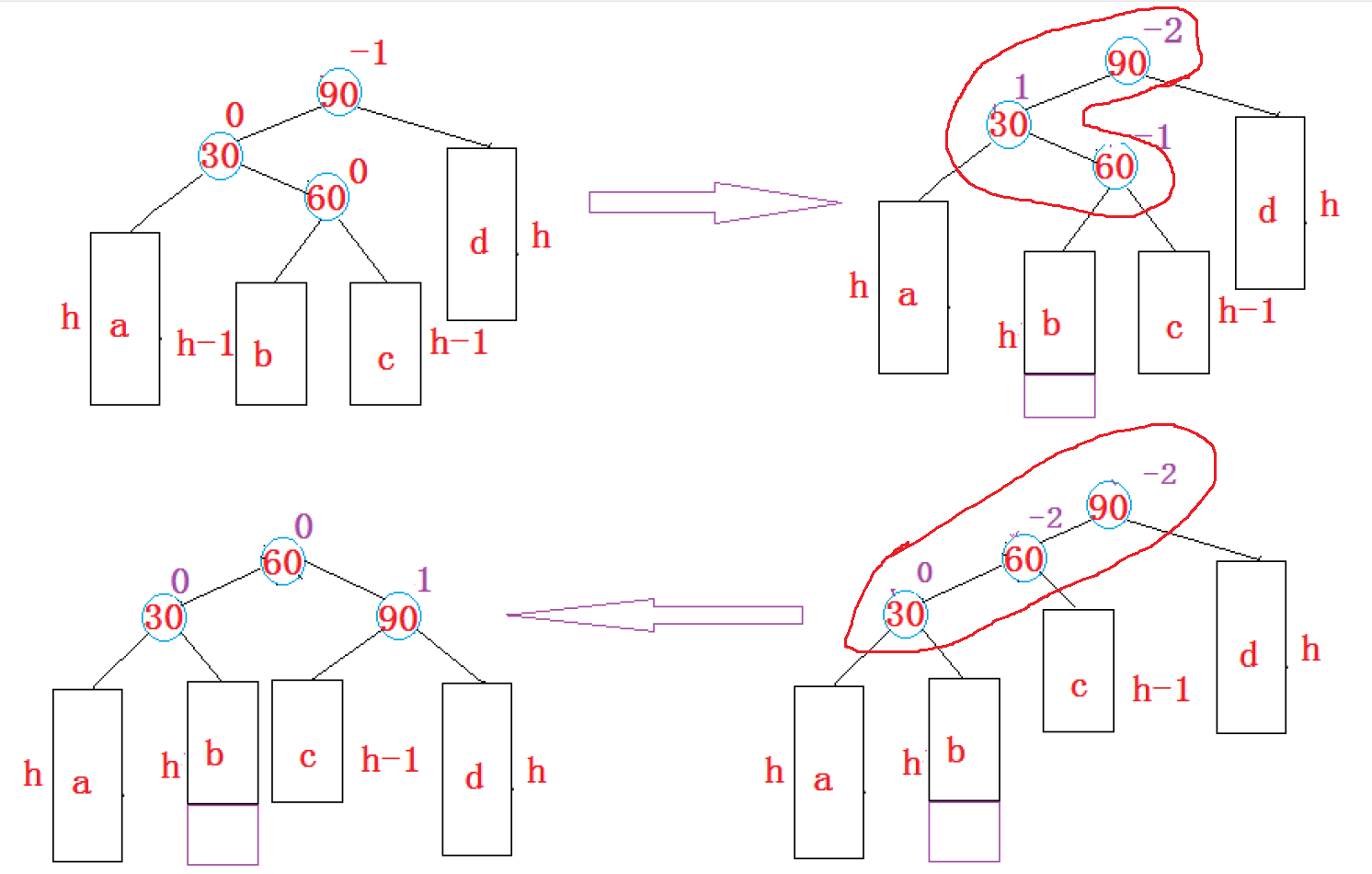
具体来说就是，先进行左单旋，捋直后进行右单旋。依据平衡因子来决定。

当父亲的平衡因子为-2，子树的平衡因子为1时，就要进行左右双旋。

void RotateLR(Node* pParent)
	{
		Node* subL = pParent->_pLeft;
		Node* subLR = subL->_pRight;
		int bf = subLR->_bf;
		RotateL(subL);
		RotateR(pParent);
		if (bf == 0)
		{
			subL->_bf = 0;
			pParent->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			subL->_bf = 0;
			pParent->_bf = 1;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			subL->_bf = -1;
			pParent->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

2.4 右左双旋

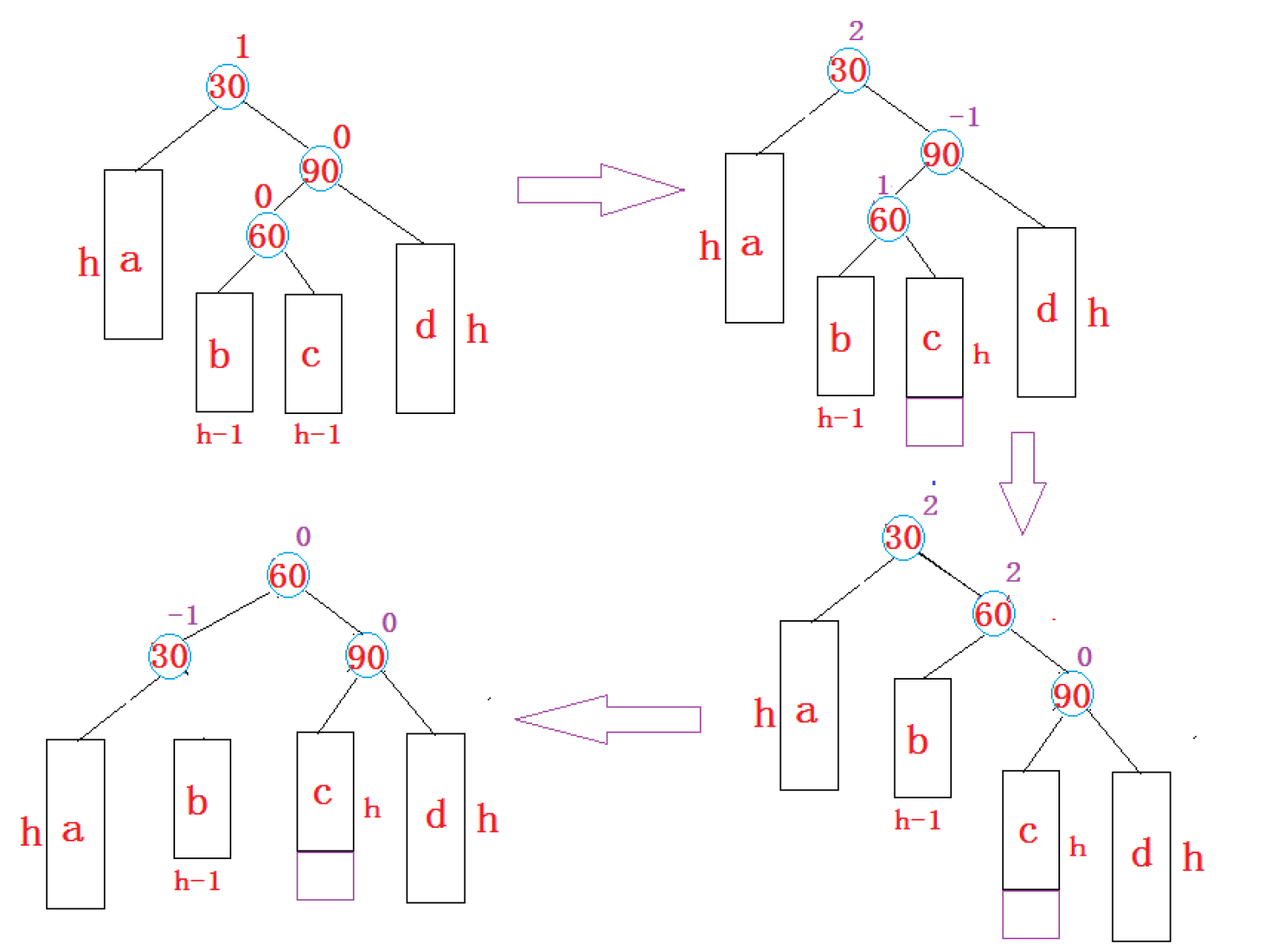
参考左右双旋，根据上图自行绘出节点的走势。

右左双旋的依据也是根据平衡因子来决定的，当父亲的平衡因子为2，子树的平衡因子为-1时，即要进行右左双旋。

// 右左双旋
void RotateRL(Node* pParent)
{
    Node* subR = pParent->_pRight;
    Node* subRL = subR->_pLeft;
    int bf = subRL->_bf;
    RotateR(subR);
    RotateL(pParent);
    if (bf == -1)
    {
        subRL->_bf = 0;
        pParent->_bf = 1;
        subR->_bf = 0;
    }
    else if (bf == 0)
    {
        subRL->_bf = 0;
        pParent->_bf = 0;
        subR->_bf = 0;
    }
    else if (bf == 1)
    {
        subRL->_bf = 0;
        pParent->_bf = -1;
        subR->_bf = 0;
    }
    else
    {
        assert(false);
    }
}