目录
- 第五章:树
- 5.1树的基本概念
- 5.1.1树的定义
- 5.1.2 基本术语
- 5.1.3 树的性质
- 5.2二叉树的概念
- 5.2.1 二叉树的定义与特性
- 5.2.2 几种特殊的二叉树
- 5.2.3 二叉树的性质
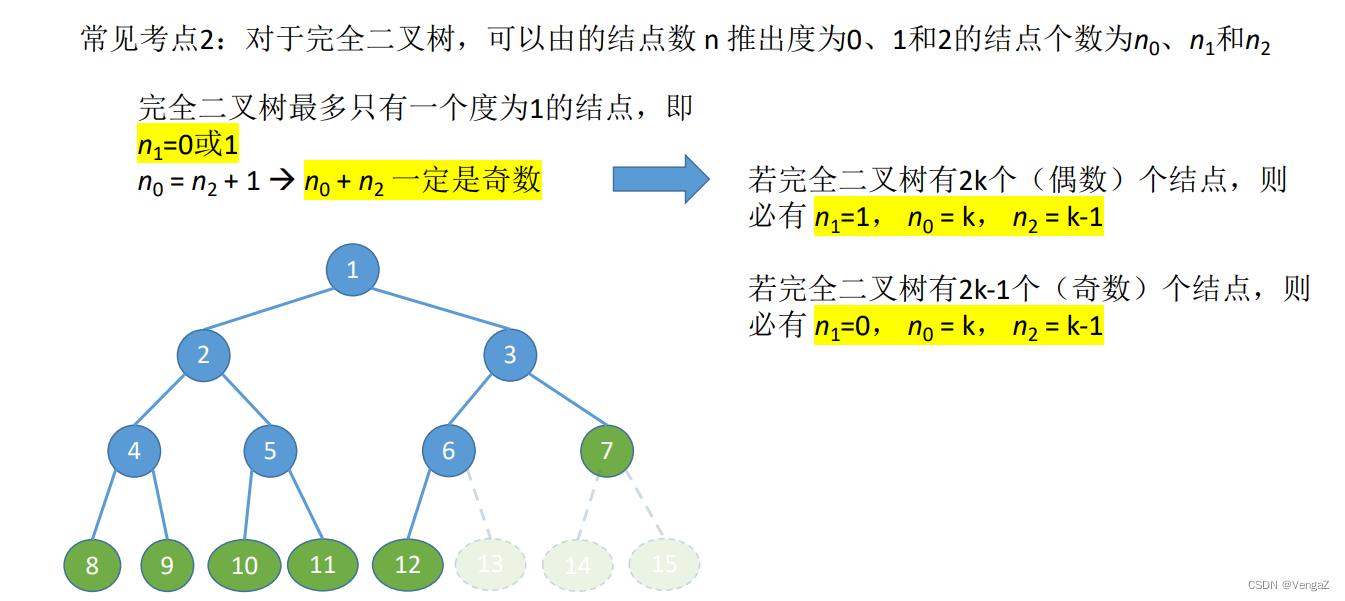
- 5.2.4 完全二叉树的性质
- 5.2.5 二叉树的存储结构
- 1. 顺序存储
- 重要的基本操作
- 非完全二叉树
- 2. 链式存储
- 逆向寻找父节点
第五章:树
5.1树的基本概念
节点数 = 度的和+1或者节点数
5.1.1树的定义

树是n个结点的有限集。
- 空树:n=0
- 根结点、分支结点、叶子结点
- 非空树的特性
- 子树
在n个结点的树中有n-1条边
5.1.2 基本术语
结点之间的关系描述
- 祖先、子孙、双亲、兄弟结点(亲兄弟同父节点、堂兄弟同一层次)
- 路径(路径只有从上往下,需要从下往上的就不存在路径)
- 路径长度(树根到每个节点的路径长度的总和)
结点、树的属性描述
- 结点的层次(深度,默认从1)——从上往下
- 结点的高度——从下往上
- 树的高度——总共多少层
- 结点的度——有几个孩子
- 树的度——各结点的度的最大值
有序树(家谱,从左到右有次序不可以互换)、无序树(左右位置没有逻辑关系,可以互换)
森林(多颗互不相交的树的集合,允许有空森林,跟树一样节点数可以为0)
森林与树的转换
- 当森林的树拥有共同根节点就是一棵树
5.1.3 树的性质
-
树中的结点数等于所有结点的度数之和加1。(这个1是根节点,因为每个节点的度代表他的直接子节点个数,这些全部相加就差根节点的个数也就是1)
-
-
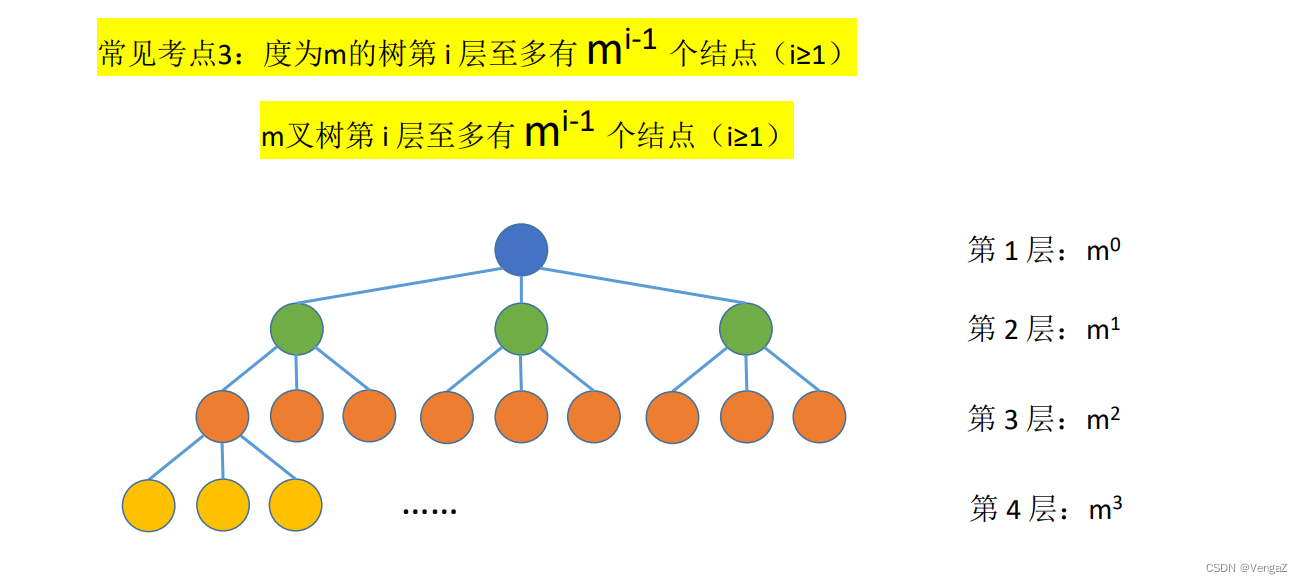
度为m的树第i层上至多有m^i-1个结点(这是因为树的度代表最多一个节点拥有的最多的子节点个数,所以至多就是指数级别的关系)
度为m的数、m叉数的区别
- m叉树,只要每个节点的孩子数小于等于m,并且不要求存在一个节点的度等于m,所以一棵二叉树也一定是一棵三叉树,四叉树·······
- 度为m的树,一定要有一个节点的度是m,所以不可能是空树,对于m叉树来说就可以是空树

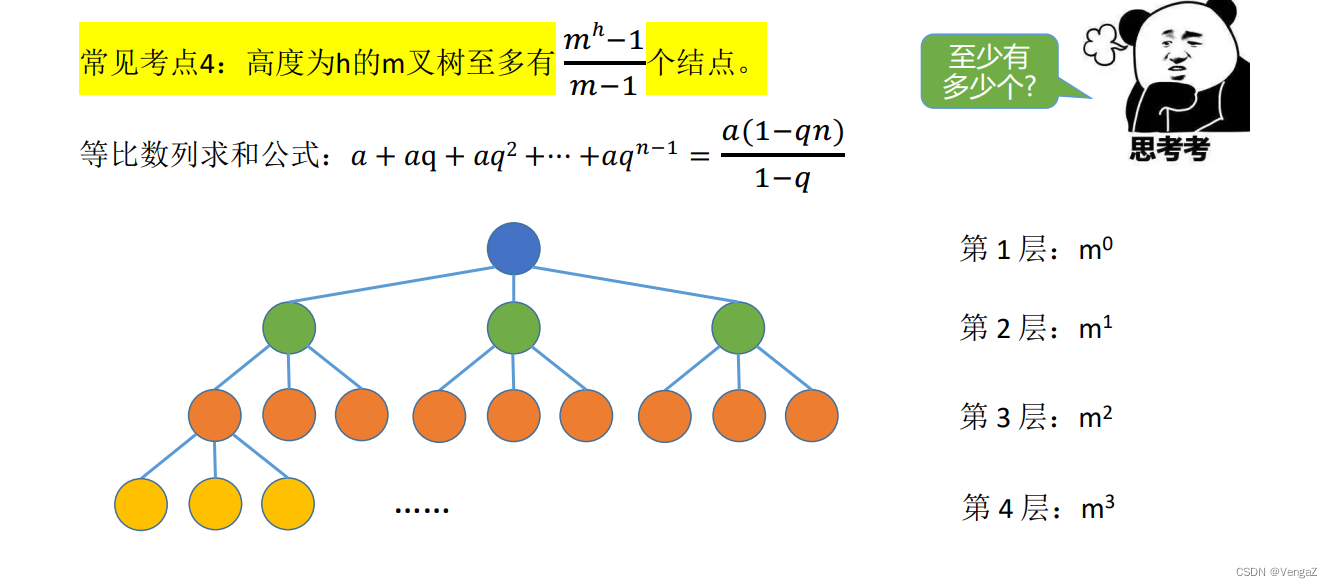
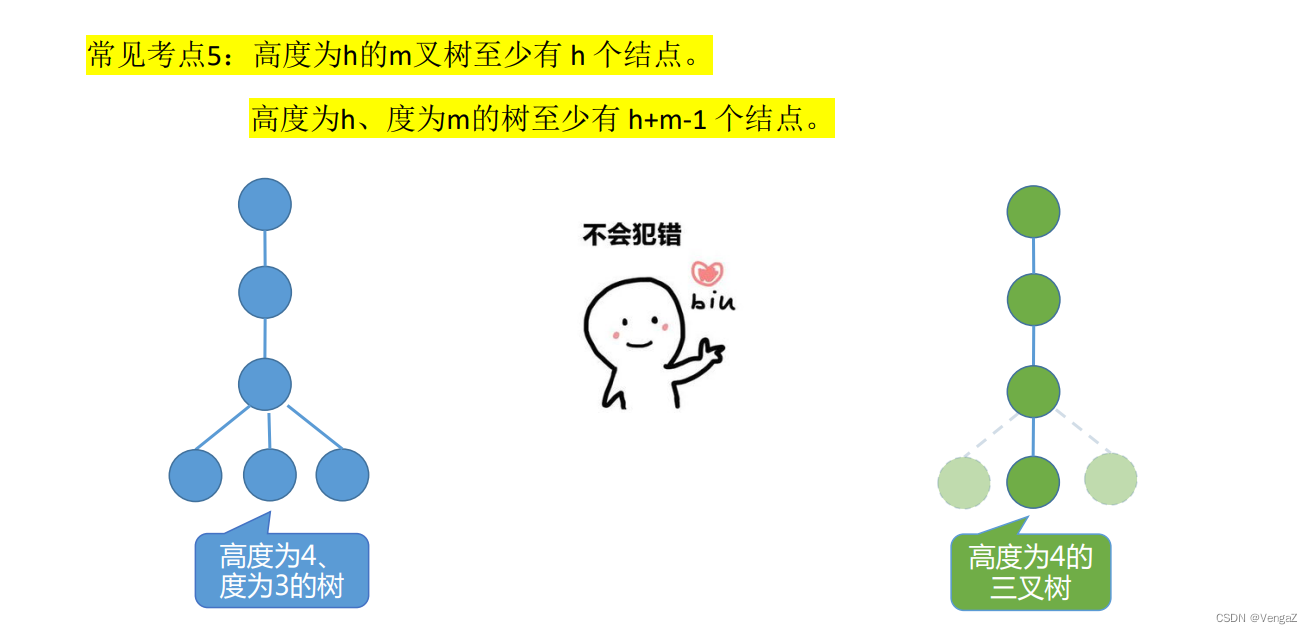
度为m,有n个节点的树:树的高度最高是,n-(m+1)+2 = n-m+1

5.2二叉树的概念
5.2.1 二叉树的定义与特性
定义:
二叉树是n(n>=0)个结点的有限集,它或者是空集(n=0),或者由一个根结点及两颗互不相交的分别称作这个根的左子树和右子树的二叉树组成。
特点:
- 每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。
- 二叉树可以是空集合,根可以有空的左子树和空的右子树。
- 二叉树有左右之分,次序不能颠倒。(有序,且子树也是二叉树)
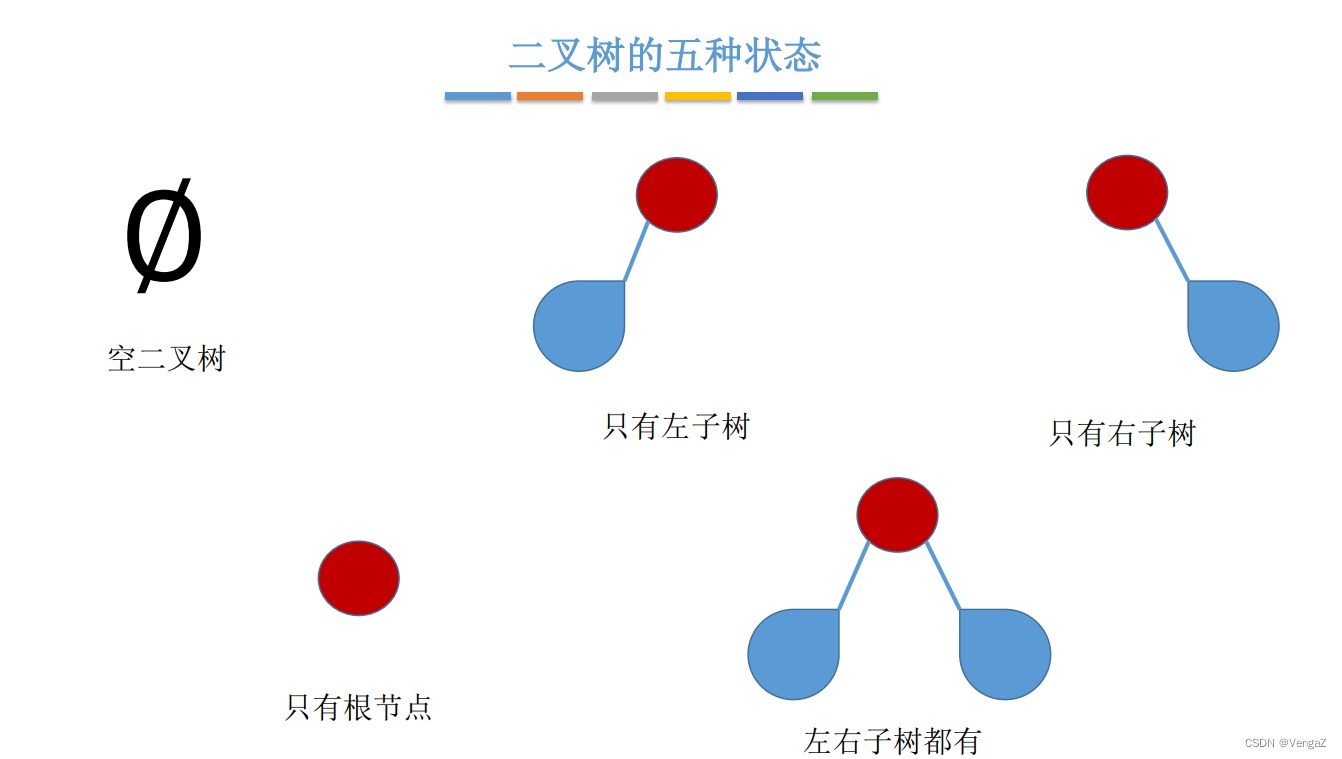
5.2.2 几种特殊的二叉树
-
满二叉树:一颗深度为k且有2^k-1个结点的二叉树称为满二叉树。每一层上的结点数都达到最大。叶子全部在最低层。
-
完全二叉树:深度为k的具有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一 一对应时,称之为完全二叉树。(缺少的只会是最后一个节点,递归这种缺少才能满足,就是不能缺少8号节点,因为这样8后边的所有节点都会变换序号,与满二叉树不一样了)
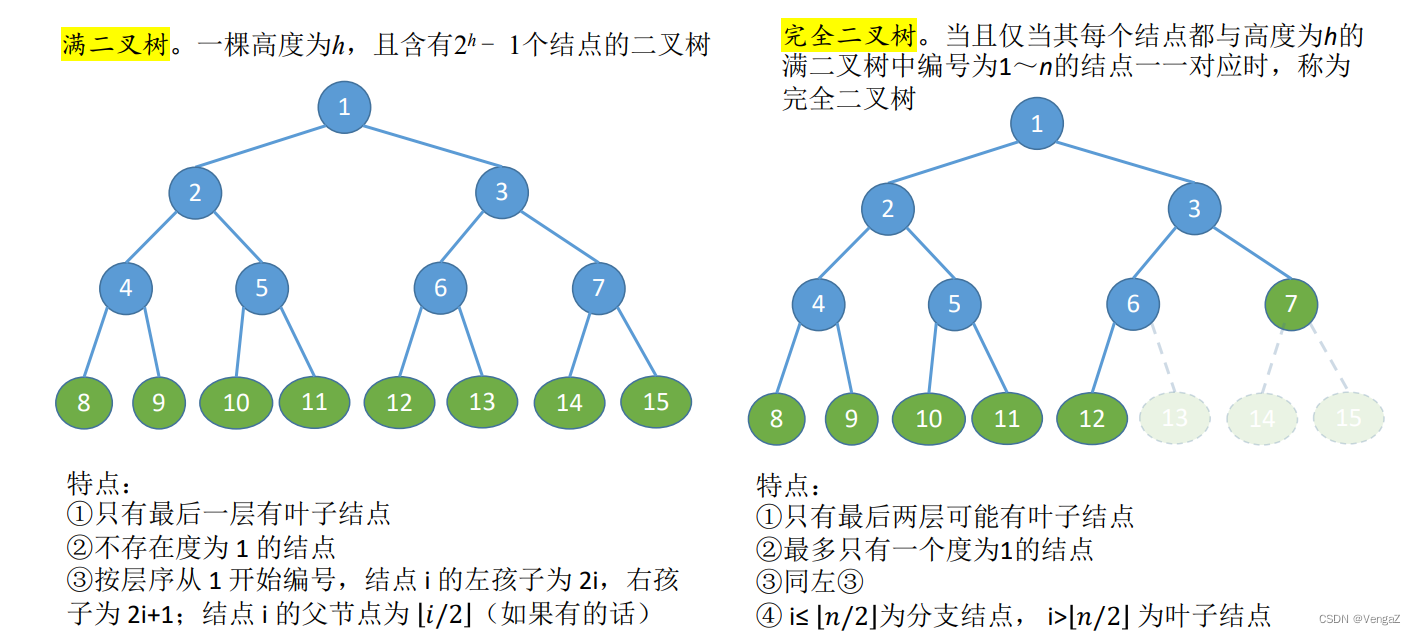
完全二叉树的最多且唯一一个度为1的节点一定有的是左孩子 -
二叉排序树
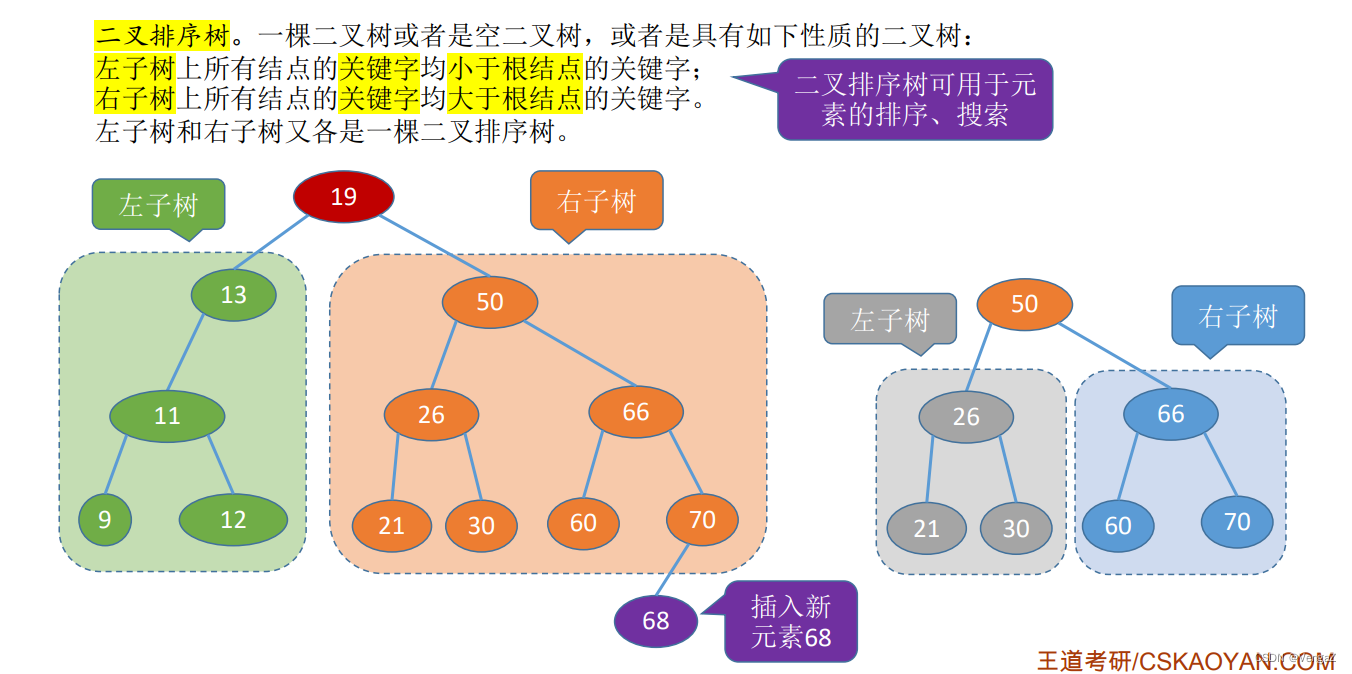
-
平衡二叉树
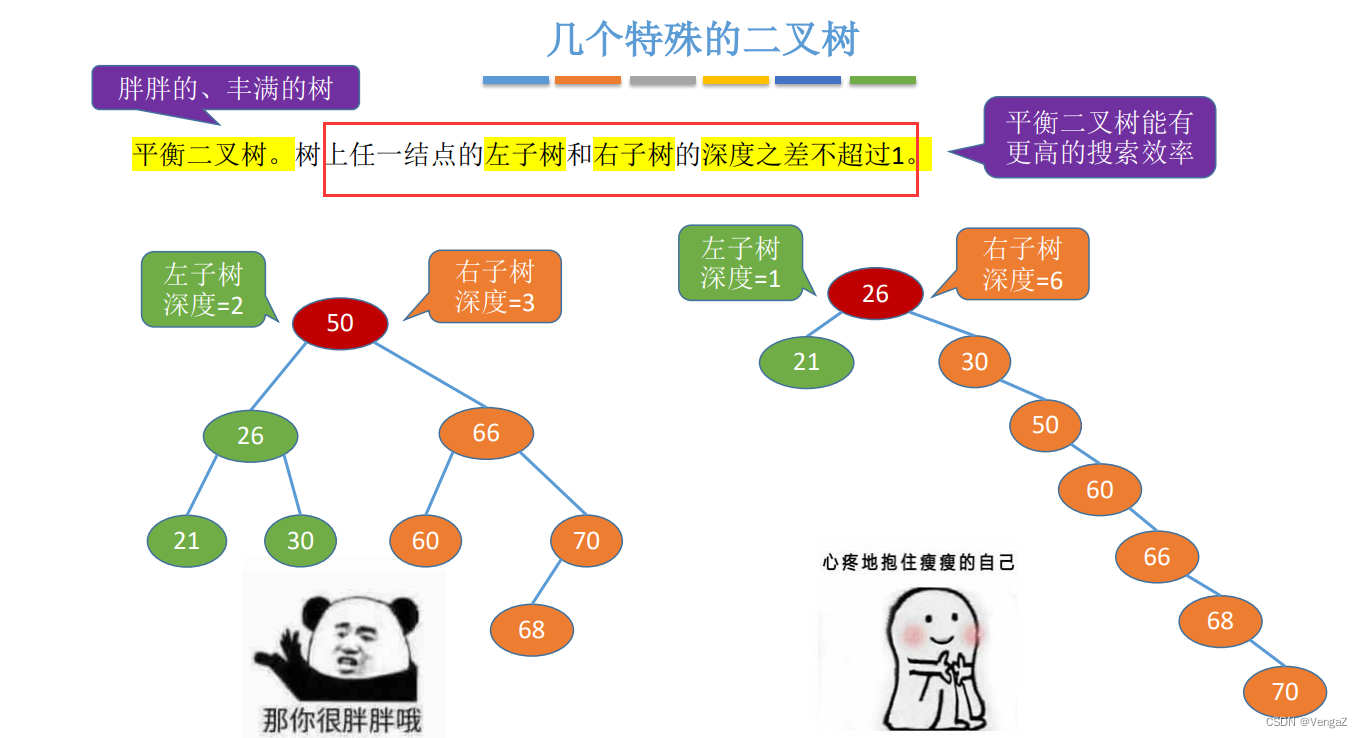
5.2.3 二叉树的性质
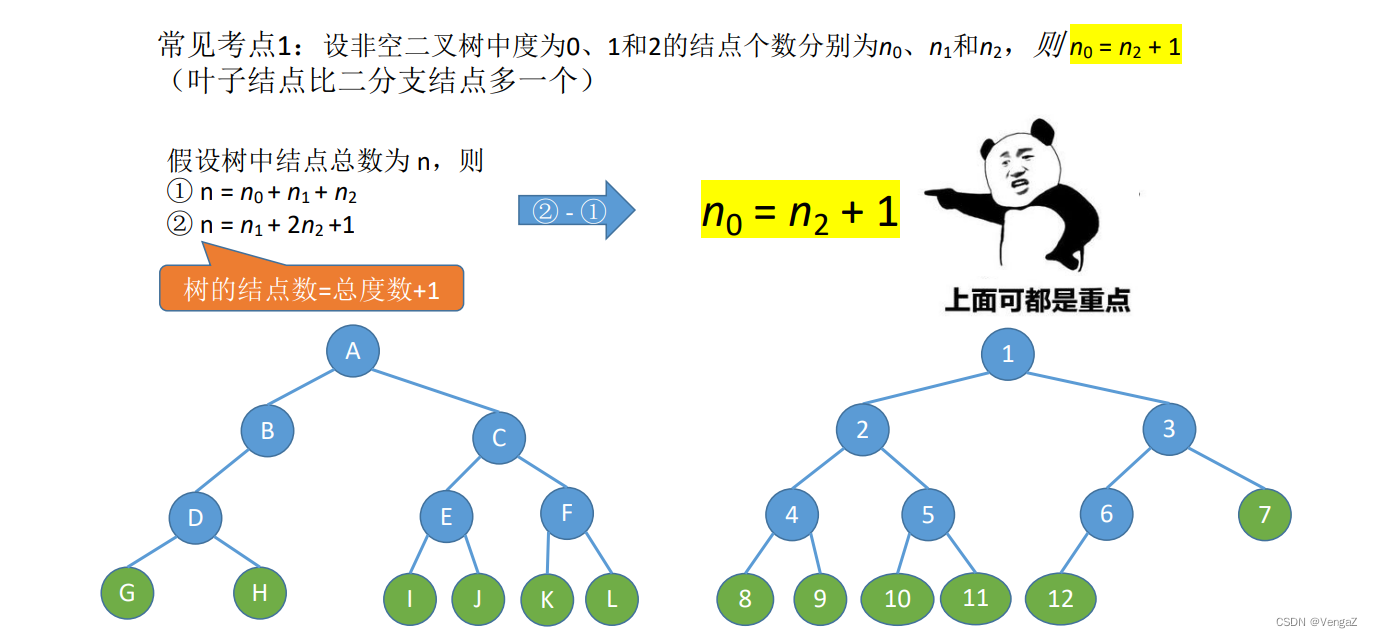
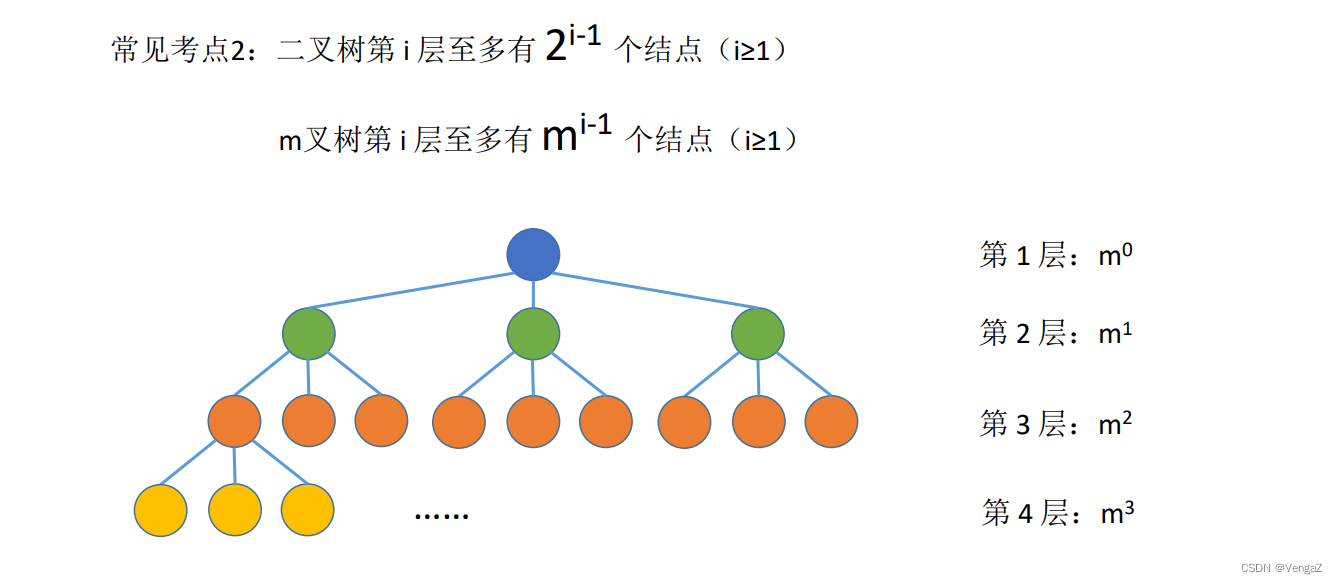
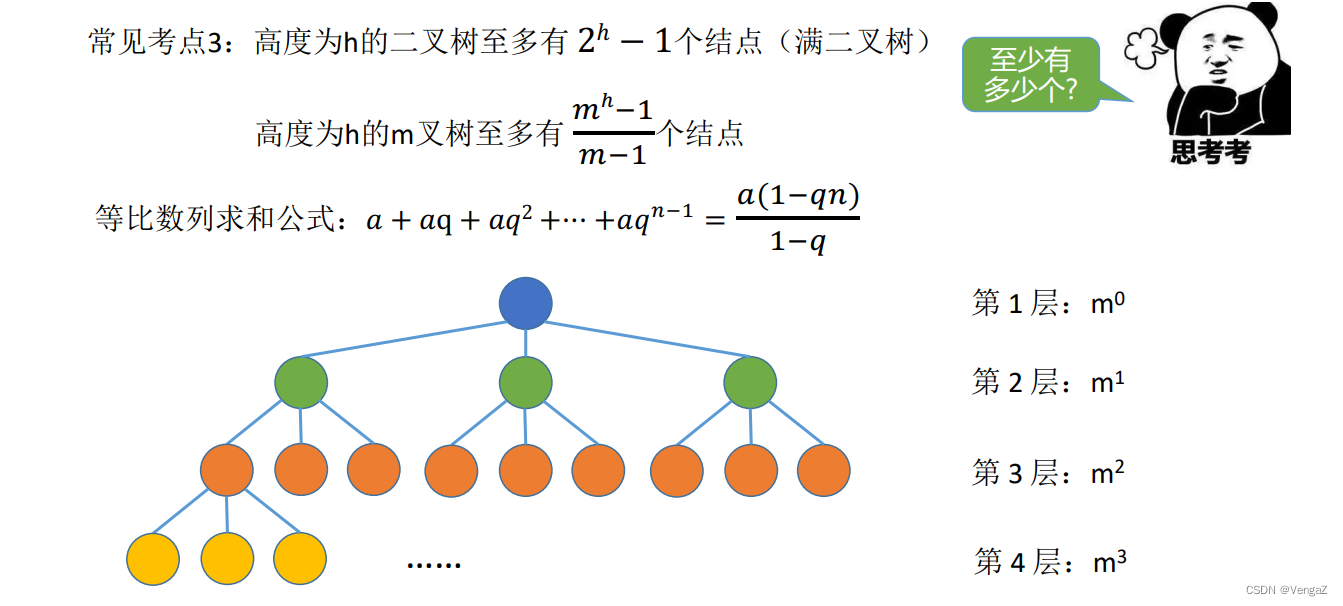
5.2.4 完全二叉树的性质
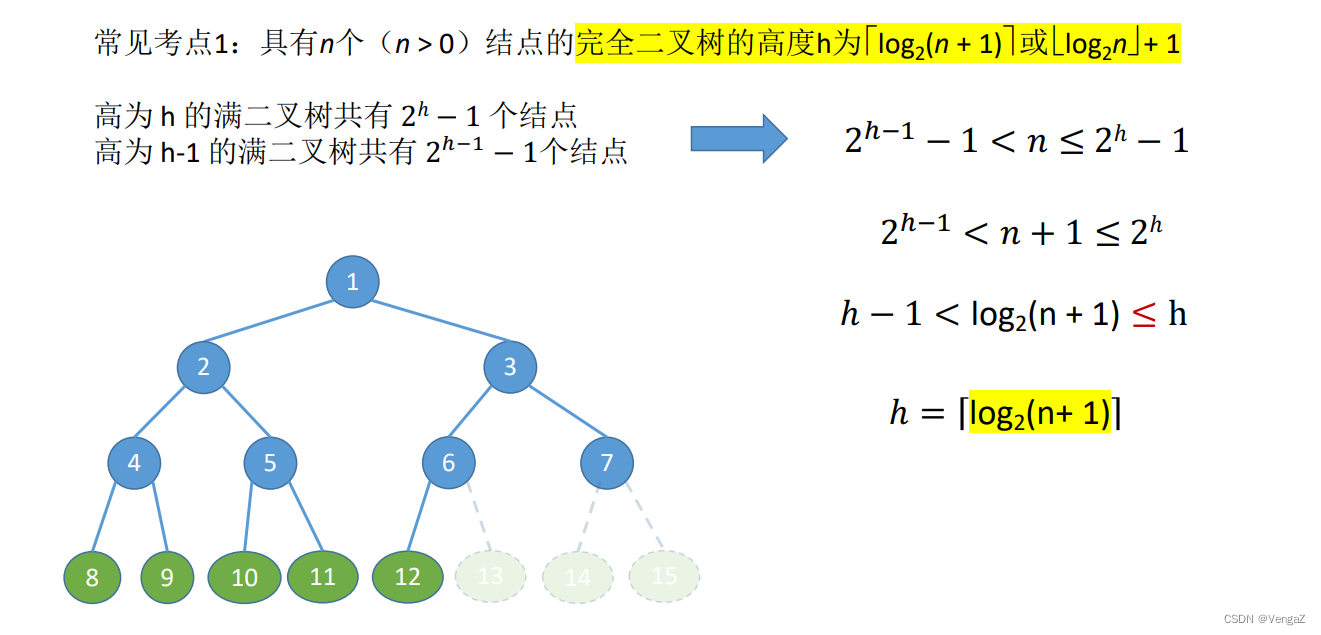

5.2.5 二叉树的存储结构
1. 顺序存储
#define MaxSize 100
struct TreeNode{
ElemType value; //结点中的数据元素
bool isEmpty; //结点是否为空
}
main(){
TreeNode t[MaxSize];
for (int i=0; i<MaxSize; i++){
t[i].isEmpty = true;
}
}
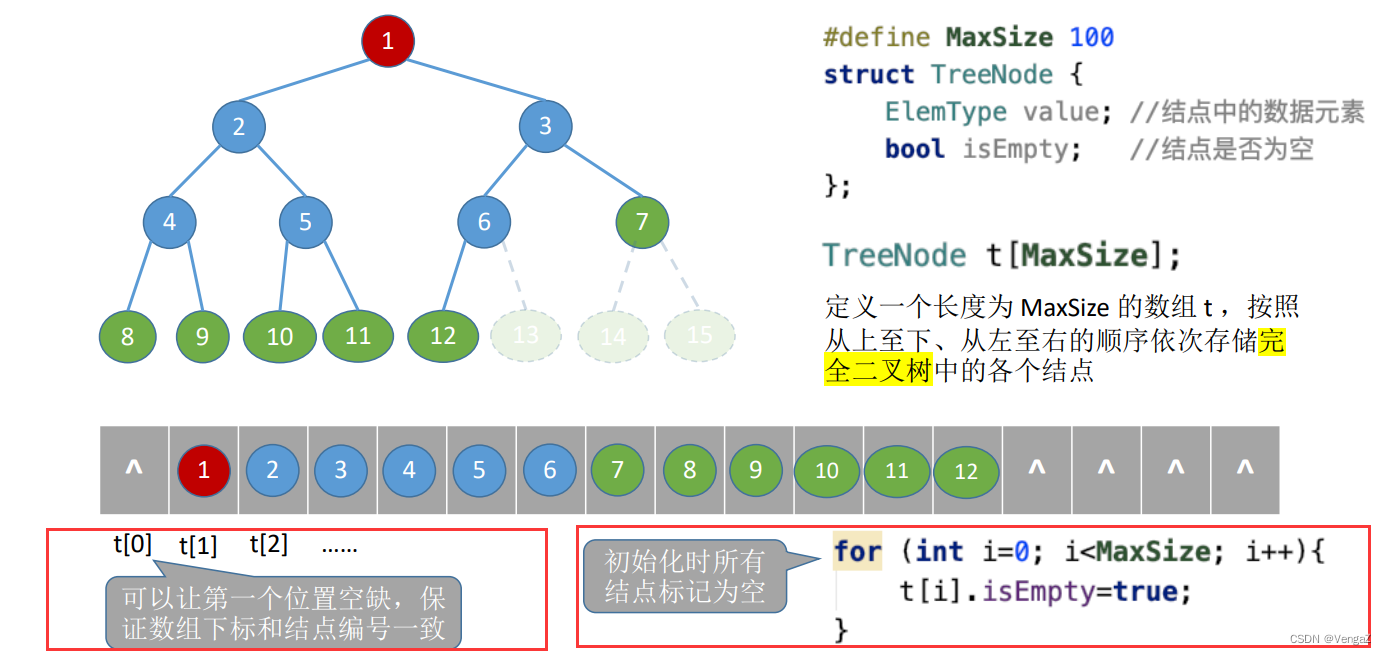
重要的基本操作

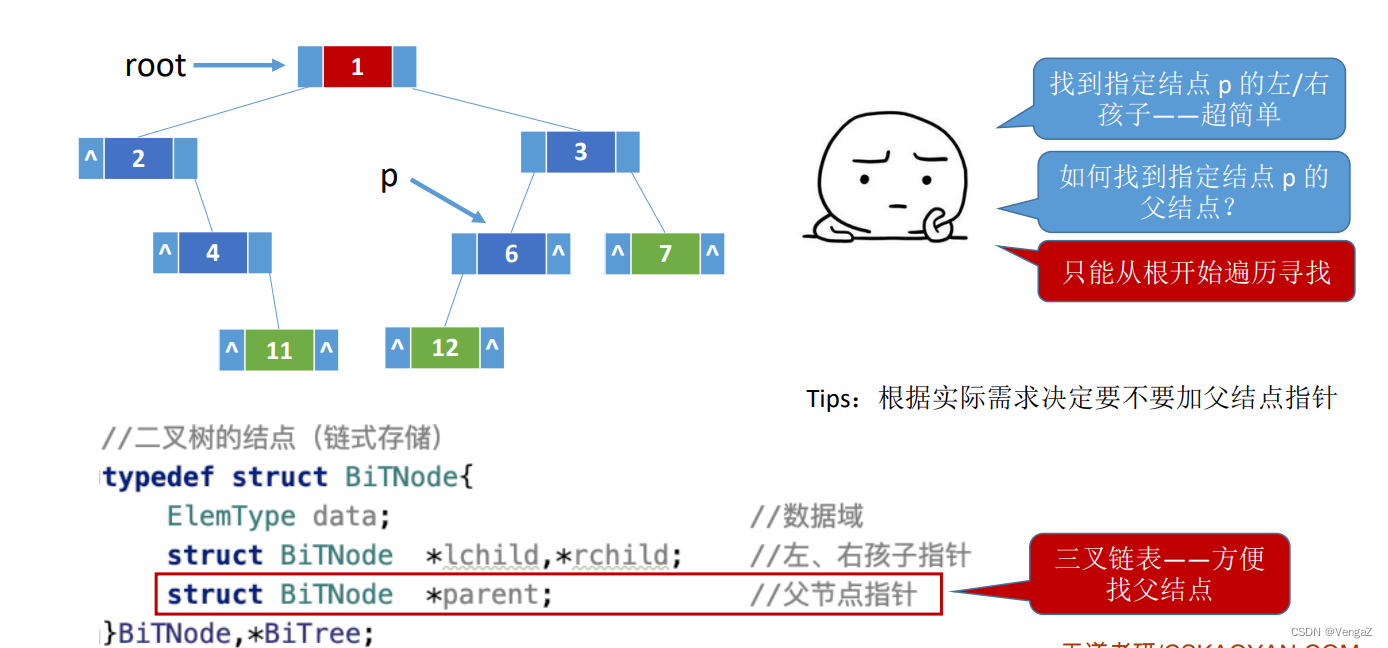
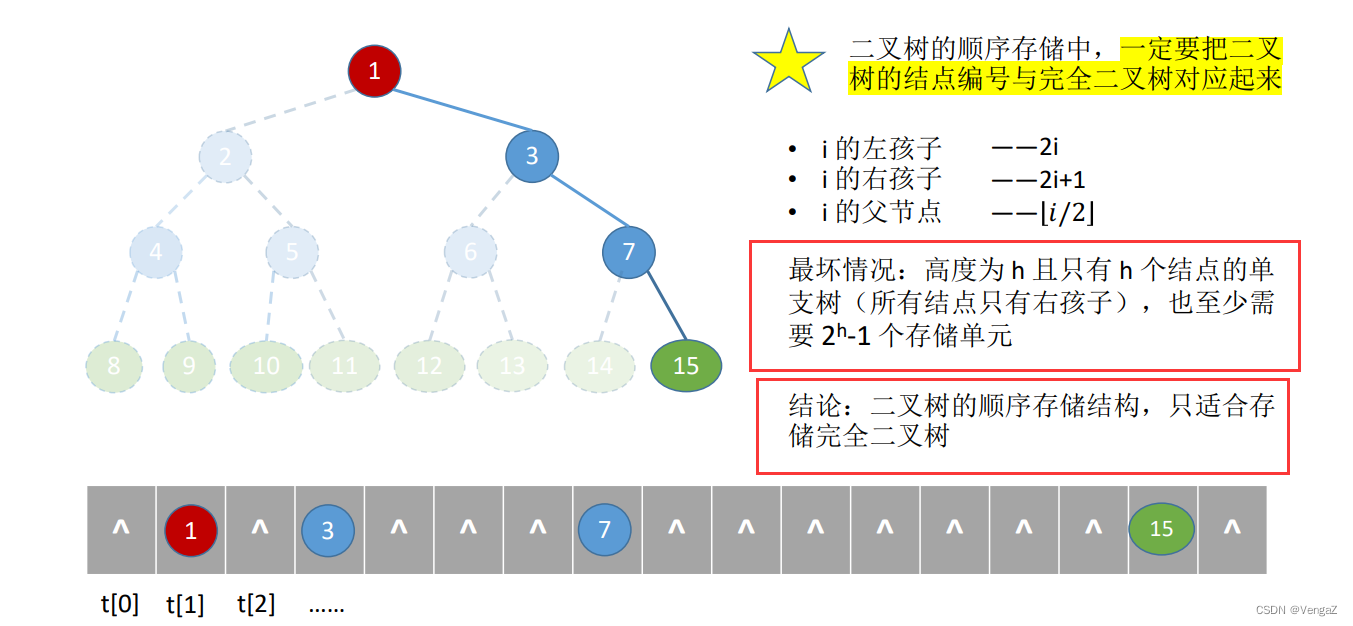
二叉树的顺序存储中,一定要把二叉树的结点编号与完全二叉树对应起来;
非完全二叉树
2. 链式存储
每个节点有两个指针域,n个节点就有2n个指针域,但是只有n-1个指针域指向n-1个子节点,所以有n+1个空指针域
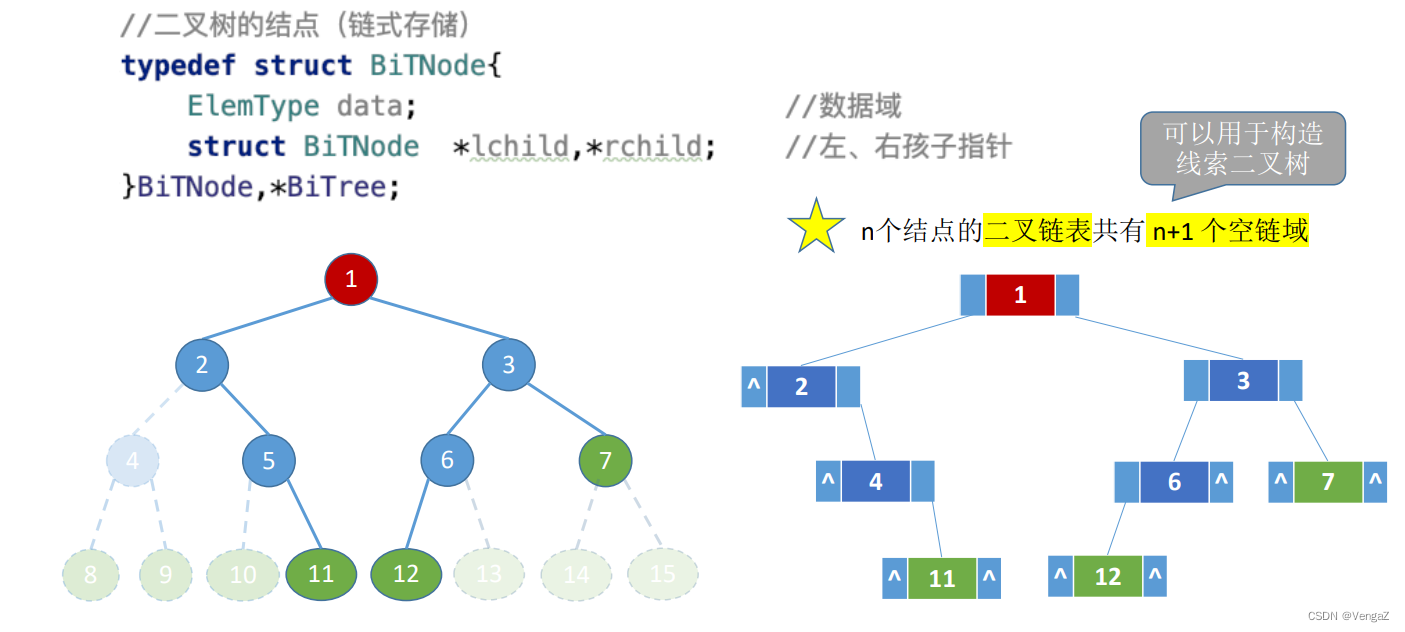
//二叉树的结点
struct ElemType{
int value;
};
typedef struct BiTnode{
ElemType data; //数据域
struct BiTNode *lchild, *rchild; //左、右孩子指针
}BiTNode, *BiTree;
//定义一棵空树
BiTree root = NULL;
//插入根节点
root = (BiTree) malloc (sizeof(BiTNode));
root -> data = {1}; //{}是必须的,因为这里对结构体初始化
root -> lchild = NULL;
root -> rchild = NULL;
//插入新结点
BiTNode *p = (BiTree) malloc (sizeof(BiTNode));
p -> data = {2};
p -> lchild = NULL;
p -> rchild = NULL;
root -> lchild = p; //作为根节点的左孩子
逆向寻找父节点
三叉链表