层次分析法

文章目录
- 层次分析法
- 评价类问题可以用打分来解决
- 1.通过查阅资料选定指标
- 2.画出权重表格并填写
- 2.1.判断矩阵
- 一致矩阵
- 2.3一致性检验的步骤
- 先算一致性指标CI
- 根据表格查找n对应的RI(平均随机一致性指标),表格一般会在题目中给出
- 计算一致性比例CR
- 若得出CR<0.1,判断说明判断矩阵的一致性可以接受;若CR>=0.1,判断说明矩阵的一致性不能接受,需要对判断矩阵进行纠正。
- 3.计算判断矩阵权重
- 3.1算数平均法计算权重
- 权重进行归一化处理
- 若判断矩阵是一致矩阵,任选一列计算权重
- 若判断矩阵不是一致矩阵,对不同列分别计算权重,最后计算平均权重
- 3.2几何平均法求权重
- 3.3特征值法求权重
- 若判断矩阵为一致矩阵,其特征值为n,其余特征值为0
- 3.4最后将计算结果填入权重表格
- 4.汇总结果得到权重矩阵
- 5. 计算各方案的得分
- 层次分析法在论文中体现的步骤
- 层次分析法的局限性
- 算数平均法计算权重代码
- 几何平均法求权重代码
- 特征值法求权重代码
- 计算一致性检验代码
- 计算一致性检验代码
提示:资料可以从知网,万方,百度学术,谷歌学术等平台上搜索

评价类问题可以用打分来解决
评价类问题应该从这三个方面中切入
- 我们评价的目标是什么?
- 我们为了达到目标有哪些选择方案?
- 评价的指标是什么?
- 前两个问题可以在题目中得出,第三个问题要通过提炼题目或者搜索得出
- 总结一下:通过题目得出我们评价的目标是什么,然后推断出几种选择方案,再通过评价的指标給选择方案打分,最终选择出最优方案。
通过查找资料对比得出权重

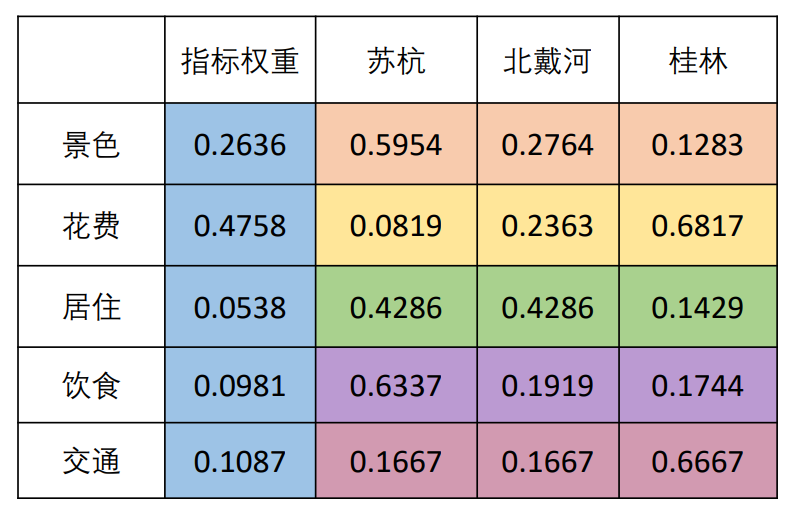
- 计算得出指标对应权重,指标权重加起来为1;然后根据对象查找指标定义权重得分,根据不同对象的横向对比得出不同对象的同一指标权重得分,其中同一个指标的得分相加为1;最后用对对象的得分*指标权重加总求和,选出最大总和的对象
接下来通过分析题目推导层次分析法的步骤
- 小明同学想去旅游,在网上查阅攻略后,选定了苏杭,北戴河,桂林三处名胜作为旅游景点,请通过确定评价指标、形成评价体系来为小明同学选择最佳的方案。
1.通过查阅资料选定指标

现在我们来回答一下评价类问题的三个切入问题
- 我们评价的目标是什么?
为小明同学选择最佳的旅游景点
- 我们为了达到这个目标有哪几种可选的方案?
三种,分别是去苏杭、去北戴河和去桂林
- 评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
景色、花费、居住、饮食、交通
2.画出权重表格并填写
- 先做出该表格然后一一分析填空
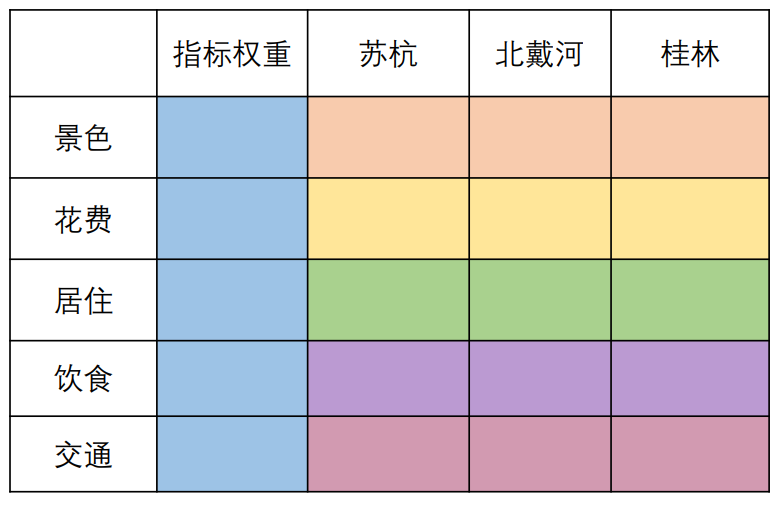
- 因为这里关系到三个景点和五种指标,若一起进行分析的话会非常困难,因此在这里我们只需要两两指标比较,根据比较结果推算出权重。也因此有了下面这个两两比较表示重要程度的表格

2.1.判断矩阵
- 根据两两指标比较得出的结果可以作出一个表格,该表格被称为判断矩阵。
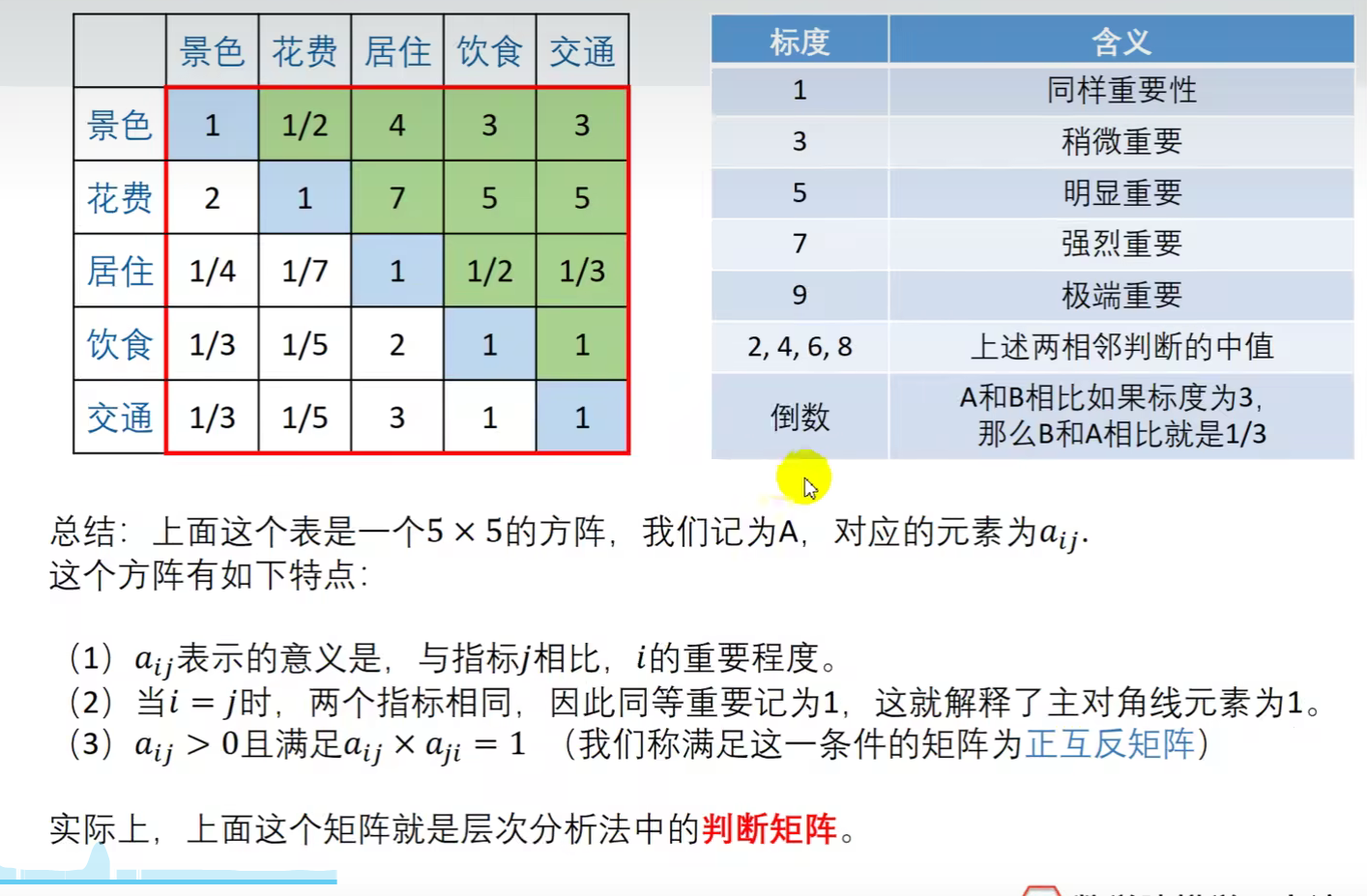
-
根据所得资料将两两对象的指标相互比较,得出对应的元素aij(指标i与指标j相比i的重要程度),然后作出该矩阵
-
该矩阵若满足:
- i==j时即两指标相同因此aij相同记为1
- aij>0且aijxaji=1
那么将这样的矩阵称为正互反矩阵,这个矩阵在层次分析法中作为判断矩阵(如a13就可以表示为景色的重要程度比居住要介于稍微重要和明显重要之间。)
此时小明根据两两指标对比得出结果,依次填到判断矩阵中。但实际上我们参加比赛的时候不会有小明帮我们填,需要我们通过查找资料,计算,推断得出结果。
另外判断矩阵满足某些条件后是一致矩阵,一致矩阵是判断矩阵的一种形式。
一致矩阵

- 能由以下两个公式
a i j = i 的重要程度 / j 的重要程度, a j i = j 的重要程度 / i 的重要程度 a_{ij}=i的重要程度/j的重要程度,a_{ji}=j的重要程度/i的重要程度 aij=i的重要程度/j的重要程度,aji=j的重要程度/i的重要程度
得出下面的公式
a
i
k
=
i
的重要程度
/
k
的重要程度
=
a
i
j
∗
a
j
k
a_{ik}=i的重要程度/k的重要程度=a_{ij}*a_{jk}
aik=i的重要程度/k的重要程度=aij∗ajk
即在判断矩阵的基础上,满足aijxajk=aik则该矩阵为一致矩阵。根据该公式还能得出该矩阵满足行之间成倍数关系、列之间成倍数关系

- 当判断矩阵是一致矩阵时,特征值=一致矩阵主对角线的加总即为n
- 特征值为n时,对应的特征向量为矩阵的第一行
- 当矩阵不是一致矩阵时,令判断矩阵为行列式,并且主对角线同时减同一个数,令该行列式为0,解出来该数就是该判断矩阵的特征值,特征值可能会有多个解
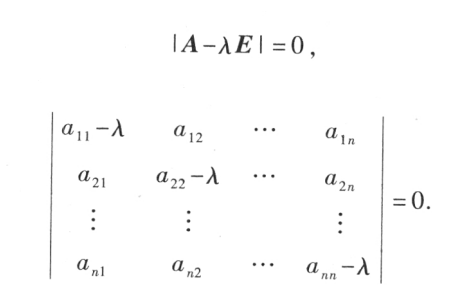
另外可能会有人会把这里提到的正互反矩阵和线性代数中的正交矩阵混淆,这里我说明一下:
正交矩阵和正互反矩阵是两个不同的概念。正交矩阵是一个方阵,其列向量两两正交且长度为1。它的转置矩阵与它本身相乘等于单位矩阵。正交矩阵表示的是线性变换中的旋转和镜像操作,保持向量的长度和间角不变。正互反矩阵是一个对称矩阵,其所有特征值都大于零。它满足对于任意非零向量x,aij>0,其中A为正互反矩阵。正互反矩阵表达的是二次型的正定性,用于描述优化问题中的约束条件或二次型优化的性质。虽然正交矩阵和正互反矩阵在某些特殊情况下可能有一些重叠,但它们的定义和应用领域是不同的。
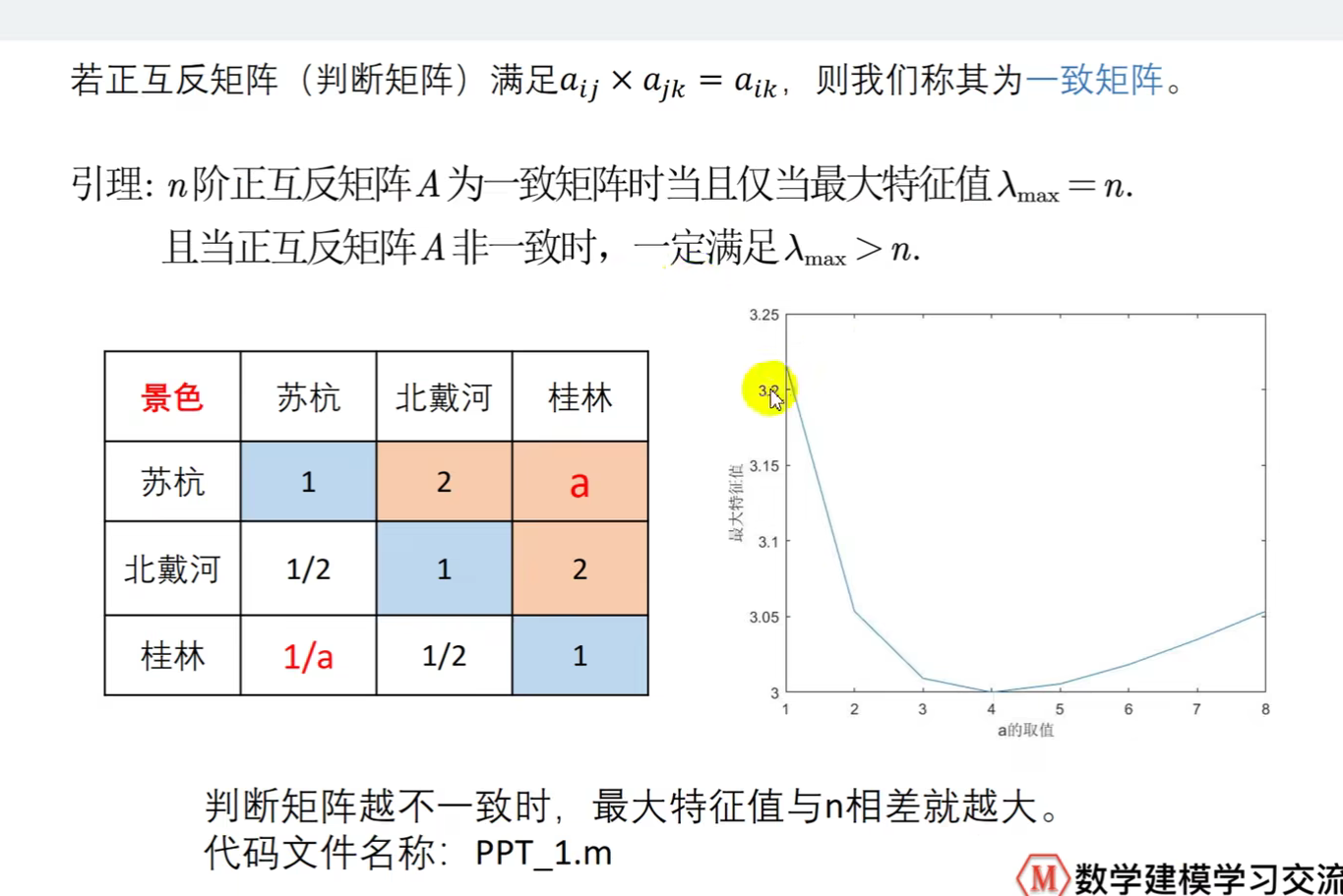
- 当判断矩阵满足aijxajk=aik即判断矩阵是一致矩阵时,最大特征值为n;当判断矩阵不算一致矩阵时,一定满足最大特征值大于n,且矩阵越不一致,最大特征值与n相差越大
- 特征值的计算:令判断矩阵为方阵A,λ
- 以上图为例,当a=4时,此时特征值为3,即是特征值随a变化而变化的最小值
总结一下:
- 两两指标对比画图表得出判断矩阵,判断矩阵的必须满足i==j时即两指标相同既为1;aij>0且aijxaji=1
- 判断矩阵的基础上,矩阵若满足各行(各列)之间成倍数关系,则该矩阵为一致矩阵
- 一致矩阵的特征值为n,当矩阵不是一致矩阵时,,一定满足最大特征值大于n,且矩阵越不一致,最大特征值与n相差越大
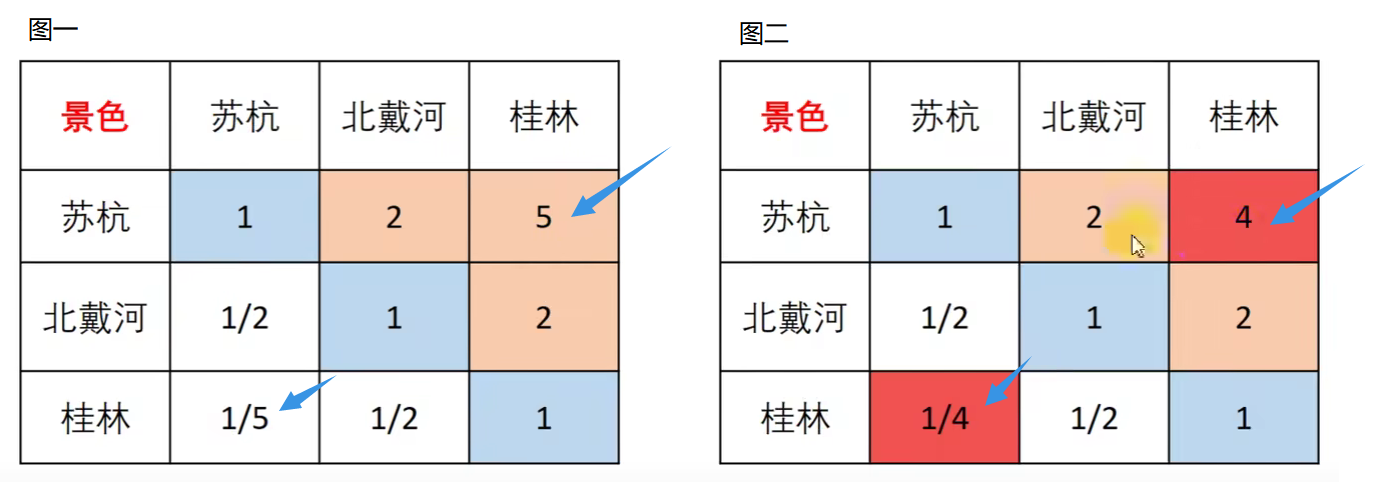
可以看到上图不满足aijxajk=aik所以不算一致矩阵,而图二满足是一致矩阵,那么在使用判断矩阵求权重之前必须对其进行一致性检查。
2.3一致性检验的步骤
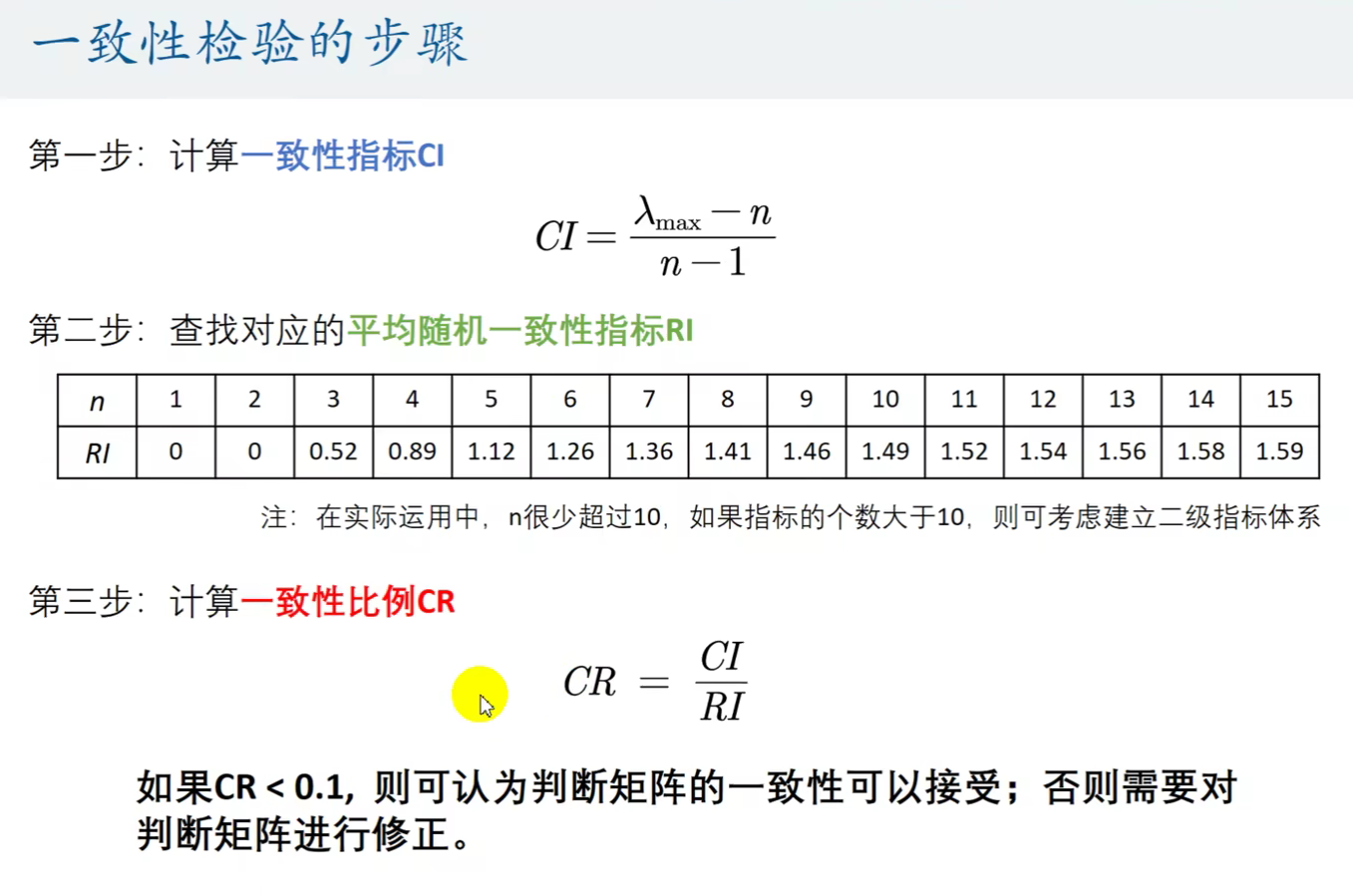
公式如下:
C
I
=
λ
m
a
x
−
n
/
n
−
1
CI=\lambda_{max}-n/n-1
CI=λmax−n/n−1
即为特征值的最大值-矩阵对角线元素的个数除以矩阵对角线元素的个数-1
-
根据表格查找n对应的RI(平均随机一致性指标),表格一般会在题目中给出
-
计算一致性比例CR
公式如下:
C
R
=
C
I
/
R
I
CR=CI/RI
CR=CI/RI
-
若得出CR<0.1,判断说明判断矩阵的一致性可以接受;若CR>=0.1,判断说明矩阵的一致性不能接受,需要对判断矩阵进行纠正。
-
当CR>=0.1时,说明矩阵的一致性不能接受,这时候需要将矩阵往一致矩阵的上调整,既使得矩阵满足各行各列成倍数关系
对判断矩阵进行完一致性检验后,就要对判断矩阵计算权重了
3.计算判断矩阵权重
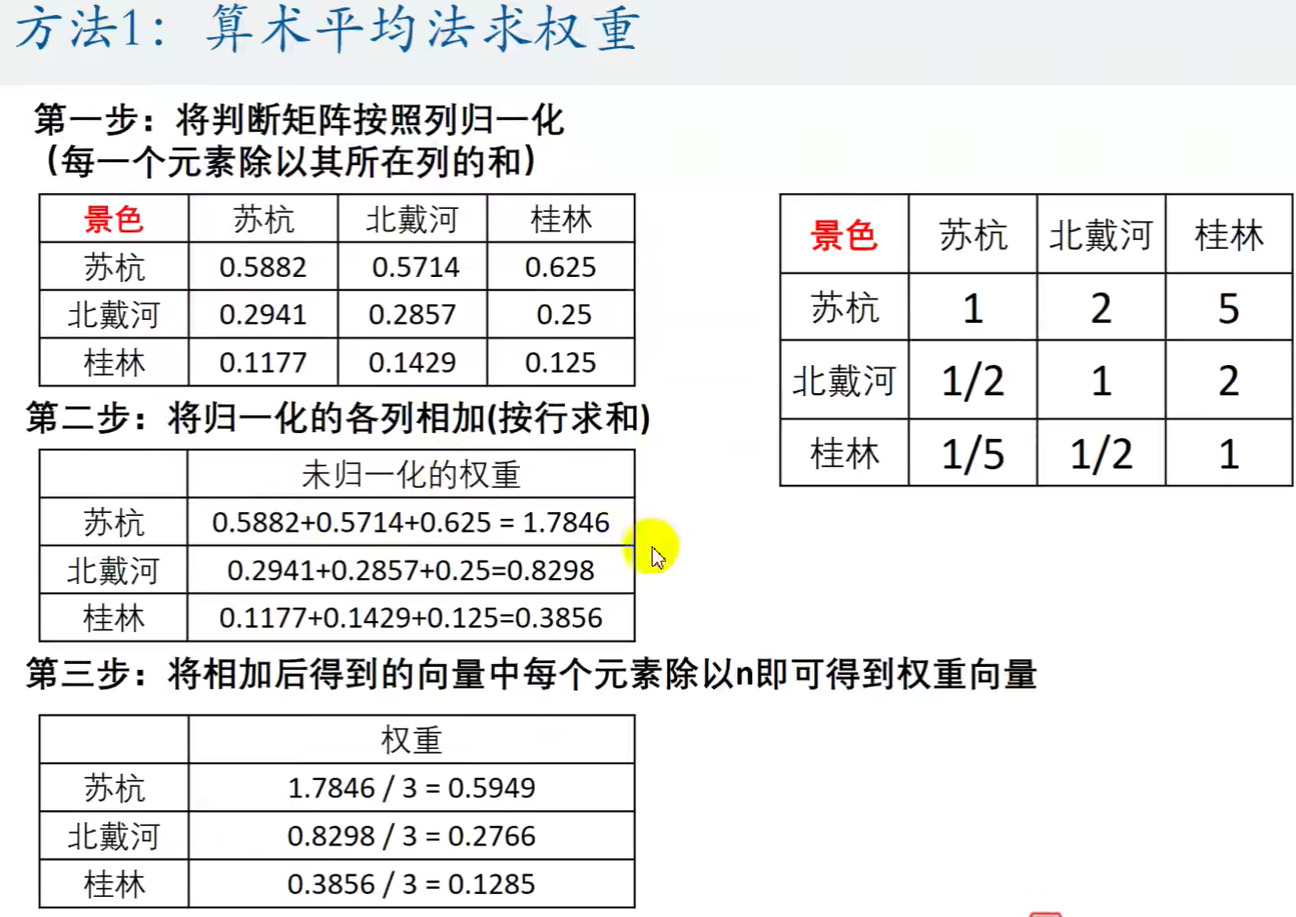
3.1算数平均法计算权重
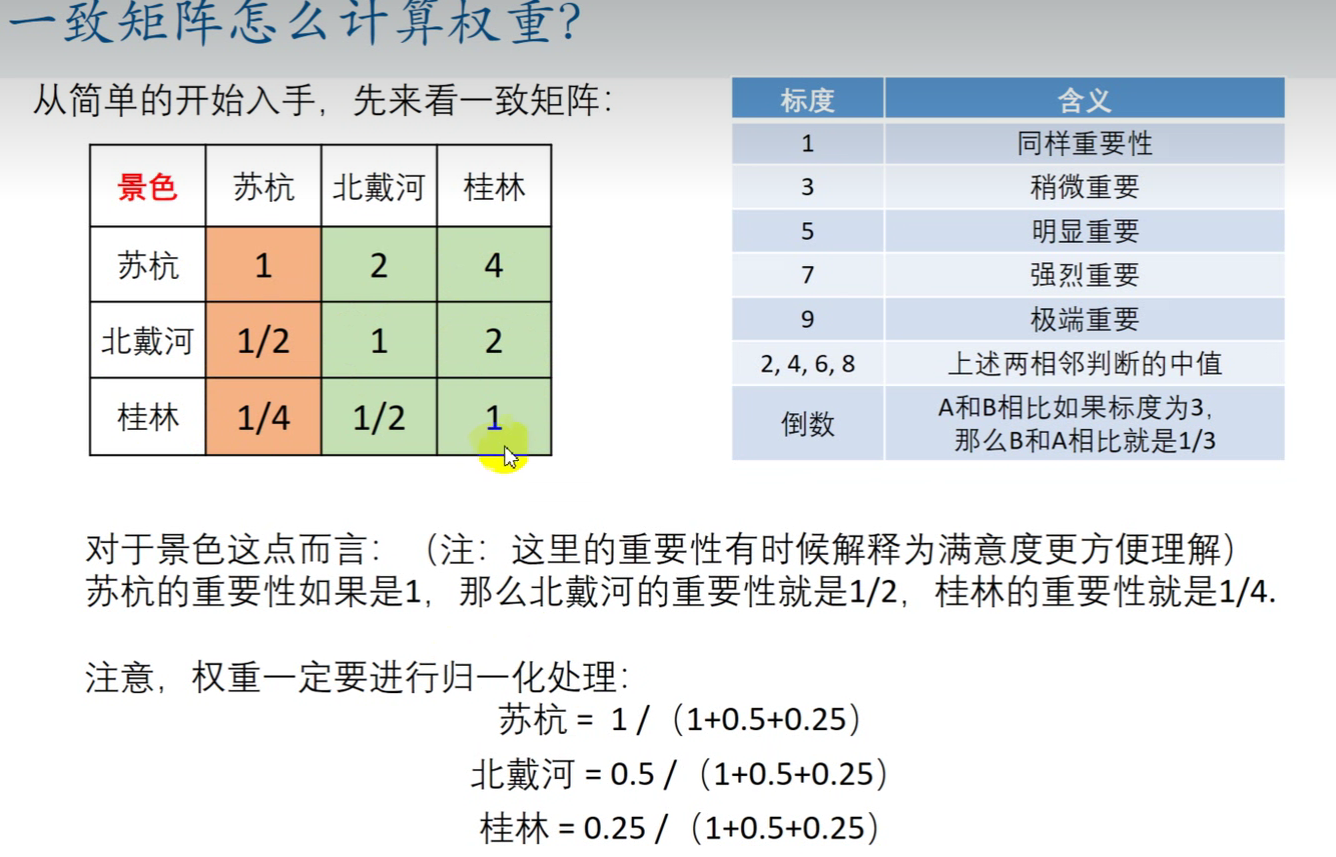
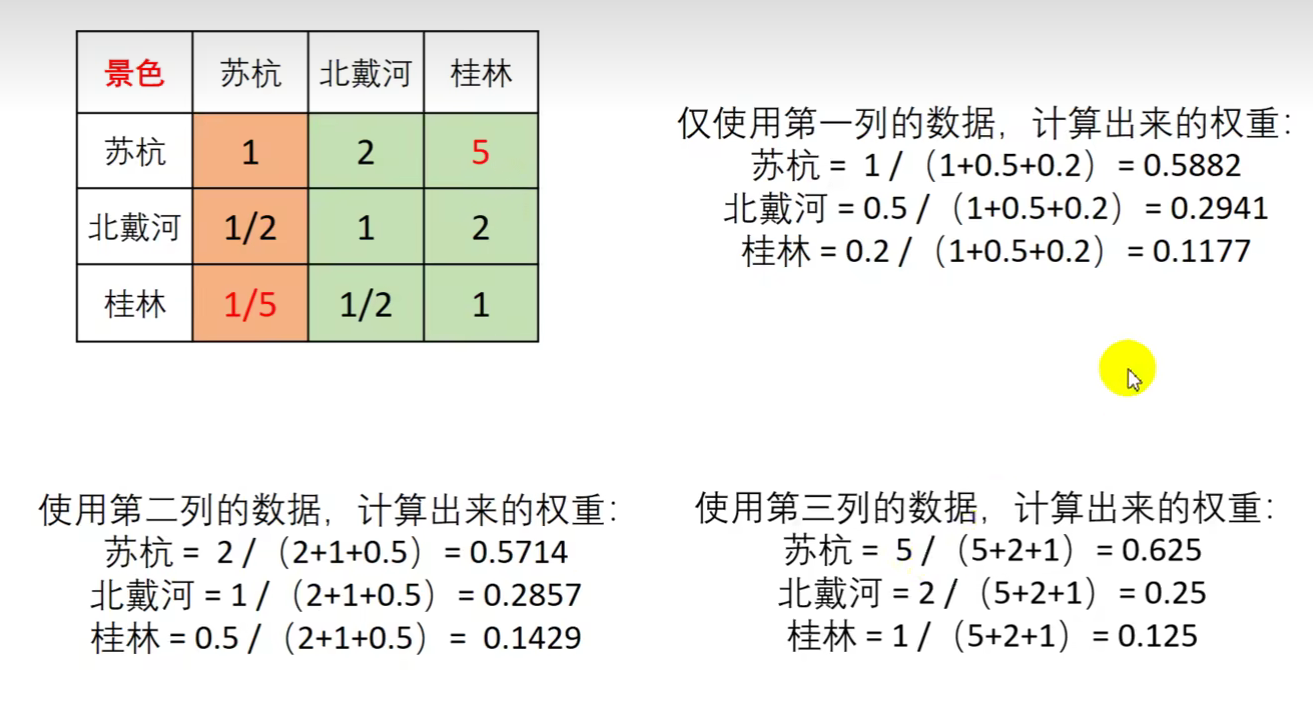
若判断矩阵是一致矩阵,任选一列计算权重
- 若判断矩阵是一致矩阵, 说明行之间成倍数关系,列之间也成倍数关系,所以归一化时选任意一列算出来的结果都是一样的。归一化是指计算某个元素在整个总体的占比。在这里是计算元素在列中的占比
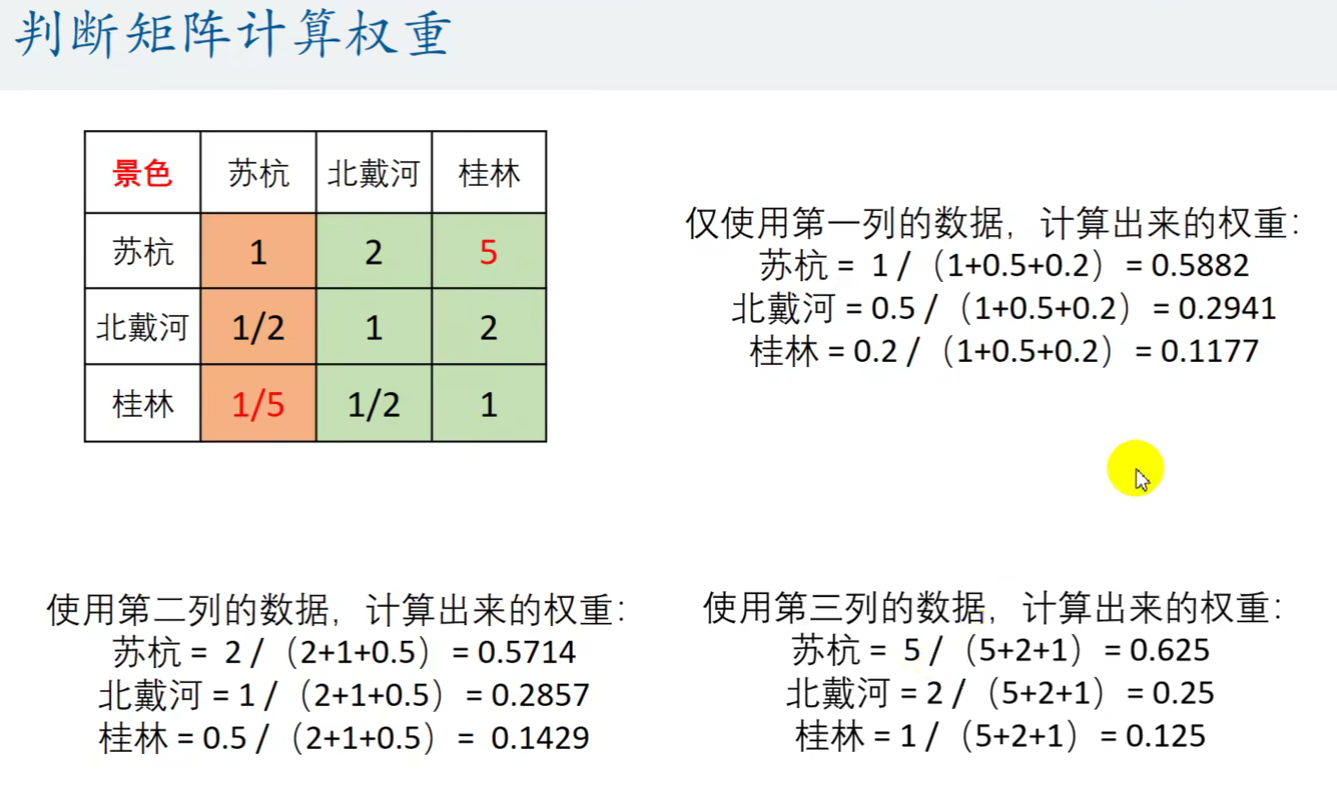
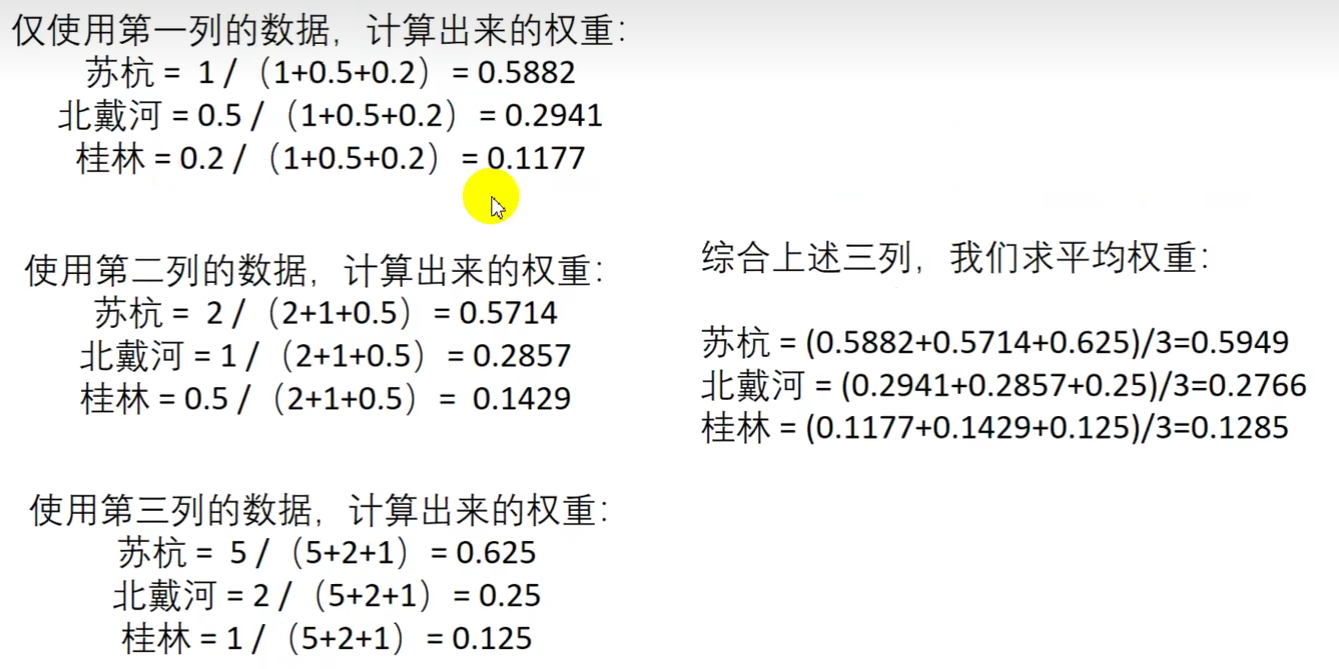
若判断矩阵不是一致矩阵,对不同列分别计算权重,最后计算平均权重
- 若矩阵不是一致矩阵,说明列之间不是成倍数关系,那么每列计算出来的权重并不一样,这时候就需要对全部列分别计算权重,最后求平均权重
总结得出以下步骤和公式:

3.2几何平均法求权重
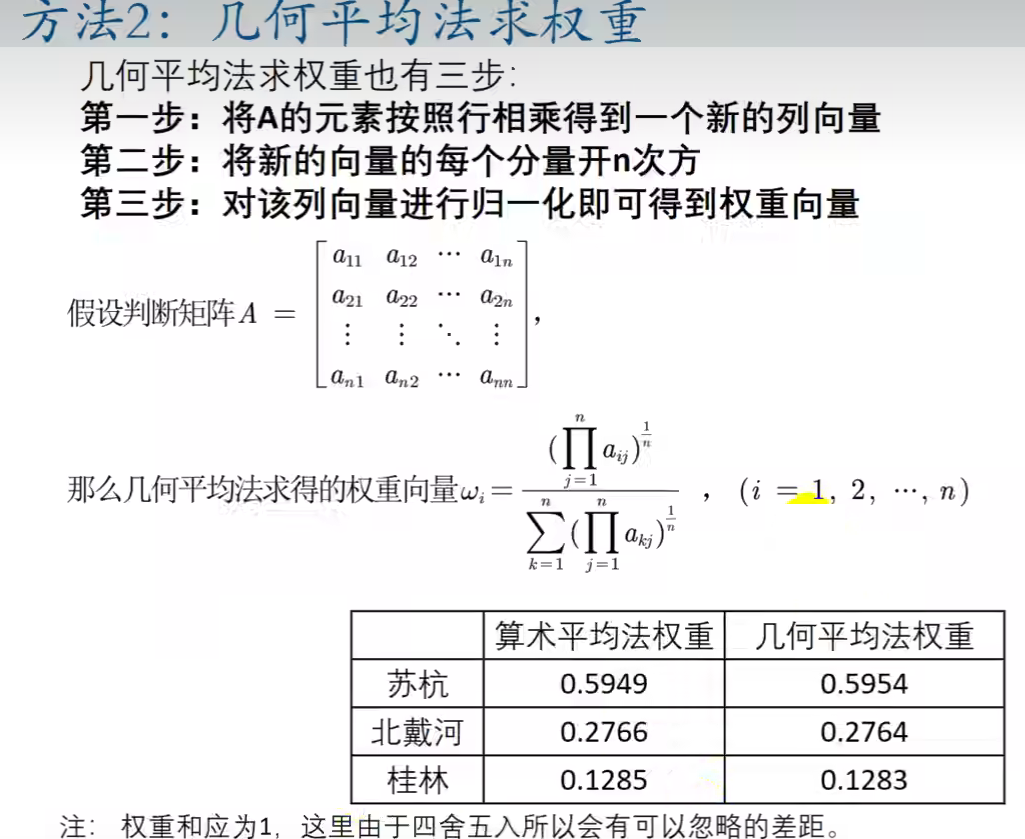
( ∏ j = 1 n a i j ) / ∑ k = 1 n ( ∏ k = 1 n a k j ) 1 / n (\prod^n_{j=1}a_{ij})/\sum^n_{k=1}(\prod^n_{k=1}a_{kj})^{1/n} (j=1∏naij)/k=1∑n(k=1∏nakj)1/n
3.3特征值法求权重
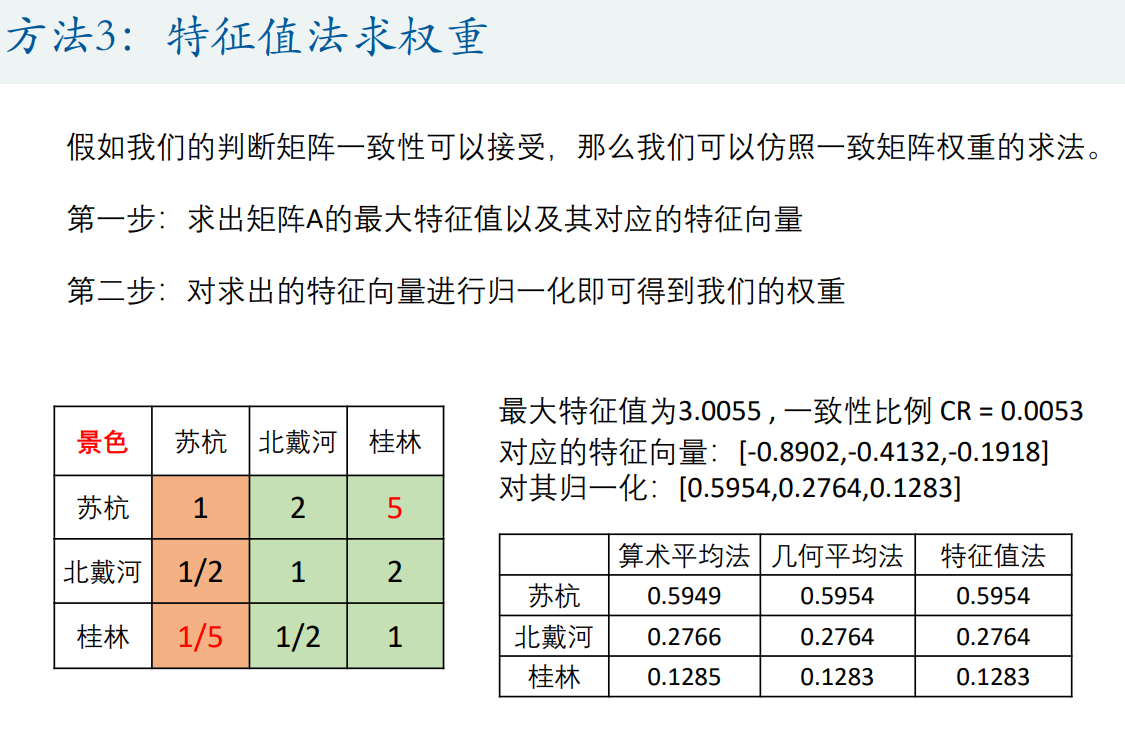
若判断矩阵为一致矩阵,其特征值为n,其余特征值为0
对应的特征向量为一致矩阵的第一列
- 权重归一化:
特征值 / 特征向量 = n / 第一列总和 特征值/特征向量 =n/第一列总和 特征值/特征向量=n/第一列总和
- 另外,若比赛时间足够充裕,建议以上三种计算方法都用上,用上后可以加上一句:为了保证结果的 稳健性,本文采用了三种方法分别求出了权重后计算平均值,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效
3.4最后将计算结果填入权重表格
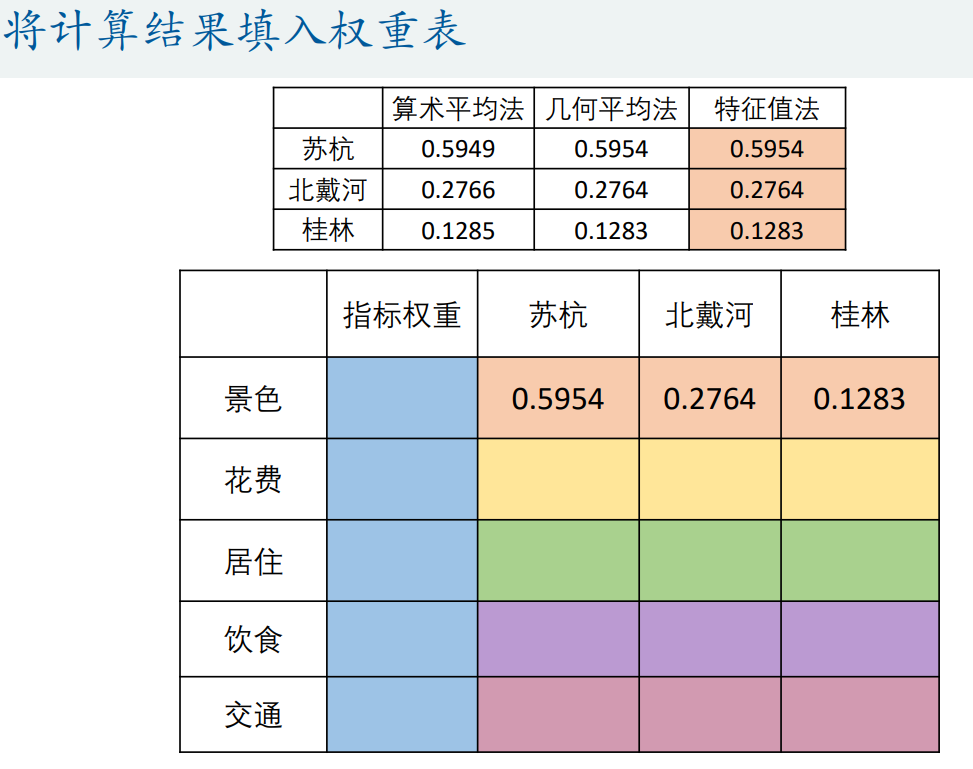
4.汇总结果得到权重矩阵
5. 计算各方案的得分
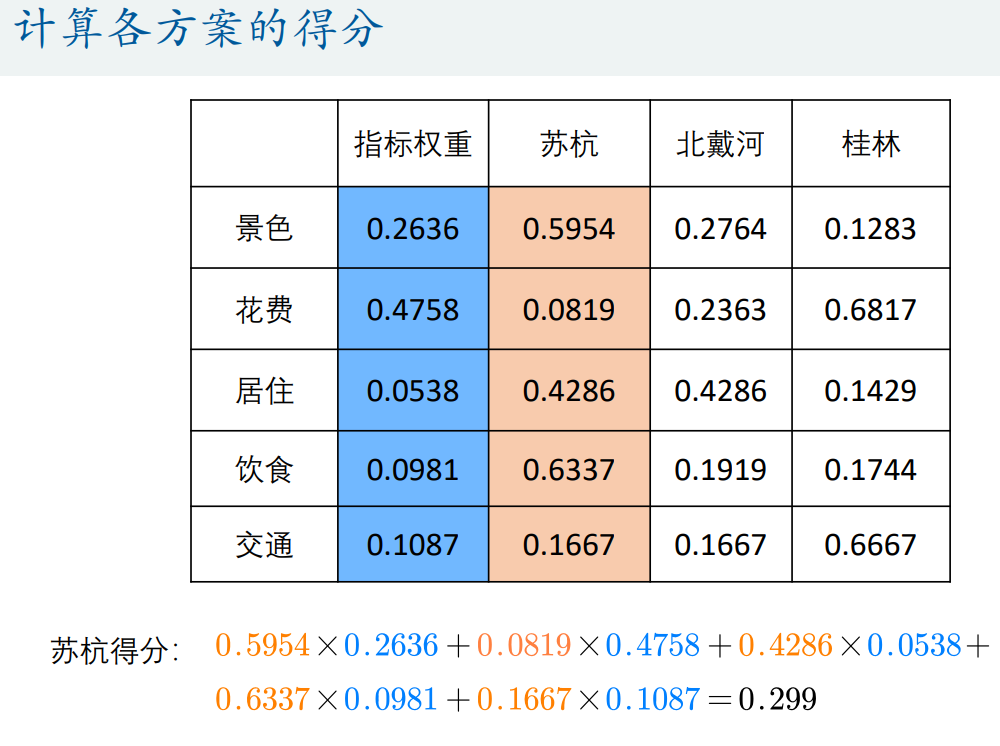
- 根据得分选择分数最高的对象
层次分析法在论文中体现的步骤
总体来说,在论文中体现分为以下几步:
- 分析系统中各因素之间的关系,建立系统的递阶层次结构
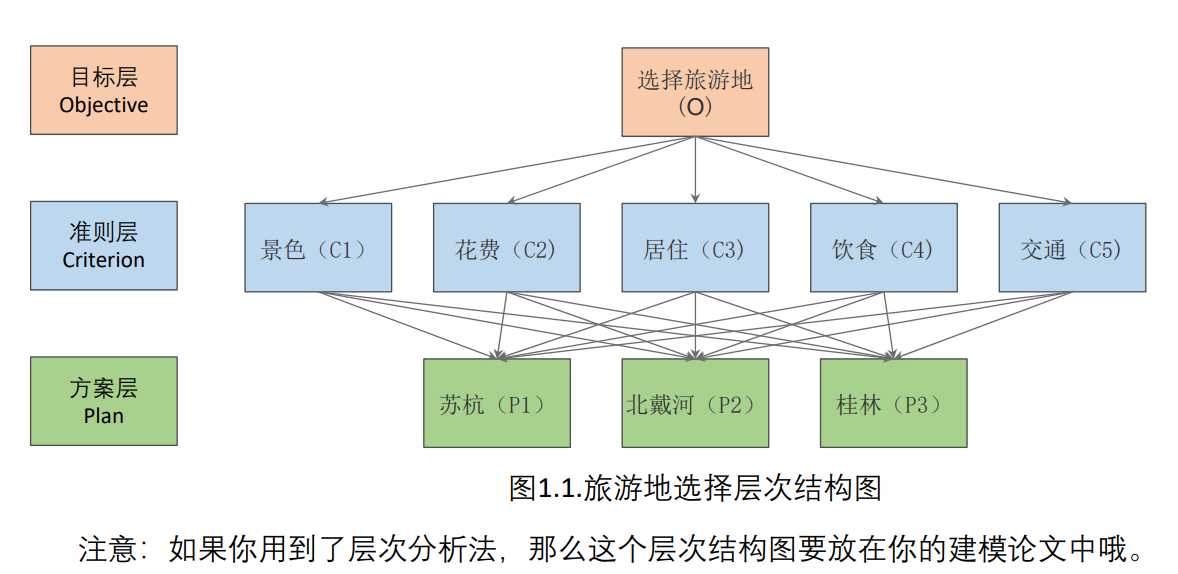
- 该图可以用PPT的smartArt生成,也可以用亿图图示,ProcessOn
具体步骤可以参考如下

- 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)
- 根据判断矩阵两两比较计算得出结果,汇总结果得出权重矩阵
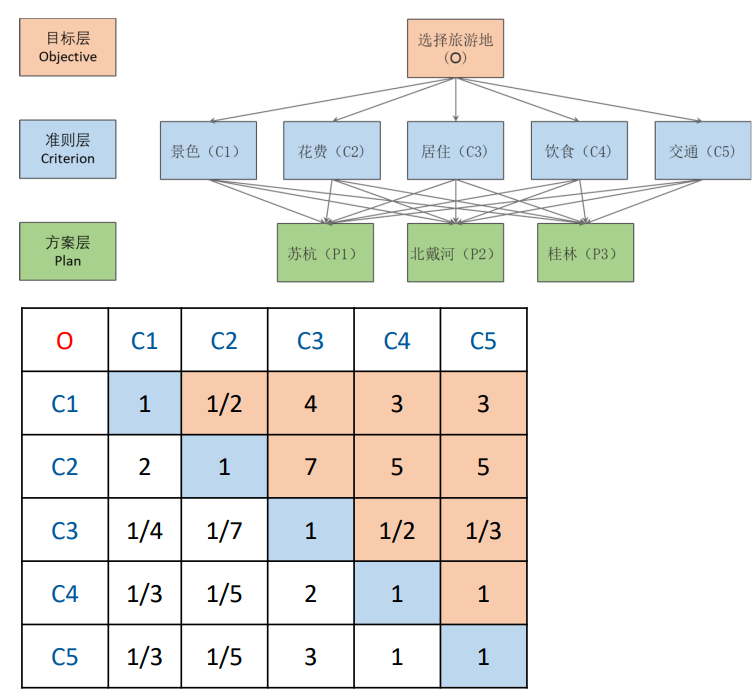
- 根据权重矩阵计算得出最高分数的对象,选择该最高分对象作为最终目标
层次分析法的局限性
- 评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异 可能会很大,平均随机一致性指标RI的表格中n的个数最多是15
- 若决策层中指标的数据是已知的,那么我们如何利用这些数据来使得评价的更加准确呢?我们使用层次分析法是通过查找数据计算推导决策层和目标层,然而当决策层中的指标数据是已知的,层次分析法的价值就不再体现,这时候用其他算法会更好
算数平均法计算权重代码

- 先假定矩阵A为判断矩阵,输入matlab中。其中matlab默认显示是小数

- 将矩阵A进行按列求和然后赋值給col_A矩阵
sum(A):对矩阵A进行求和,默认是列向量求和;sum(A,2)表示对行向量求和
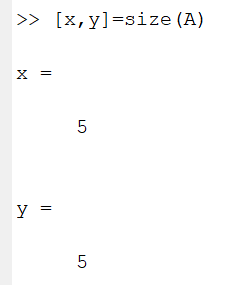
- 根据size函数求得矩阵的行数x和列数y,因为这里矩阵A是方阵,因此x=y
size(A):查看矩阵A的行数和列数
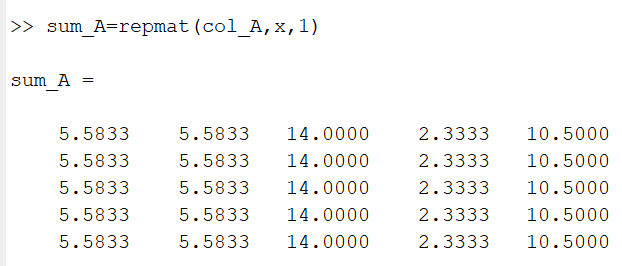
- 将求和矩阵col_A的行数设置为A矩阵的行数,即为后续归一化提供分母
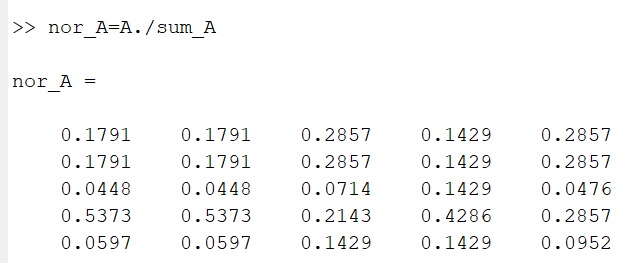
- 将原先的判断矩阵A的各个元素作为分子,把总和矩阵sum_A的各个元素作为分母,进行归一化

- 将归一化的矩阵nor_A按行求和

- 最后求出平均权重
几何平均法求权重代码

- 按行将各个元素相乘,得到一个列矩阵row_A
sum(A):对矩阵A进行求积,默认是列向量求积;sum(A,2)表示对行向量求积

- 求出判断矩阵A的列数n,因为这里的矩阵A是方阵,所以列数=行数=5

- 将列向量row_A的每个元素都开1/n次方得到新的列矩阵den_A

- 将列矩阵den_A的每个元素除以矩阵den_A的总和
特征值法求权重代码

- 求A矩阵的特征向量V和特征值D
E=eig(A),E为特征值;[V,E]=eig(A),V是特征向量,E是特征值,且特征值对应所在的列的特征向量,且E是以对角矩阵的方式呈现
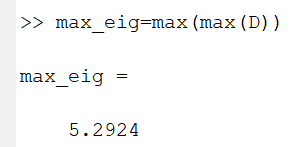
- 求出最大特征值
max(A):对矩阵A求最大:每一列中取最大,返回一个行矩阵。max(max(A)):每列最大中取最大数值

- 求出最大特征值对应的行标r和列标c,即能够根据最大特征值的位置找到对应的特征向量
D == max_eig表示为在矩阵内找到与max_eig相等的元素,找到返回1没找到返回0。[r,c] = find(D == Max_eig , 1)表示:find函数的参数一的返回值与find的参数二1相比较,若相等返回参数一对应结果的行标和列标。

- 找到最大特征值所在的列,该列即为对应的特征向量,然后进行归一化
计算一致性检验代码
C I = λ m a x − n / n − 1 CI=\lambda_{max}-n/n-1 CI=λmax−n/n−1

- Max_eig是最大特征值,由于判断矩阵A是方阵,因此n是矩阵A的行数也是列数

- 根据题目输入一致性指标RI

-
计算一致性比例CR
-
若得出CR<0.1,判断说明判断矩阵的一致性可以接受;若CR>=0.1,判断说明矩阵的一致性不能接受,需要对判断矩阵进行纠正。
对应的特征向量,然后进行归一化
计算一致性检验代码
C I = λ m a x − n / n − 1 CI=\lambda_{max}-n/n-1 CI=λmax−n/n−1
[外链图片转存中…(img-Wu6k78Gr-1690872654596)]
- Max_eig是最大特征值,由于判断矩阵A是方阵,因此n是矩阵A的行数也是列数
[外链图片转存中…(img-OkTUQOkZ-1690872654596)]
- 根据题目输入一致性指标RI
[外链图片转存中…(img-RlICO43U-1690872654596)]
-
计算一致性比例CR
-
若得出CR<0.1,判断说明判断矩阵的一致性可以接受;若CR>=0.1,判断说明矩阵的一致性不能接受,需要对判断矩阵进行纠正。