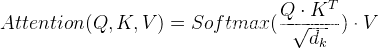2023牛客暑期多校训练营5-B Circle of Mistery

https://ac.nowcoder.com/acm/contest/57359/B

题意

解题思路

感性地想一下，若已有一个环，则再出现其他环就显得多余，所以排列$p$就是$[i,i]$与一个环的结合。
对于序列$a_1、a_2\cdot \cdot \cdot \cdot \cdot \cdot a_x$，只需将它变为$a_2、a_3\cdot \cdot \cdot \cdot \cdot \cdot a_x、a_1$就可构造一个环。考虑该变换所产生的逆序对数：
$a_2\cdot a_1、a_3\cdot a_1\cdot \cdot \cdot a_x\cdot a_1$分别一个逆序数对，对于$i<a_1$或$i>a_x$的数无影响，对于$a_1\le i\le a_x$且$i\ne a_j$
分别有$2$对逆序数对。
设$d{p}_{i,j}$表示前$i$个数选取若干数，共产生$j$对逆序数对，这些数的最大总和为$d{p}_{i,j}$，答案是$d{p}_{i,j}\ge k$时$j$的最小值。得：
$$d{p}_{i,j}=Max(d{p}_{i-1,j-2},d{p}_{i-1,j-1}+a_i)$$

代码

#include<bits/stdc++.h>
using namespace std;
int n,a[1003],ans=0x3f3f3f3f,k,dp[1003][3003];
int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	if(k<=0){
        for(int i=1;i<=n;i++)
		if(a[i]>=k){cout<<0;return 0;}
        cout<<-1;
        return 0;
    }
	for(int i=1;i<=n;i++){
		dp[i][0]=a[i];
		for(int j=1;j<i*2-1;j++)dp[i][j]=max(dp[i-1][j-2],dp[i-1][j-1]+a[j]);
		for(int j=0;j<i*2-1;j++)if(dp[i][j]>=k)ans=min(ans,j);
	}
	if(ans!=0x3f3f3f3f)
	cout<<ans;
	else cout<<-1;
}