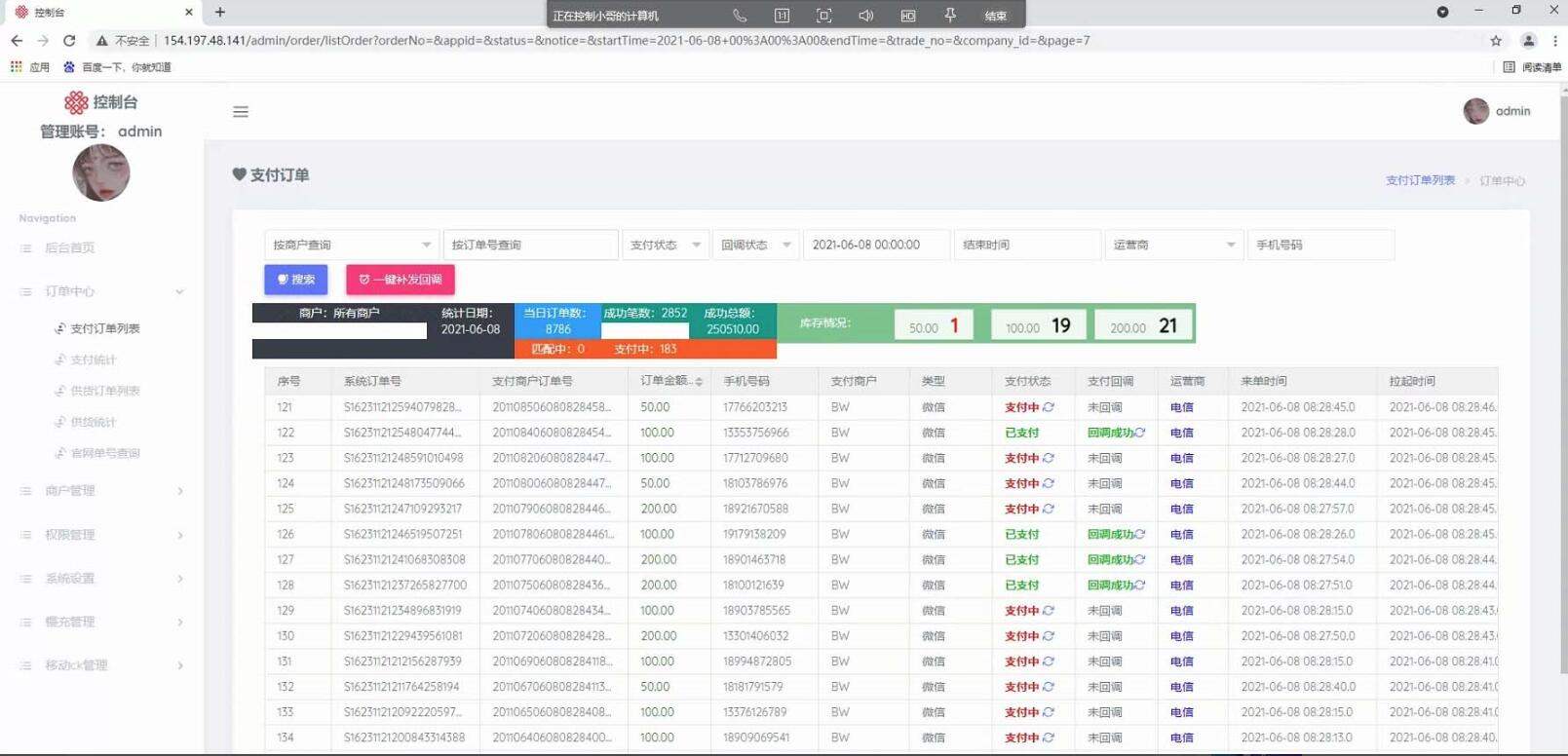
基础的二叉树用的其实不多,二叉树的重点在二叉树的延伸:二叉搜索树。二叉搜索树又延伸出了平衡二叉搜索树。搜索数的特点是:查找效率极高。
二叉搜索树的作用:
1. map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
2. 二叉搜索树的特性了解,有助于更好的理解map和set的特性
3. 二叉树中部分面试题稍微有点难度,在前面讲解大家不容易接受,且时间长容易忘
4. 有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻烦
搜索二叉树的概念
二叉搜索树又称二叉排序树(称为排序树是因为如果采用中序遍历二叉树,得到的是升序排列,正常排序还是排序算法更适合),它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
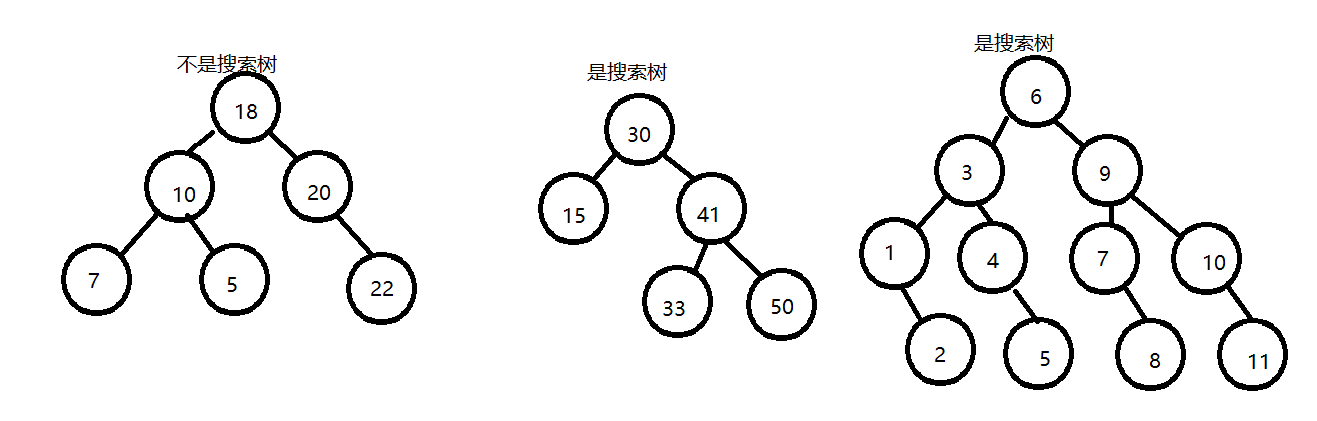
总结一下就是任意一个子树都要满足左子树中的值< 根 < 右子树中的值。
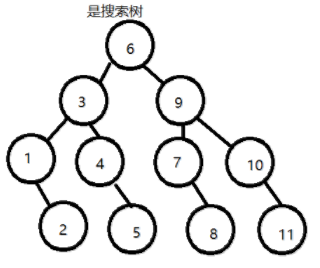
以图示搜索树为例,如果要找8,8比6大,必然在6的右子树,8比9小,必然在9的左子树,8又比7大,在7的右子树,找到8。效率很高。最多查找高度次。有一个误区:虽然搜索树查找效率很高,但是时间复杂度不是O(logN),而是O(N)。因为存在二叉树只有左子树,左节点的情况。如果要达到O(logN)的效果,就要尽量让根节点的左右子树个数差不多,方案有两种:AVL树和红黑树,如何达到这样的效果之后会讲到。
下面先实现搜索树:
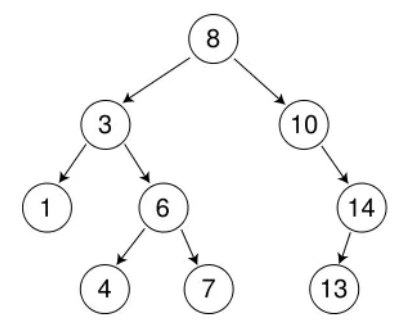
用上图作样例。
BinarySearchTree.h中:
#pragma once
#include<iostream>
#include<vector>
using namespace std;
template<class K>
struct BinarySearchTreeNode
{
BinarySearchTreeNode<K>* _left;
BinarySearchTreeNode<K>* _right;
K _key;
BinarySearchTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BinarySearchTree
{
public:
typedef BinarySearchTreeNode<K> Node;
//编译器向上查找,typedef必须在Destory上面
private:
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
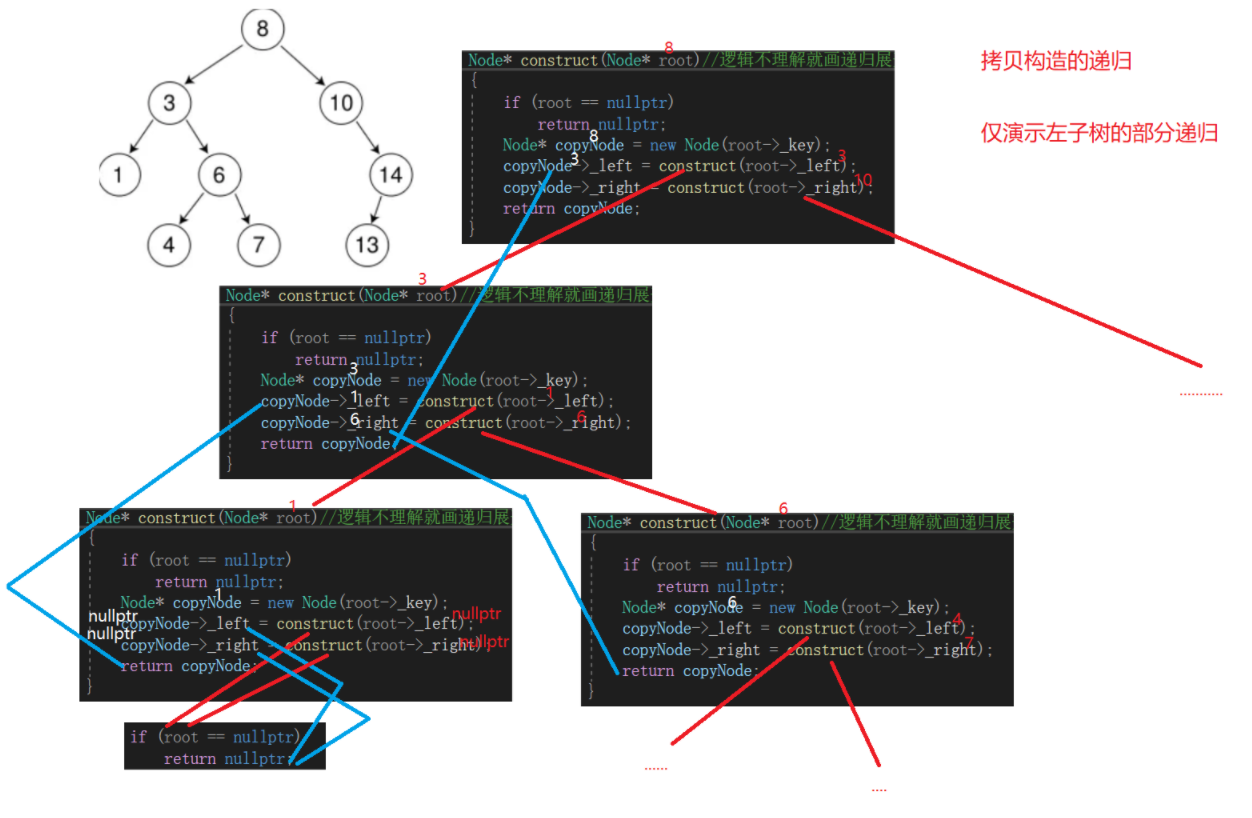
Node* construct(Node* root)
//逻辑不理解就画递归展开图,在文章结尾,有各个函数的递归展开图
{
if (root == nullptr)
return nullptr;
//第一次写的失败作
//root->_left = construct(root->_left);
//root->_right = construct(root->_right);
//return new Node(root->_key);
Node* copyNode = new Node(root->_key);
copyNode->_left = construct(root->_left);
copyNode->_right = construct(root->_right);
return copyNode;
}
public:
//有了拷贝构造,编译器不会自动生成默认构造函数,需要自己手写;
//或者可以通过c++11提供的关键字default完成显示生成默认构造函数BinarySearchTree() = default;
//BinarySearchTree()
// :_root(nullptr)
//{}
BinarySearchTree() = default;
//作用是强制编译器自己生成默认构造函数
BinarySearchTree(BinarySearchTree<K>& tree)
//拷贝构造,需要深拷贝,且无法使用现代写法
{
_root = construct(tree._root);
//拷贝构造自身的参数是BinarySearchTree,只有一个成员参数,不适合递归传参
}
BinarySearchTree<K>& operator=(BinarySearchTree<K> tree)
//拷贝构造完成后,赋值运算符重载一定能使用现代写法
{
swap(_root, tree._root);
return *this;
}
~BinarySearchTree()
//任何递归都需要参数,这里要递归释放空间,就需要传参,所以要通过封装完成空间释放
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const K& key)
//搜索二叉树的结果和插入的顺序有关,如果以一个相对有序的顺序插入数据,树的高度就会接近数据的个数
{
Node* tmp = new Node(key);
if (_root == nullptr)
{
_root = tmp;
return true;
}
else
{
Node* cur = _root;
//cur找key节点所在的位置
Node* parent = nullptr;
//parent记录cur的父节点,在key找到对应位置后,进行对key的链接
while (cur)
//cur停下来时一定在一个空节点
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
//不能插入相同的数,搜索二叉树默认不允许重复的值。
return false;
//也存在允许重复的情况,这时候就统一将重复的值放在左节点/右节点(左右任意,但必须统一)
}
if (parent->_key > key)
//cur找到位置后,需要再确定是parent的左节点还是右节点。
{
parent->_left = tmp;
}
else
{
parent->_right = tmp;
}
}
return true;
}
bool find(const K& key)
//find也可以直接返回节点,但必须被const修饰,原因在于搜索二叉树节点一旦被修改,新的树就可能不是搜索二叉树
{
Node* tmp = _root;
while (tmp)
//逻辑和插入相同
{
if (tmp->_key == key)
{
return true;
}
else
{
if (tmp->_key > key)
{
tmp = tmp->_left;
}
else
{
tmp = tmp->_right;
}
}
}
return false;
}
void InOrder()
//中序遍历需要套一层,因为c++实现封装,外部无法拿到_root的数据
{
_InOrder(_root);
cout << endl;
}
bool Erase(const K& key)
//非递归版本
//搜索二叉树的删除比较复杂,需要画图理解
//搜索二叉树的删除主要分三种情况:删除的节点没有左子树,删除的节点没有右子树,删除的节点有左右子树
//没有左右子树可以归为没有左子树或者没有右子树的情况
{
Node* cur = _root;
Node* parent = nullptr;
//如果_root只有左子树或者只有右子树,且要删除的是根节点,parent的值就不会改变,
//如果parent被初始化成nullptr,在下面parent->_key就会报错,所以进入左为空,或者右为空的判断时,
//要添一部分代码,保证不会走到parent->_key
while (cur)
//首先找到要删除的节点
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
break;
}
if (cur == nullptr)
//没找到删除的节点,或者树中没有节点
return false;
if (cur->_left == nullptr)
//删除的节点没有左子树,此时让parent节点的左指针或者右指针指向删除节点的右子树就可以
{
if (cur == _root)
//左为空,且删除的是根节点的情况,也是添加代码的部分
{
_root = cur->_right;
//改变根节点的位置
delete cur;
return true;
}
else
//删除的不是根节点
{
if (cur->_key > parent->_key)
{
parent->_right = cur->_right;
delete cur;
//节点是new出来的
return true;
}
else
{
parent->_left = cur->_right;
delete cur;
return true;
}
}
}
else if (cur->_right == nullptr)
//删除的节点没有右子树,逻辑和左子树相同
{
if (cur == _root)
//右为空,且删除的是根节点的情况,添加代码的部分
{
_root = cur->_left;
//改变根节点的位置
delete cur;
return true;
}
else
//删除的不是根节点
{
if (cur->_key > parent->_key)
{
parent->_right = cur->_left;
delete cur;
//节点是new出来的
return true;
}
else
{
parent->_left = cur->_left;
delete cur;
return true;
}
}
}
else
//删除的节点具有左子树和右子树,这时需要通过特殊的方式删除节点
//找到删除节点左子树中最大的节点,或者右子树中最小的节点,替换原来节点中_key的值,再删除找到的节点
//只有左树的最大节点才能比所有左树节点大,才能替换掉被删除的节点;右树的最小节点同理。
//找到的节点一定存在一个子树为空,此时情况和上面情况相同
{
Node* parentTmp = cur;
//cur本来就是tmp的父节点,直接赋值给parentTmp
Node* tmp = cur->_left;
//找到左子树中的最大节点,tmp此时为左子树的根节点
while (tmp->_right != nullptr)
//根据搜索二叉树的特性,子树中右节点一定比左节点和根节点大,最大节点就是左子树中右节点为空的节点
{
parentTmp = tmp;
tmp = tmp->_right;
}
cur->_key = tmp->_key;
//如果这里选择交换节点,而不是节点中的值,那树整个都会改变,因为节点中还有
//节点与子树的关系,比如将根节点与根的左节点交换,根节点就会变成原树的左节点,树会变成原树的左子树
//而原来的根节点直接无法通过现在的根节点找到。即_root指向的位置改变了。
//如果将根的左节点和右节点互换,那么根存储左节点的内容变成了之前右节点空间的内容,
//储存右节点内容的空间同理,就像是树的左右子树互换了。树将不再是搜索二叉树
//在上一步完成后,有些人会将下面部分的内容替换成return Erase(tmp);目的是,此时tmp代表要删除的节点,
//直接通过Erase删除。这其实是弄混了,Erase的参数类型是const K&,而不是Node*,参数都不对应。
//或者return Erase(tmp->_key),这样也不对,cur->_key = tmp->_key;执行后,树已经不是原来的树了,
//Erase(tmp->_key)找到的是cur->_key的位置(cur->_key = tmp->_key后cur->_key和tmp->_key相同,
//且cur->_key离根节点更近,会先被找到)
if (tmp->_key > parentTmp->_key)
//parentTmp是子树根节点和不是子树根节点,parentTmp的链接位置不同
{
parentTmp->_right = tmp->_left;
delete tmp;
return true;
}
else
{
parentTmp->_left = tmp->_left;
delete tmp;
return true;
}
}
}
/
//下面为各个成员函数的递归版本
bool findR(const K& key)
//递归写起来比非递归简单,但理解复杂,如果有非递归的选择,尽量写非递归。
//如果树的高度太高,会栈溢出(栈空间很小)
{
return _findR(_root, key);
}
bool InsertR(const K& key)
//递归逻辑和finR相同,重点是对引用的理解
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
//递归逻辑和finR相同
{
return _EraseR(_root, key);
}
private:
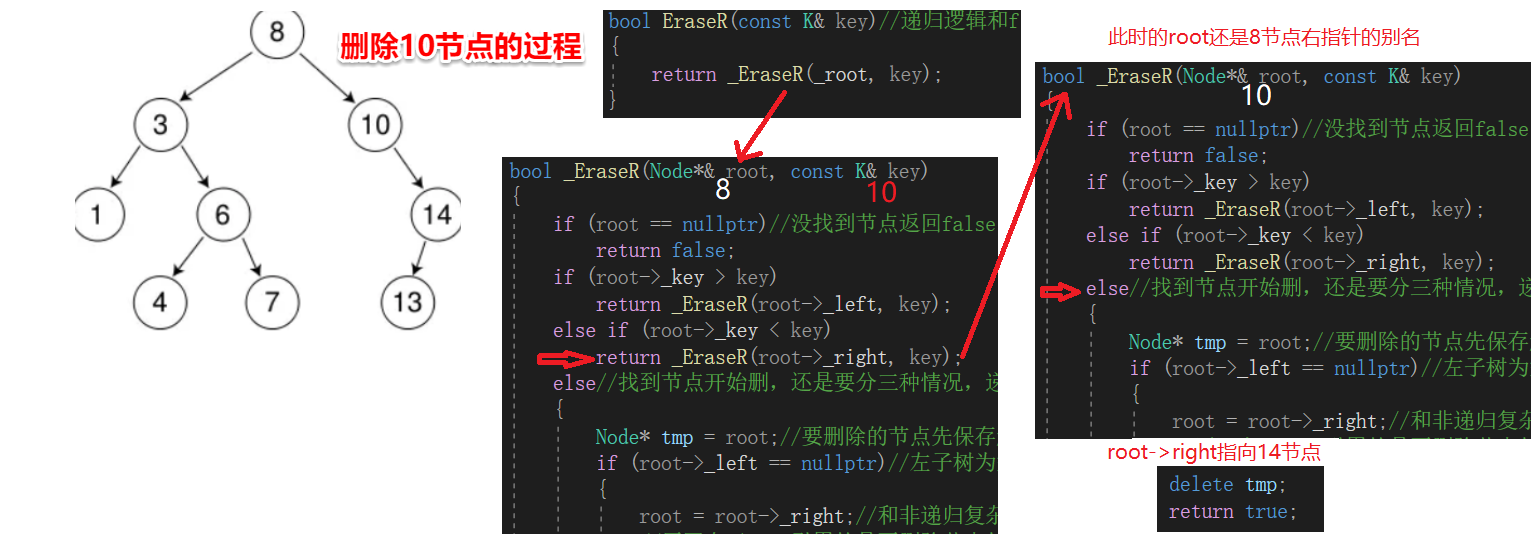
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
//没找到节点返回false
return false;
if (root->_key > key)
return _EraseR(root->_left, key);
else if (root->_key < key)
return _EraseR(root->_right, key);
else
//找到节点开始删,还是要分三种情况,递归只是查找节点的位置
{
Node* tmp = root;
//要删除的节点先保存起来
if (root->_left == nullptr)
//左子树为空的情况
{
root = root->_right;
//和非递归复杂的判断情况不同,这里的递归,利用引用,一句代码就完成了目的
//原因在于root引用的是要删除节点的父节点,指向要删除节点的指针,且左子树为空已经确定
//所以和InsertR一样,root就是链接删除节点右子树的指针,不需要额外的判断。
//还不理解的话看最后的图
}
else if (root->_right == nullptr)
//右子树为空的情况
{
root = root->_left;
//与左子树同理
}
else
{
//以下是选择将要删除节点中的值和找到的值互换,然后删除交换后的目标节点,但有更合适的方法
//tmp = root->_left;
//Node* parentTmp = root;
//while (tmp->_right)
//{
// parentTmp = tmp;
// tmp = tmp->_right;
//}
//swap(tmp->_key, root->_key);
//if (parentTmp->_left == tmp)
// parentTmp->_left = tmp->_left;
//else
// parentTmp->_right = tmp->_left;
Node* minRight = tmp->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
swap(minRight->_key, tmp->_key);
return _EraseR(root->_right, key);
//之前讲过,return Erase(key);无法删除key,但是这里是_EraseR,可以传树的根节点,在新的树中搜索key
//数值交换后,新的树依然满足搜索二叉树,交换的值是右子树的最小值,且比key大,key一定还是新树的最小值
//要删除的节点也只有右子树。
}
delete tmp;
return true;
}
}
//bool _InsertR(Node* root, const K& key)
bool _InsertR(Node*& root, const K& key)
//递归中的神奇之处:root类型改为引用解决父节点问题
{
if (root == nullptr)
//在root为空时,就是创建节点的时候,但是新节点要和树链接上,就需要父节点的左/右指针指向新节点
//父节点可以通过新增一个参数来得到,但是存在更简单的方法:将root参数类型改为引用。在_InsertR的传参中,
//第一个参数是root->_left/root->_right,root是对他们的引用,即root本身就是父节点中指向新节点的指针,
//直接对root赋值,就能将新节点链接上树。
//就算树为空树,root也是对_root的引用,对root的赋值,就可以改变_root。
{
root = new Node(key);
return true;
}
if (root->_key > key)
return _InsertR(root->_left, key);
else if (root->_key < key)
return _InsertR(root->_right, key);
else
return false;
}
bool _findR(Node* root, const K& key)
//最后同样有递归展开图
{
if (root == nullptr)
return false;
if (root->_key > key)
return _findR(root->_left, key);
else if (root->_key < key)
return _findR(root->_right, key);
else
return true;
}
void _InOrder(Node* root)
//中序遍历是递归实现的,必须要有参数
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
Node* _root = nullptr;
};
test.cpp中
//都是测试内容
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinarySearchTree.h"
void BinarySerachTreeTest1()
{
BinarySearchTree<int> t;
vector<int> v;
v.push_back(8);
v.push_back(3);
v.push_back(1);
v.push_back(10);
v.push_back(6);
v.push_back(4);
v.push_back(7);
v.push_back(14);
v.push_back(13);
for (auto e : v)
{
t.Insert(e);
}
t.InOrder();
t.Insert(16);
t.Insert(9);
cout << endl;
t.InOrder();
cout << endl;
bool ret = t.find(0);
cout << ret << endl;
ret = t.find(10);
cout << ret << endl;
ret = t.find(13);
cout << ret << endl;
}
void BinarySerachTreeTest2()
{
BinarySearchTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
cout << endl;
t.Erase(3);
t.InOrder();
cout << endl;
t.Erase(8);
t.InOrder();
cout << endl;
for (auto e : a)
{
t.Erase(e);
}
t.InOrder();
cout << endl;
t.Insert(9);
t.Insert(16);
t.InOrder();
cout << endl;
}
void BinarySerachTreeTest3()
{
BinarySearchTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto e : a)
{
t.Insert(e);
}
BinarySearchTree<int> copy = t;
BinarySearchTree<int> cp;
cp = copy;
}
void BinarySerachTreeTest4()
{
BinarySearchTree<int> t;
int a[] = { 8,3,1,10,6,4,7,14,13 };
for (auto e : a)
{
t.InsertR(e);
}
t.InOrder();
bool ret = t.findR(10);
cout << ret << endl;
ret = t.findR(7);
cout << ret << endl;
ret = t.findR(11);
cout << ret << endl;
t.InOrder();
t.EraseR(8);
t.InOrder();
t.EraseR(3);
t.InOrder();
for (auto e : a)
{
t.EraseR(e);
}
t.InOrder();
}
int main()
{
BinarySerachTreeTest4();
return 0;
}



![[threejs]相机与坐标](https://img-blog.csdnimg.cn/27ae5ed4c134464093ba8240d06ba411.png)


![[Docker实现测试部署CI/CD----相关服务器的安装配置(2)]](https://img-blog.csdnimg.cn/dd0fb3641ac34319b2e118e7082e0e02.png)