文章目录
- 例题列表
- 423. 采药(01背包)
- 1024. 装箱问题(大小和价值相等的01背包)
- 1022. 宠物小精灵之收服(二维费用的背包问题)
- 补充:相关题目——8. 二维费用的背包问题
- 278. 数字组合(01背包问题求方案数)
- 1023. 买书(完全背包求组合数)
- 1021. 货币系统(完全背包求方案数)
- 532. 货币系统(转换成完全背包)🐂好题!
- 6. 多重背包问题 III(多重背包的 单调队列优化)⭐⭐⭐⭐⭐TODO
- 多重背包问题的优化总结⭐!
- 1019. 庆功会(普通分组背包 转换成01背包)
- 7. 混合背包问题(01 + 完全 + 多重 背包)
- 8. 二维费用的背包问题(标准模板题)
- 1020. 潜水员(二维费用的背包问题,装到满足条件的最少重量)🐂 好题!
- 代码优化
- 1013. 机器分配⭐(转换成分组背包问题 + 记录转移路径)
- 但是怎么记下当时的具体分配方案呢?⭐⭐⭐
- 426. 开心的金明(转换成01背包)
- 10. 有依赖的背包问题⭐⭐⭐⭐⭐🚹🐂(树形DP + 分组背包)好题!
- 11. 背包问题求方案数
- 12. 背包问题求具体方案()🐂好题!
- 734. 能量石(贪心 + dp)⭐🐂(重点学习贪心思维!比较相邻两个元素)
- 487. 金明的预算方案(有依赖的状态压缩分组背包DP问题)⭐🐂(好题!)
- 相关链接
例题列表
423. 采药(01背包)
https://www.acwing.com/problem/content/425/

import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int t = sin.nextInt(), m = sin.nextInt();
int[][] g = new int[m][2];
for (int i = 0; i < m; ++i) {
g[i][0] = sin.nextInt();
g[i][1] = sin.nextInt();
}
int[] dp = new int[t + 1];
for (int i = 0; i < m; ++i) {
for (int j = t; j >= g[i][0]; --j) {
dp[j] = Math.max(dp[j], dp[j - g[i][0]] + g[i][1]);
}
}
System.out.println(dp[t]);
}
}
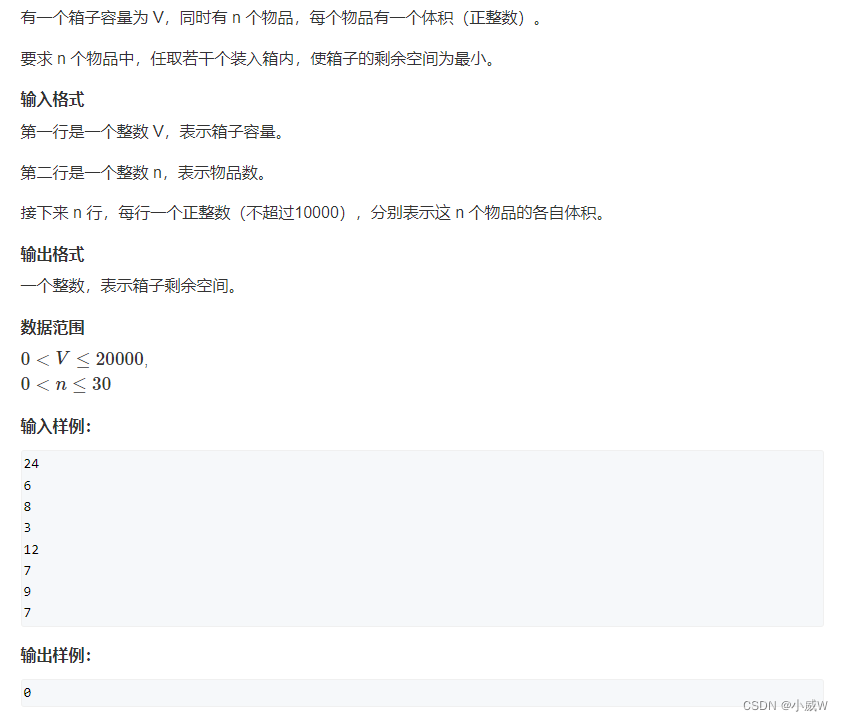
1024. 装箱问题(大小和价值相等的01背包)
https://www.acwing.com/activity/content/problem/content/1268/
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int v = sin.nextInt(), n = sin.nextInt();
int[] dp = new int[v + 1];
for (int i = 0; i < n; ++i) {
int a = sin.nextInt();
for (int j = v; j >= a; --j) {
dp[j] = Math.max(dp[j], dp[j - a] + a);
}
}
System.out.println(v - dp[v]);
}
}
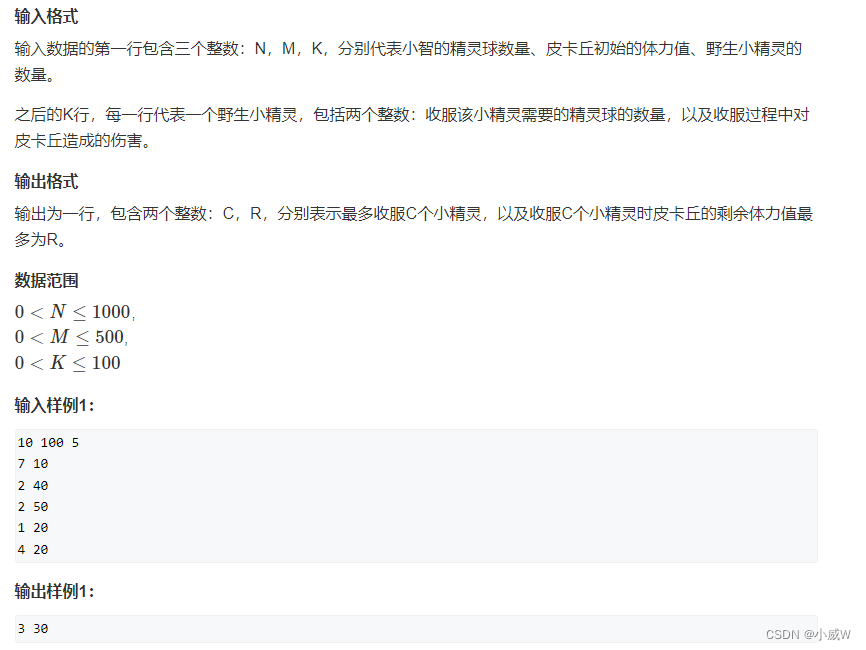
1022. 宠物小精灵之收服(二维费用的背包问题)
https://www.acwing.com/problem/content/1024/

import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt(), k = sin.nextInt();
int[] c = new int[k], h = new int[k];
for (int i = 0; i < k; ++i) {
c[i] = sin.nextInt();
h[i] = sin.nextInt();
}
int[][] dp = new int[n + 1][m];
for (int i = 0; i < k; ++i) {
// 二维背包容量
for (int j = n; j >= c[i]; --j) {
for (int x = m - 1; x >= h[i]; --x) {
dp[j][x] = Math.max(dp[j][x], dp[j - c[i]][x - h[i]] + 1);
}
}
}
System.out.print(dp[n][m - 1] + " ");
// 找到最大健康量
int x = m - 1;
while (x > 0 && dp[n][x - 1] == dp[n][m - 1]) x--;
System.out.println(m - x);
}
}
补充:相关题目——8. 二维费用的背包问题
https://www.acwing.com/problem/content/8/

import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), v = sin.nextInt(), m = sin.nextInt();
int[][] dp = new int[v + 1][m + 1];
for (int i = 0; i < n; ++i) {
int vv = sin.nextInt(), mm = sin.nextInt(), w = sin.nextInt();
for (int j = v; j >= vv; --j) {
for (int k = m; k >= mm; --k) {
dp[j][k] = Math.max(dp[j][k], dp[j - vv][k - mm] + w);
}
}
}
System.out.println(dp[v][m]);
}
}
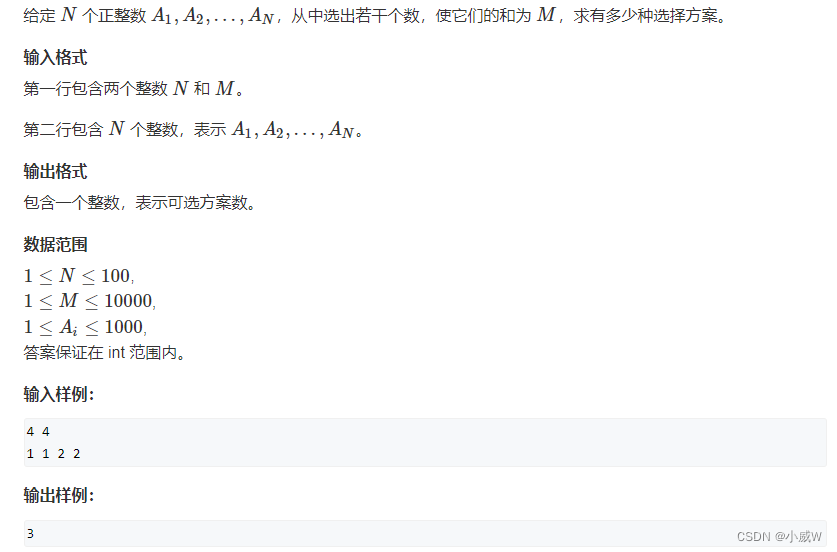
278. 数字组合(01背包问题求方案数)
https://www.acwing.com/problem/content/280/
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
int[] dp = new int[m + 1];
dp[0] = 1;
for (int i = 0; i < n; ++i) {
int a = sin.nextInt();
for (int j = m; j >= a; --j) {
dp[j] += dp[j - a];
}
}
System.out.println(dp[m]);
}
}
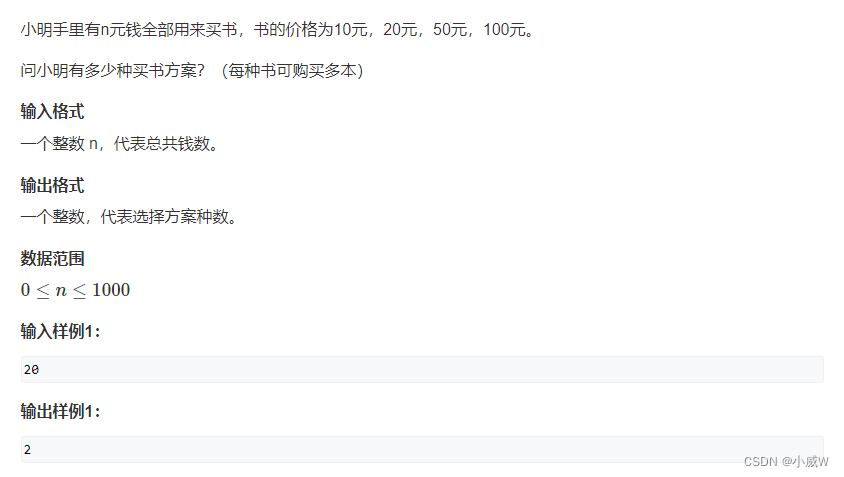
1023. 买书(完全背包求组合数)
https://www.acwing.com/problem/content/1025/
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt();
int[] a = new int[]{10, 20, 50, 100};
int[] dp = new int[n + 1];
dp[0] = 1;
for (int k : a) {
for (int j = k; j <= n; ++j) {
dp[j] += dp[j - k];
}
}
System.out.println(dp[n]);
}
}
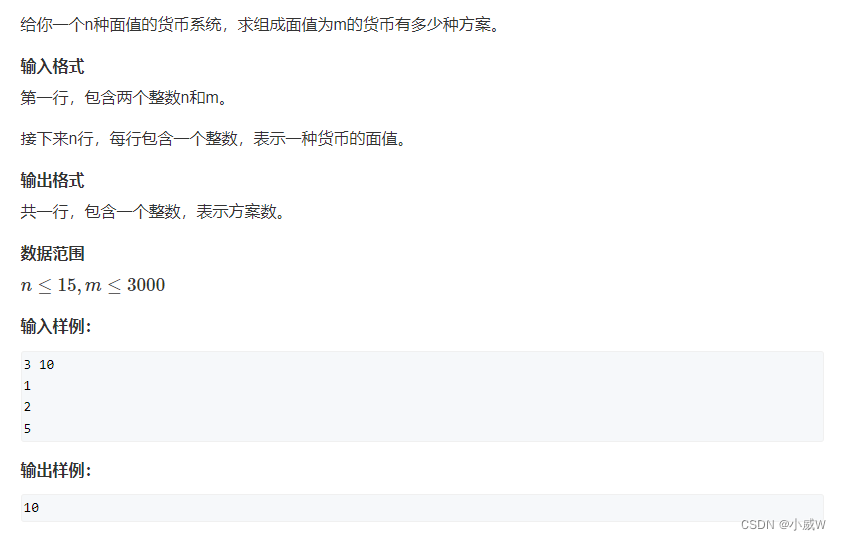
1021. 货币系统(完全背包求方案数)
https://www.acwing.com/problem/content/1023/
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
long[] dp = new long[m + 1];
dp[0] = 1;
for (int i = 0; i < n; ++i) {
int a = sin.nextInt();
for (int j = a; j <= m; ++j) {
dp[j] += dp[j - a];
}
}
System.out.println(dp[m]);
}
}
532. 货币系统(转换成完全背包)🐂好题!
https://www.acwing.com/problem/content/534/

理清题意,一个货币系统有若干面值 x, y, z …。如果其中一个面值可以由其它面值组成的话,那么这个面值就是多余的,可以删掉。
我们可以先排序,然后使用完全背包模型计算各个面值能不能由比它小的那些面值组合而成。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int t = scanner.nextInt();
while (t-- != 0) {
int n = scanner.nextInt(), res = n;
int[] a = new int[n];
for (int i = 0; i < n; ++i) a[i] = scanner.nextInt();
Arrays.sort(a);
boolean[] dp = new boolean[a[n - 1] + 1];
for (int i = 0; i < n; ++i) {
if (dp[a[i]]) --res; // 如果这个面值可以由其它面值组成,那么这个面值就是多余的
dp[a[i]] = true;
for (int j = a[i]; j <= a[n - 1]; ++j) {
dp[j] |= dp[j - a[i]];
}
}
System.out.println(res);
}
}
}
6. 多重背包问题 III(多重背包的 单调队列优化)⭐⭐⭐⭐⭐TODO
https://www.acwing.com/activity/content/problem/content/1274/

在 【算法基础:动态规划】5.1 背包问题 中有多重背包问题的 二进制优化方法。
在这里插入代码片
多重背包问题的优化总结⭐!
多重背包问题——物品的个数是多个,不是无限个。
当作01背包来理解,s个物品当成s次01背包操作——通过二进制来优化。
当作完全背包来理解,就是有数量限制的完全背包——这个数量限制就可以理解成滑动窗口的宽度,通过单调队列来优化。
1019. 庆功会(普通分组背包 转换成01背包)
https://www.acwing.com/problem/content/1021/
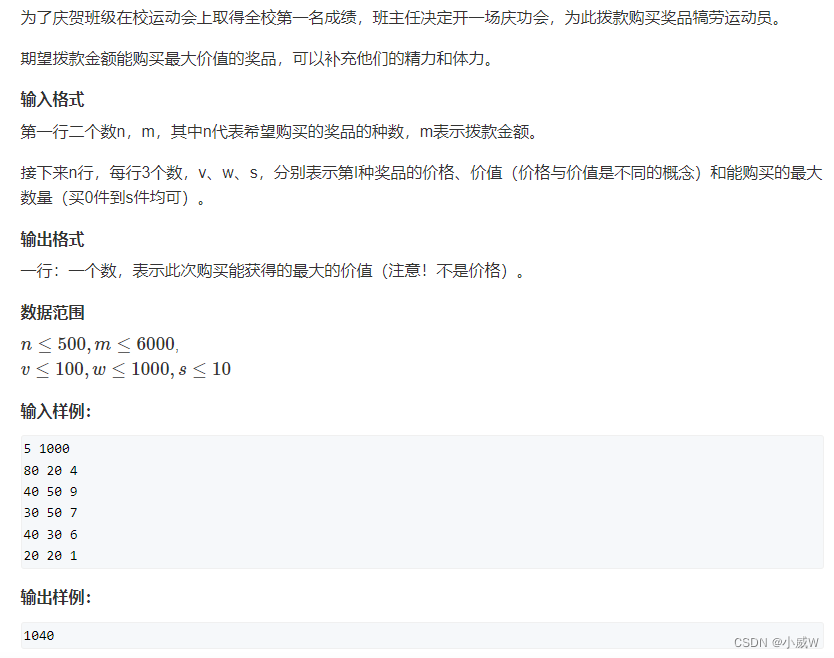
这个数据范围,转换成 01背包问题,不需要使用 二进制优化。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
int[] dp = new int[m + 1];
for (int i = 0; i < n; ++i) { // 枚举每一组
int v = scanner.nextInt(), w = scanner.nextInt(), s = scanner.nextInt();
for (int j = m; j >= v; --j) { // 枚举容量
for (int k = 1; k <= s && k * v <= j; ++k) { // 枚举每一组的物品
dp[j] = Math.max(dp[j], dp[j - k * v] + k * w);
}
}
}
System.out.println(dp[m]);
}
}
7. 混合背包问题(01 + 完全 + 多重 背包)
https://www.acwing.com/problem/content/7/

在最外侧枚举每一种物品,里层循环根据物品的种类套用不同的背包模板即可。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
int[] dp = new int[m + 1];
for (int i = 0; i < n; ++i) { // 枚举每一种物品
int v = scanner.nextInt(), w = scanner.nextInt(), s = scanner.nextInt();
if (s == -1) { // 01背包
for (int j = m; j >= v; --j) dp[j] = Math.max(dp[j], dp[j - v] + w);
} else if (s == 0) { // 完全背包
for (int j = v; j <= m; ++j) dp[j] = Math.max(dp[j], dp[j - v] + w);
} else { // 分组背包
for (int j = m; j >= v; --j) {
for (int k = 1; k <= s && j >= k * v; ++k) {
dp[j] = Math.max(dp[j], dp[j - k * v] + k * w);
}
}
}
}
System.out.println(dp[m]);
}
}
8. 二维费用的背包问题(标准模板题)
https://www.acwing.com/activity/content/problem/content/1277/

import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), v = sin.nextInt(), m = sin.nextInt();
int[][] dp = new int[v + 1][m + 1];
for (int i = 0; i < n; ++i) { // 枚举物品
int vv = sin.nextInt(), mm = sin.nextInt(), w = sin.nextInt();
// 倒序枚举两种容量
for (int j = v; j >= vv; --j) {
for (int k = m; k >= mm; --k) {
dp[j][k] = Math.max(dp[j][k], dp[j - vv][k - mm] + w);
}
}
}
System.out.println(dp[v][m]);
}
}
1020. 潜水员(二维费用的背包问题,装到满足条件的最少重量)🐂 好题!
https://www.acwing.com/problem/content/1022/

数据范围:1≤m≤21, 1≤n≤79, 1≤k≤1000, 1≤ai≤21, 1≤bi≤79, 1≤ci≤800
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int m = sin.nextInt(), n = sin.nextInt();
int k = sin.nextInt();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; ++i) Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
dp[0][0] = 0;
for (int i = 0; i < k; ++i) {
int a = sin.nextInt(), b = sin.nextInt(), c = sin.nextInt();
for (int j = m; j >= 0; --j) {
for (int q = n; q >= 0; --q) {
// 由于是求满足要求而不是正好的,所以需要做下面的处理。
// 即 a 和 b 可以被浪费
if (j >= a && q >= b) dp[j][q] = Math.min(dp[j][q], dp[j - a][q - b] + c);
else if (j >= a) dp[j][q] = Math.min(dp[j][q], dp[j - a][0] + c);
else if (q >= b) dp[j][q] = Math.min(dp[j][q], dp[0][q - b] + c);
else dp[j][q] = Math.min(dp[j][q], c);
}
}
}
System.out.println(dp[m][n]);
}
}
代码优化
那 4 个 if - else 可以通过一个求 Math.max() 缩减到 1 行代码。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int m = sin.nextInt(), n = sin.nextInt();
int k = sin.nextInt();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; ++i) Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
dp[0][0] = 0;
for (int i = 0; i < k; ++i) {
int a = sin.nextInt(), b = sin.nextInt(), c = sin.nextInt();
for (int j = m; j >= 0; --j) {
for (int q = n; q >= 0; --q) {
// 由于是求满足要求而不是正好的,所以需要做下面的处理。
// 即 a 和 b 可以被浪费
dp[j][q] = Math.min(dp[j][q], dp[Math.max(j - a, 0)][Math.max(q - b, 0)] + c);
}
}
}
System.out.println(dp[m][n]);
}
}
1013. 机器分配⭐(转换成分组背包问题 + 记录转移路径)
https://www.acwing.com/activity/content/problem/content/1279/

简单思路可以想起来:将问题转换成分组背包问题,每个公司是一个组,每组中的物品是给该公司分配几台机器。
这样可以求出来最大盈利,代码如下:
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
int[][] g = new int[n + 1][m + 1];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
g[i][j] = sin.nextInt();
}
}
int[] dp = new int[m + 1];
for (int i = 0; i < n; ++i) { // 枚举每一组(每个公司)
for (int j = m; j >= 0; j--) { // 枚举背包容量
for (int k = 1; k <= j; ++k) { // 枚举每一组的物品(每个公司分配几个)
dp[j] = Math.max(dp[j], dp[j - k] + g[i][k - 1]);
}
}
}
System.out.println(dp[m]);
}
}
但是怎么记下当时的具体分配方案呢?⭐⭐⭐
一个朴素的想法是,当 dp[j] 更新的时候,就记下此时的 k,但是 不对!
正确的做法如下:
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
int[][] g = new int[n + 1][m + 1];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
g[i][j] = sin.nextInt();
}
}
// 求最大盈利
int[][] dp = new int[n + 1][m + 1]; // dp[i][j] 表示考虑0~i组时,容量j的最大价值
for (int i = 1; i <= n; ++i) { // 枚举每一组(每个公司)
for (int j = m; j >= 1; j--) { // 枚举背包容量
for (int k = 0; k <= j; ++k) { // 枚举每一组的物品(每个公司分配几个)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k] + g[i][k]);
}
}
}
System.out.println(dp[n][m]);
// 求分配方案
int[] way = new int[n + 1];
int j = m;
for (int i = n; i >= 1; --i) { // 枚举每一组
for (int k = 0; k <= j; ++k) { // 枚举每一组用了几个
if (dp[i - 1][j - k] + g[i][k] == dp[i][j]) {
way[i] = k;
j -= k;
break;
}
}
}
for (int i = 1; i <= n; ++i) System.out.println(i + " " + way[i]);
}
}
即通过 dp 数组,反向找到 dp 转移的路径,就可以得到具体的分配方案。
426. 开心的金明(转换成01背包)
https://www.acwing.com/problem/content/428/

数据范围
1≤N<30000 , 1≤m<25 , 0≤v≤10000 , 1≤p≤5
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
int[] dp = new int[n + 1];
for (int x = 2; x <= m + 1; ++x) { // 枚举每个物品
int v = sin.nextInt(), p = sin.nextInt();
for (int j = n; j >= v; --j) {
dp[j] = Math.max(dp[j], dp[j - v] + v * p);
}
}
System.out.println(dp[n]);
}
}
10. 有依赖的背包问题⭐⭐⭐⭐⭐🚹🐂(树形DP + 分组背包)好题!
https://www.acwing.com/problem/content/10/
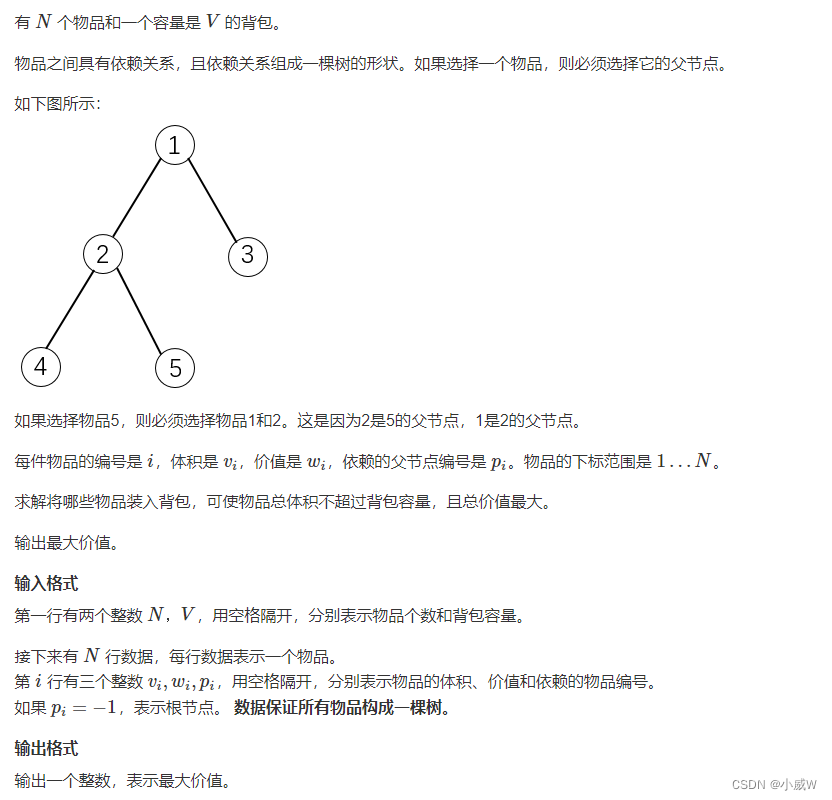
目标:f(u, j) —— 表示以 u 为根节点,在 j 的体积下,可以选出的最大价值是多少。
对于这道题目使用树形DP的框架,节点的每个儿子是一个组。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
static List<Integer>[] g;
static int[] v, w;
static int[][] dp; // dp[x][j] 表示以x为根节点使用体积j时的最大价值
static int n, m; // 物品个数 和 背包容量
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
n = sin.nextInt();
m = sin.nextInt();
g = new ArrayList[n + 1];
v = new int[n + 1];
w = new int[n + 1];
int root = 0;
dp = new int[n + 1][m + 1];
Arrays.setAll(g, e -> new ArrayList<>());
for (int i = 1; i <= n; ++i) {
v[i] = sin.nextInt();
w[i] = sin.nextInt();
int p = sin.nextInt();
if (p != -1) g[p].add(i);
else root = i;
}
dfs(root); // 树形dp过程
System.out.println(dp[root][m]);
}
static void dfs(int x) {
// 枚举 x 的每一个儿子 y (其实就是枚举每个组)
for (int y: g[x]) {
dfs(y);
// 分组背包
for (int j = m - v[x]; j >= 0; --j) { // 枚举体积 (此时留下了给物品 x 的体积)
for (int k = 0; k <= j; ++k) { // 枚举这个组里的儿子使用多少体积
dp[x][j] = Math.max(dp[x][j], dp[x][j - k] + dp[y][k]);
}
}
}
// 将物品 x 加进入
for (int j = m; j >= v[x]; --j) dp[x][j] = dp[x][j - v[x]] + w[x]; // 装得下 x
for (int j = 0; j < v[x]; ++j) dp[x][j] = 0; // 装不下 x
}
}
11. 背包问题求方案数
https://www.acwing.com/activity/content/problem/content/1282/

这道题目的风格有点像:673. 最长递增子序列的个数,我常用的解决方法就是开两个数组分别记录最大价值和对应的方案数。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt(), mxV = 0;
final int MOD = (int)1e9 + 7;
int[] dp = new int[m + 1], cnt = new int[m + 1]; // dp记录最大价值,cnt记录对应的方案数
cnt[0] = 1;
for (int i = 0; i < n; ++i) { // 枚举物品
int v = sin.nextInt(), w = sin.nextInt();
for (int j = m; j >= v; --j) { // 枚举容量
int newV = dp[j - v] + w;
if (newV > dp[j]) {
dp[j] = newV;
cnt[j] = cnt[j - v];
} else if (newV == dp[j]) cnt[j] = (cnt[j] + cnt[j - v]) % MOD;
mxV = Math.max(dp[j], mxV);
}
}
int res = 0;
for (int i = 0; i <= m; ++i) {
if (dp[i] == mxV) res = (res + cnt[i]) % MOD;
}
System.out.println(res);
}
}
12. 背包问题求具体方案()🐂好题!
https://www.acwing.com/activity/content/problem/content/1283/
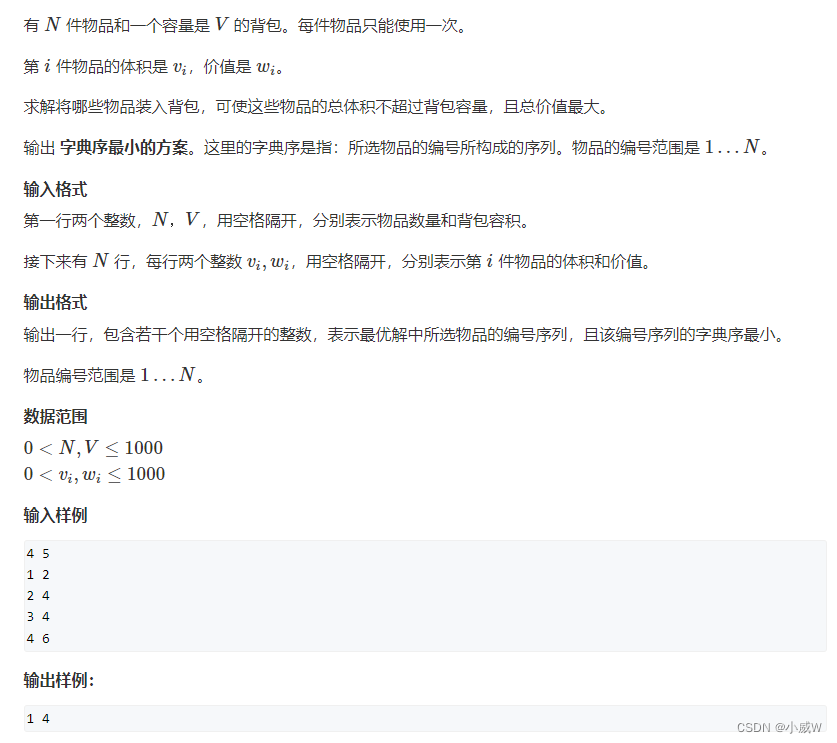
这个规定 字典序最小,其实是为了出题人方便检查答案是否正确。
因为下面求答案的时候要从前往后枚举物品,因此前面的背包dp过程要从后往前枚举物品。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
// 这种需要将具体方案求出的题目,大概都要使用二维的dp数组
int[][] dp = new int[n + 2][m + 1];
int[] v = new int[n + 1], w = new int[n + 1];
for (int i = 1; i <= n; ++i) {
v[i] = sin.nextInt();
w[i] = sin.nextInt();
}
// 倒着加物品(因为要求字典序最小的方案,后枚举编号小的可以将编号大的覆盖)
// 因为下面求答案是要从前往后枚举,所以这里要从后往前枚举
for (int i = n; i >= 1; --i) {
for (int j = m; j >= 0; --j) { // TODO:很奇怪,这里j 0~m 和 m~0 的顺序都可以 (或许是因为 dp 数组是两维的)
dp[i][j] = dp[i + 1][j];
if (j >= v[i]) dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - v[i]] + w[i]);
}
}
int j = m;
// 从前往后枚举,能取就取出来,这样字典序是最小的
for (int i = 1; i <= n; ++i) {
if (j >= v[i] && dp[i][j] == dp[i + 1][j - v[i]] + w[i]) {
System.out.print(i + " ");
j -= v[i];
}
}
}
}
要厘清几个点:
- 因为最后推答案的时候需要从前往后(为了得到字典序最小的),因此前面推dp的时候要从后往前。
- 二维dp数组的话,容量 j 的枚举顺序是无所谓的。
734. 能量石(贪心 + dp)⭐🐂(重点学习贪心思维!比较相邻两个元素)
https://www.acwing.com/problem/content/736/

贪心:
对于 i 和 i + 1
先吃 i 的话,
e
i
+
e
i
+
1
−
s
i
∗
l
i
+
1
e_i + e_{i+1} - s_i*l_{i+1}
ei+ei+1−si∗li+1
先吃 i + 1 的话,
e
i
+
e
i
+
1
−
s
i
+
1
∗
l
i
e_i + e_{i+1} - s_{i+1}*l_{i}
ei+ei+1−si+1∗li
为了让先吃 i 由于 先吃 i + 1,需要有 s i ∗ l i + 1 < s i + 1 ∗ l i s_i*l_{i+1}<s_{i+1}*l_{i} si∗li+1<si+1∗li,由此得出自定义排序的代码为:
Arrays.sort(stones, (a, b) -> {
return a[0] * b[2] - b[0] * a[2];
});
排序之后,就可以按排序之后的顺序依次尝试吃这些石头。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int t = sin.nextInt(), x = 1;
while (t-- != 0) {
int n = sin.nextInt(), m = 0;
int[][] stones = new int[n][3]; // s,e,l
for (int i = 0; i < n; ++i) {
stones[i][0] = sin.nextInt();
stones[i][1] = sin.nextInt();
stones[i][2] = sin.nextInt();
m += stones[i][0];
}
Arrays.sort(stones, (a, b) -> {
return a[0] * b[2] - b[0] * a[2];
});
int[][] dp = new int[n + 1][m + 1];
// 按排序后的顺序尝试吃这些石头
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
dp[i][j] = dp[i - 1][j]; // 至少和之前一样
if (j >= stones[i - 1][0]) { // 如果时间够吃
int s = stones[i - 1][0], e = stones[i - 1][1], l = stones[i - 1][2];
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - s] + Math.max(0, e - l * (j - s)));
}
}
}
System.out.printf("Case #%d: %d\n", x++, Arrays.stream(dp[n]).max().getAsInt());
}
}
}
487. 金明的预算方案(有依赖的状态压缩分组背包DP问题)⭐🐂(好题!)
https://www.acwing.com/activity/content/problem/content/1285/

每个主件及其跟随的副件,可以作为一组。
其中主件必须被选择,跟随的副件的选择情况可以使用状态压缩来做。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
int n = sin.nextInt(), m = sin.nextInt();
int[][] master = new int[n + 1][2];
List<int[]>[] servant = new ArrayList[n + 1];
Arrays.setAll(servant, e -> new ArrayList<int[]>());
// 处理输入,每个物品的价值是 v*p
for (int i = 1; i <= m; ++i) {
int v = sin.nextInt(), p = sin.nextInt(), q = sin.nextInt();
if (q == 0) { // 主件
master[i] = new int[]{v, v * p};
} else { // 附件
servant[q].add(new int[]{v, v * p});
}
}
int[] dp = new int[n + 1];
for (int i = 1; i <= m; ++i) { // 处理每一组物品
for (int j = n; j >= 0; --j) { // 枚举钱数
// 枚举副件的选取状态
for (int mask = 0; mask < 1 << servant[i].size(); ++mask) {
// 获取主件,作为v和w的初始值(因为主件是一定要被选的)
int v = master[i][0], w = master[i][1];
// 枚举被选择的副件 状态集合
for (int k = 0; k < servant[i].size(); ++k) {
if ((mask >> k & 1) == 1) { // 如果第k个副件被选择了
v += servant[i].get(k)[0];
w += servant[i].get(k)[1];
}
}
if (j >= v) dp[j] = Math.max(dp[j], dp[j - v] + w);
}
}
}
System.out.println(dp[n]);
}
}
相关链接
【算法】01背包和完全背包
【算法基础:动态规划】5.1 背包问题






![P4053 [JSOI2007] 建筑抢修(贪心)(内附封面)](https://img-blog.csdnimg.cn/0c46654e82ae4450954a1edafd1095a0.png)