解题思路来自这个博客：@简单^不简单
https://blog.csdn.net/younger_china/article/details/126376374

描述

花花有一个很珍贵的数字串，但是它太长了，没有办法保留下来，所以她想截取其中一段保存下来，但是她希望截取下来的这一段数对1000000007取模之后等于Ai，她想知道有多少种截取方案。数字串S中截取一段是指S[L], S[L+1], …, S[R]连起来所形成的十进制数，其中L和R满足1≤L≤R≤|S|。例如S=“1023456789”，S(1,2)=10，S(2,4)=23，S(2,10)=23456789。

输入描述

第一行一个数字串，长度不超过30000。

第二行一个数T，表示询问的数量。（T≤100）

接下来T行，每行一个非负整数Ai，表示询问有多少种截取方案使得其值模1000000007后等于Ai。（0≤Ai<1000000007）

输出描述

共T行，每行一个非负整数，表示方案数。

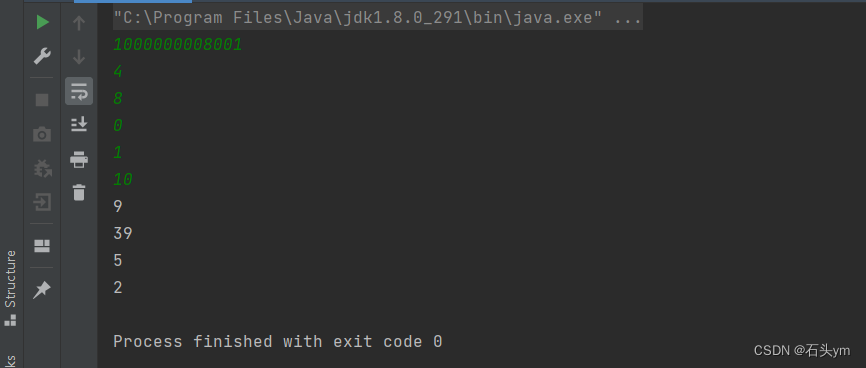
输入示例

1000000008001
4
8
0
1
10

输出示例

9
39
5
2

前置知识：

1.（a + b）％c =（（a％c）+（b％c））％c
2. （a * b）％c =（（a％c）*（b％c））％c
3.（a – b）％c =（（a％c）–（b％c））％c

代码

import java.util.Scanner;
public class Main {
    static int tempMod = 1000000007;
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        String bd = in.nextLine();
        int n = in.nextInt();
        int[] nums = new int[n];
        for(int i = 0; i < n; i++) {
            nums[i] = in.nextInt();
        }
        for(int i = 0; i < n; i++) {
            System.out.println(find(bd,nums[i]));
        }
    }
    public static int find(String bd, int remainder) {
        int count = 0;
        for(int i = 0; i<=bd.length()-1;i++) {
        //第一层for循环表示从第i个值开始
            long remin = bd.charAt(i) - '0';
            //这里if语句判断表示只取一个值，做判断
            if(remin == remainder) {
                count++;
                if(i > 0){
                //这里的for循环表示当i左边还有数的时候，判断是否有0，有连续的n个0，就count自增n次，一定要连续，否则退出
                    for(int k = i-1; k >= 0;k--) {
                        if(bd.charAt(k) == '0') count++;
                        else break;
                    }
                }
            }
            if(remin != 0){
            //这里的for循环属于第二层for循环，作为判断截取数以坐标i开头，坐标j结尾的非个位数是否符合要求
            //注意，这里第二层判断的时候，开头的数坐标i不能等于0，不然没有意义，所以做了if判断
                for(int j = i+1;j <bd.length();j++) {
                    remin = ((remin * 10) % tempMod + (bd.charAt(j)-'0')) % tempMod;
                    if(remin == remainder){
                        count++;
                        if(i > 0){
                        //同样，当该数符合要求的时候，前面若还有数，判断是否有0，有连续的n个0，就count自增n次，一定要连续，否则退出
                            for(int k = i-1; k >= 0;k--) {
                                if(bd.charAt(k) == '0') count++;
                                else break;
                            }
                        }
                    }
                }
            }

        }
        return count;
    }
}