跳表–skiplist

skiplist的概念

skiplist本质上也是一种查找结构，用于解决算法中的查找问题。skiplist，顾名思义，首先它是一个list。它是在有序链表的基础上发展起来的。有序链表的的查找数据的时间复杂度是O(n);

skilplist相对于list做出了优化，类似于二分查找，查找的时间复杂度是log(n);

假如我们每相邻两个节点升高一层，增加一个指针，让指针指向下下个节点。这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了，需要比较的节点数大概只有原来的一半。
以此类推，在第二层新产生的链表上，继续为每相邻的两个节点升高一层，增加一
个指针，从而产生第三层链表。
这样查找过程就非常类似二分查找，使得查找的时间复杂度可以降低到O(log n)。但是在插入或者删除一个节点时，就打乱了上下的层次关系。**为了维持2：1的对应关系，需要调整整个链表，时间复杂度就又变成了O(n)。 **

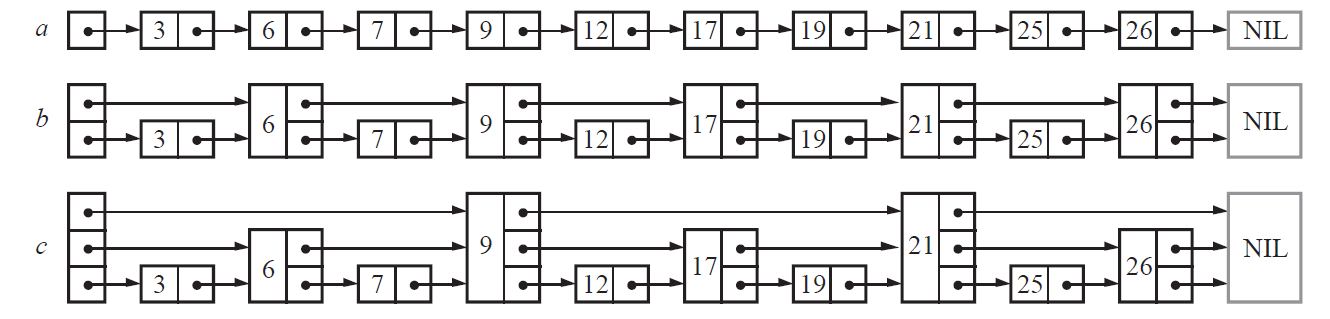
在设计跳表时，设计师对Skiplist作出了大胆的优化。不再严格要求对于的比例关系，而是插入一个节点时，随机赋予一个层数。当然这里的层数是在一个范围内的随机值

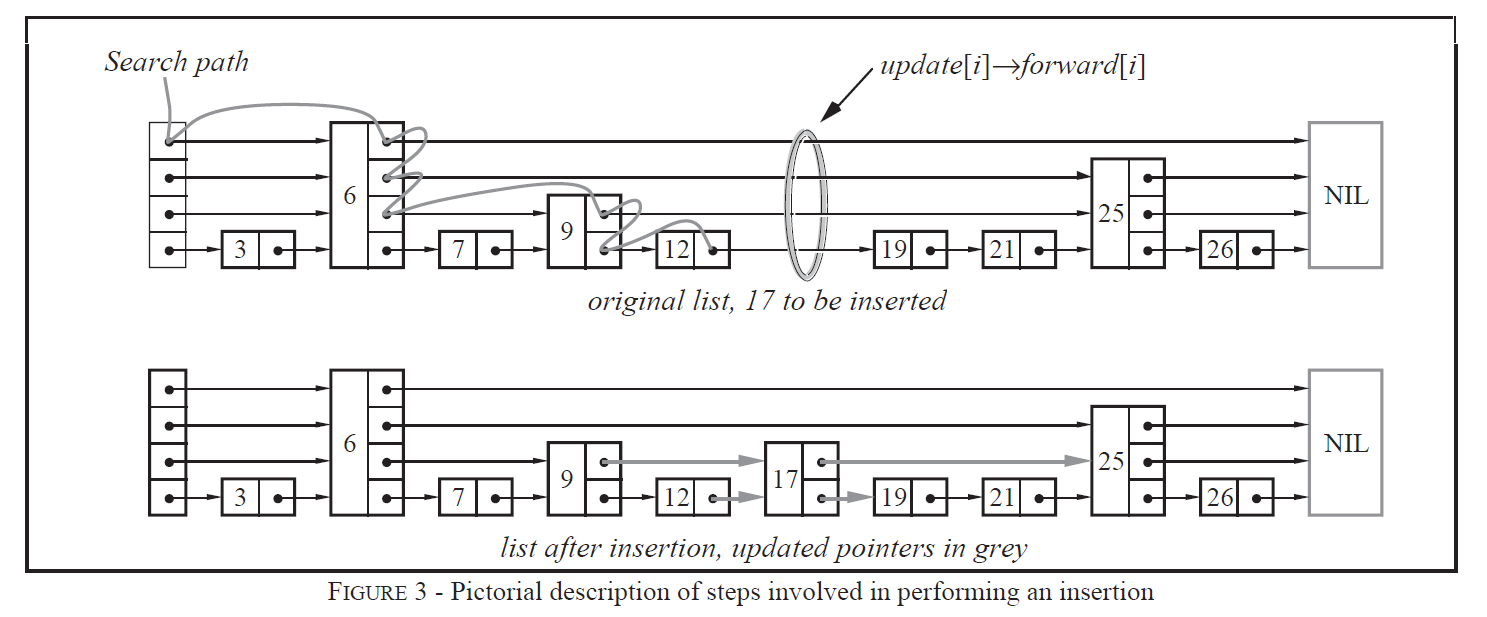
skilplist的原理

层数的随机值

最大层数maxLevel
p：增加一层的概率

在Redis中的skiplist，maxlevel取值为32，p为1/4

数学原理

P表示新增加一层的概率，节点层数至少为1。而大于1的节点层数，满足一个概率分布。

节点层数恰好等于1的概率为1-p。
节点层数大于等于2的概率为p，而节点层数恰好等于2的概率为p(1-p)。
节点层数大于等于3的概率为p^{2，而节点层数恰好等于3的概率为p}2*(1-p) 。
节点层数大于等于4的概率为p^{3，而节点层数恰好等于4的概率为p}3*(1-p) 。
…

通过错位相减，可以得到平均的层数：

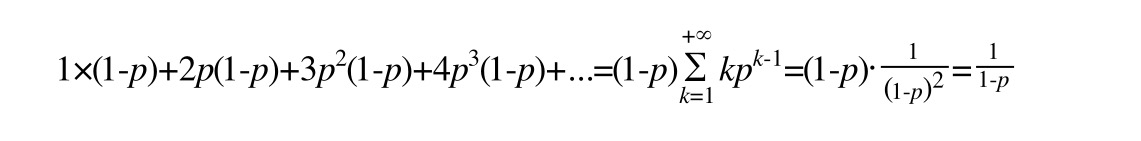
skilplist的实现

跳表OJ：

https://leetcode.cn/problems/design-skiplist/

随机值函数

因为插入一个节点时，层数是随机的，所以需要设计一个随机值函数。

C++的写法

int RandomLevel()
{
	static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());
	static std::uniform_real_distribution<double> distribution(0.0, 1.0);
	size_t level = 1;
    // _p是增加一层的概率，_maxLevel是最大的层数
	while (distribution(generator) <= _p && level < _maxLevel)
	{
		++level;
	}
	return level;
}

C语言的写法

int RandomLevel()
{
	size_t level = 1;
	// RAND_MAX是一个宏，即最大的随机值
	while (rand() < RADN_MAX *_p && level < _maxLevel)
	{
		level++;
	}
	return level;
}

跳表节点

template<class K,class V>
struct skiplistnode{
    //存储的键值对
    K _key;
    V _value;
    vector<skiplistnode*> _nextV;
    //创建一个节点
    skiplistnode(K key,V value,int level)
    :_key(key),_value(value),_nextV(level,nullptr)
    {}
};

跳表框架

跳表的主要功能有增加元素，删除元素，操作元素等。跳表是一个Key-Value的查找结构，所以需要实现一个模板。

template <class K, class V>
class skiplist
{
    typedef skiplistnode<K, V> Node;
public:
    // 构造函数
    skiplist()
    {
        srand(time(0));
        _head = new Node(K(), V(), 1);
    }
    
    // 查找函数
    pair<V, bool> search(K target)
    {}
    
	//查找前置结点，返回一个vector，包含target每一层的前置节点
    vector<Node *> Findprev(K target)
    {}
    
    
	//添加元素函数
    void add(K key, V value)
    {}
    
	//删除函数
    bool erase(K target)
    {}
    
    
	//打印链表，每一层为一个链表
    void print()
    {}
    
	//随机值生成函数
    int RandomLevel()
    {}
private:
    double _p = 0.25;
    int _maxLevel = 32;
    Node *_head;
};

查找函数

查找关键字Key，返回对应的值。

// 查找函数
pair<V, bool> search(K target)
{
    Node *cur = _head;
    int level = _head->_nextV.size() - 1;
    while (level >= 0)
    {
        if (cur->_nextV[level] && target > cur->_nextV[level]->_key)
        {
            cur = cur->_nextV[level];
        }
        else if (cur->_nextV[level] == nullptr || target < cur->_nextV[level]->_key)
        {
            level--;
        }
        else
        {
            return make_pair(cur->_nextV[level]->_value, true);
        }
    }
    return make_pair(V(), false);
}

寻找前置节点

查找前置结点，返回一个vector，包含关键字target每一层的前置节点指针。

vector<Node *> Findprev(K target)
{
    int level = _head->_nextV.size() - 1;
    vector<Node *> prevnode(level + 1, _head);
    // 寻找前置节点
    Node *cur = _head;
    while (level >= 0)
    {
        if (cur->_nextV[level] && target > cur->_nextV[level]->_key)
        {
            cur = cur->_nextV[level];
        }
        else if (cur->_nextV[level] == nullptr || target <= cur->_nextV[level]->_key)
        {
            prevnode[level] = cur;
            level--;
        }
    }
    return prevnode;
}

添加元素

向链表这插入一个键值对

void add(K key, V value)
{
    // 先获取插入点的层数
    int newlevel = RandomLevel();
    Node *newnode = new Node(key, value, newlevel);
    // 创建一个数组用于获取每一层的前置结点
    vector<Node *> prev = Findprev(key);
    // 如果层数比哨兵位节点还要大，则需要调整大小哨兵位节点的层数
    if (newlevel > _head->_nextV.size())
    {
        _head->_nextV.resize(newlevel, nullptr);
        prev.resize(newlevel, _head);
    }

    // 连接结点
    for (size_t i = 0; i < newlevel; i++)
    {
        newnode->_nextV[i] = prev[i]->_nextV[i];
        prev[i]->_nextV[i] = newnode;
    }
}

删除元素

输入一个关键字Key，删除链表中第一个Key元素

bool erase(K target)
{
    vector<Node *> prev = Findprev(target);
    // 判断是否有当前的值，如果没有返回false
    if (prev[0]->_nextV[0] == nullptr || prev[0]->_nextV[0]->_value != target)
    {
        return false;
    }
    else
    {
        // 删除结点
        Node *del = prev[0]->_nextV[0];
        int level = del->_nextV.size();
        for (size_t i = 0; i < level; i++){
            prev[i]->_nextV[i] = del->_nextV[i];
        }
        delete del;
        // 判断是否要调整哨兵位的层数
        int n = _head->_nextV.size() - 1;
        while (n >= 0)
        {
            if (_head->_nextV[n]){
                break;
            }
            else{
                n--;
            }
        }
        _head->_nextV.resize(n + 1);
    }
    return true;
}

打印链表

打印链表，每一层为一个链表。

void print()
{
    int level = _head->_nextV.size() - 1;
    while (level--)
    {
        Node *cur = _head;
        while (cur)
        {
            if (cur->_nextV[level] != nullptr){
                cout << cur->_nextV[level]->_value << " ";
            }
            cur = cur->_nextV[level];
        }
        cout << endl;
    }
}

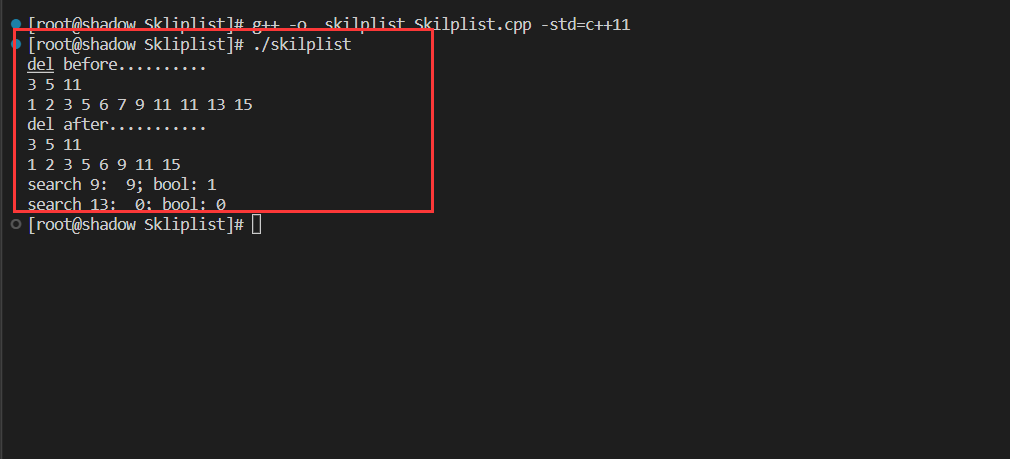
测试结果

#include"Skilplist.hpp"
#include<iostream>

int main(){
    skiplist<int,int> sklist;
    sklist.add(3,3);
    sklist.add(6,6);
    sklist.add(9,9);
    sklist.add(11,11);
    sklist.add(7,7);
    sklist.add(5,5);
    sklist.add(11,11);
    sklist.add(13,13);
    sklist.add(1,1);
    sklist.add(2,2);
    sklist.add(15,15);
    cout<<"del before.........."<<endl;
    sklist.print();
    sklist.erase(7);
    sklist.erase(8);
    sklist.erase(11);
    sklist.erase(13);
    cout<<"del after..........."<<endl;
    sklist.print();
    auto it1=sklist.search(9);
    cout<<"search 9:  "<<it1.first<<"; bool: "<<it1.second<<endl;
    auto it2=sklist.search(13);
    cout<<"search 13:  "<<it2.first<<"; bool: "<<it2.second<<endl;
    return 0;
}