标签：二叉树搜索 深度优先遍历 二叉树
思路一：递归实现反向中序遍历，并累加递归过程中的根的值
思路二：使用迭代，给每个根节点添加一个反向中序遍历的前驱节点。
原题链接：https://leetcode.cn/problems/convert-bst-to-greater-tree/description/?favorite=2cktkvj

1.题目如下：

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

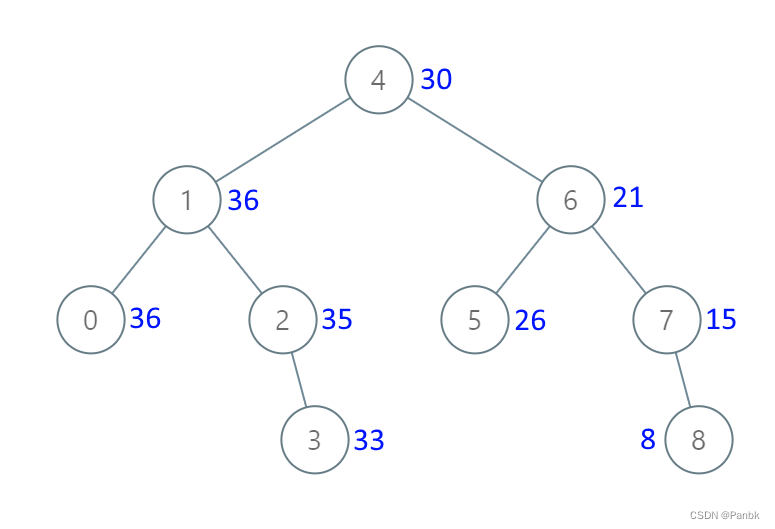
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

2.代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
//思路一：递归，反向中序
/*
    根节点的点数等于所有小于他的点数的和；所以用反向中序遍历
    
*/
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        if (root != nullptr) {
            //反向中序遍历，先向下递归right，再对本root->val赋值，最后遍历left
           convertBST(root->right);
           sum=sum+root->val;
           root->val=sum;
           convertBST(root->left);
        }
        return root;
    }

//思路二：采用Morris 遍历，通过迭代的方式
/*
    该方法就是：给每个节点都找到一个他右子树的前驱节点，然后从中序的最后一个节点往前比遍历，累加sum；
    相比于递归，该方法不需要栈。
*/
/*
    TreeNode* getSuccessor(TreeNode* node) {
        TreeNode* succ = node->right;
        while (succ->left != nullptr && succ->left != node) {
            succ = succ->left;
        }
        return succ;
    }

    TreeNode* convertBST(TreeNode* root) {
        int sum = 0;
        TreeNode* node = root;

        while (node != nullptr) {
            if (node->right == nullptr) {
                sum += node->val;
                node->val = sum;
                node = node->left;
            } else {
                TreeNode* succ = getSuccessor(node);
                if (succ->left == nullptr) {
                    succ->left = node;
                    node = node->right;
                } else {
                    succ->left = nullptr;
                    sum += node->val;
                    node->val = sum;
                    node = node->left;
                }
            }
        }

        return root;
    }
    */
};