概观
本文是有关 基于树的 回归和分类方法的。最近我们被客户要求撰写关于决策树的研究报告,包括一些图形和统计输出。
视频:从决策树到随机森林:R语言信用卡违约分析信贷数据实例
从决策树到随机森林:R语言信用卡违约分析信贷数据实例
,时长10:11
树方法简单易懂,但对于解释却非常有用,但就预测准确性而言,它们通常无法与最佳监督学习方法竞争。因此,我们还介绍了Bagging(自助法),随机森林和增强树。这些示例中的每一个都涉及产生多个树,然后将其合并以产生单个共识预测。我们看到,合并大量的树可以大大提高预测准确性,但代价是损失解释能力。
决策树可以应用于回归和分类问题。我们将首先考虑回归。
决策树基础:回归
我们从一个简单的例子开始:
我们预测棒球运动员的 Salary 。
结果将是一系列分裂规则。第一个分支会将数据分割 Years < 4.5 为左侧的分支,其余的为右侧。如果我们对此模型进行编码,我们会发现关系最终变得稍微复杂一些。
library(tree)
library(ISLR)
attach(Hitters)
# 删除NA数据
Hitters<- na.omit(Hitters)
# log转换Salary使其更正态分布
hist(Hitters$Salary)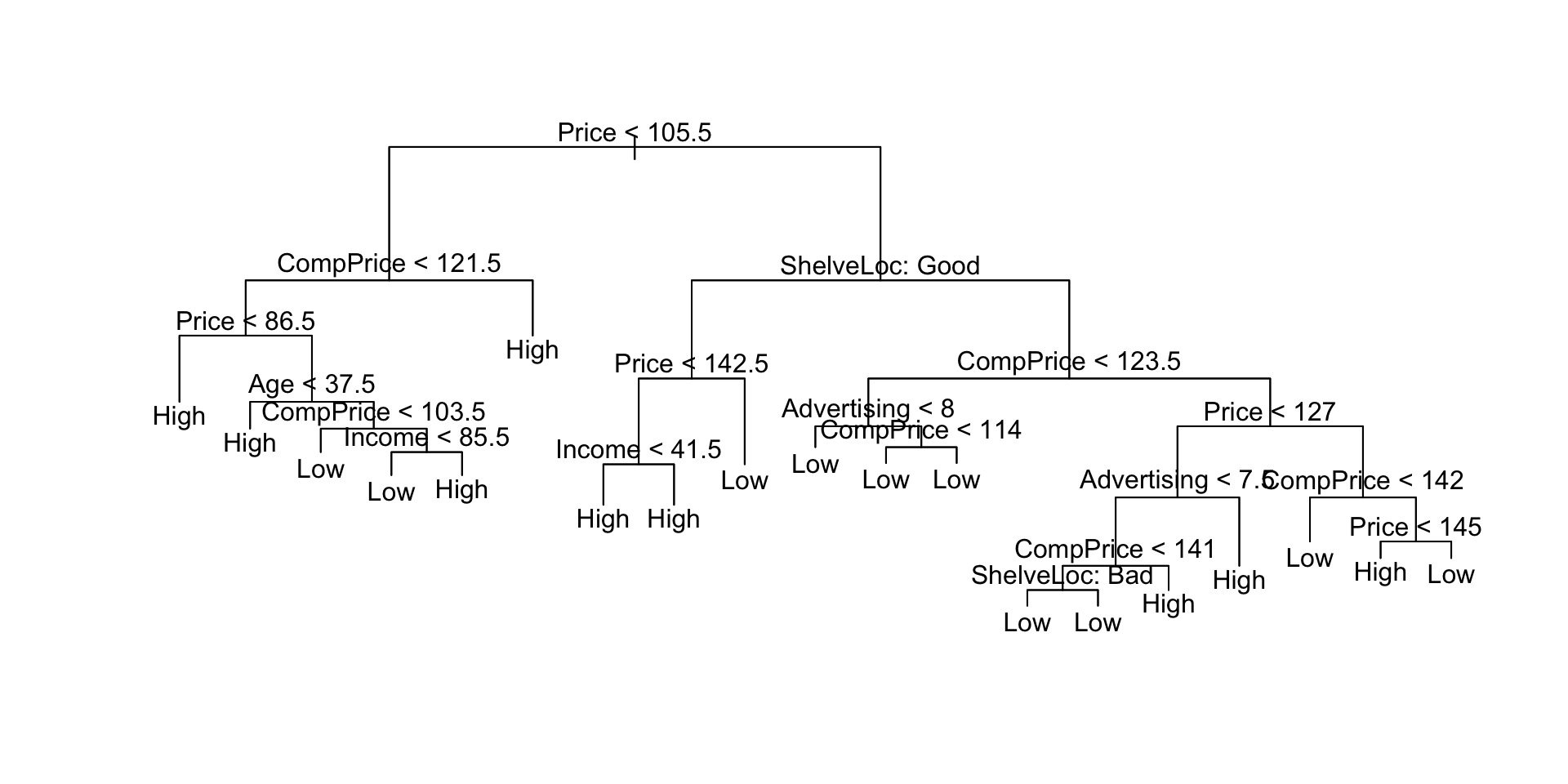
Hitters$Salary <- log(Hitters$Salary)
hist(Hitters$Salary)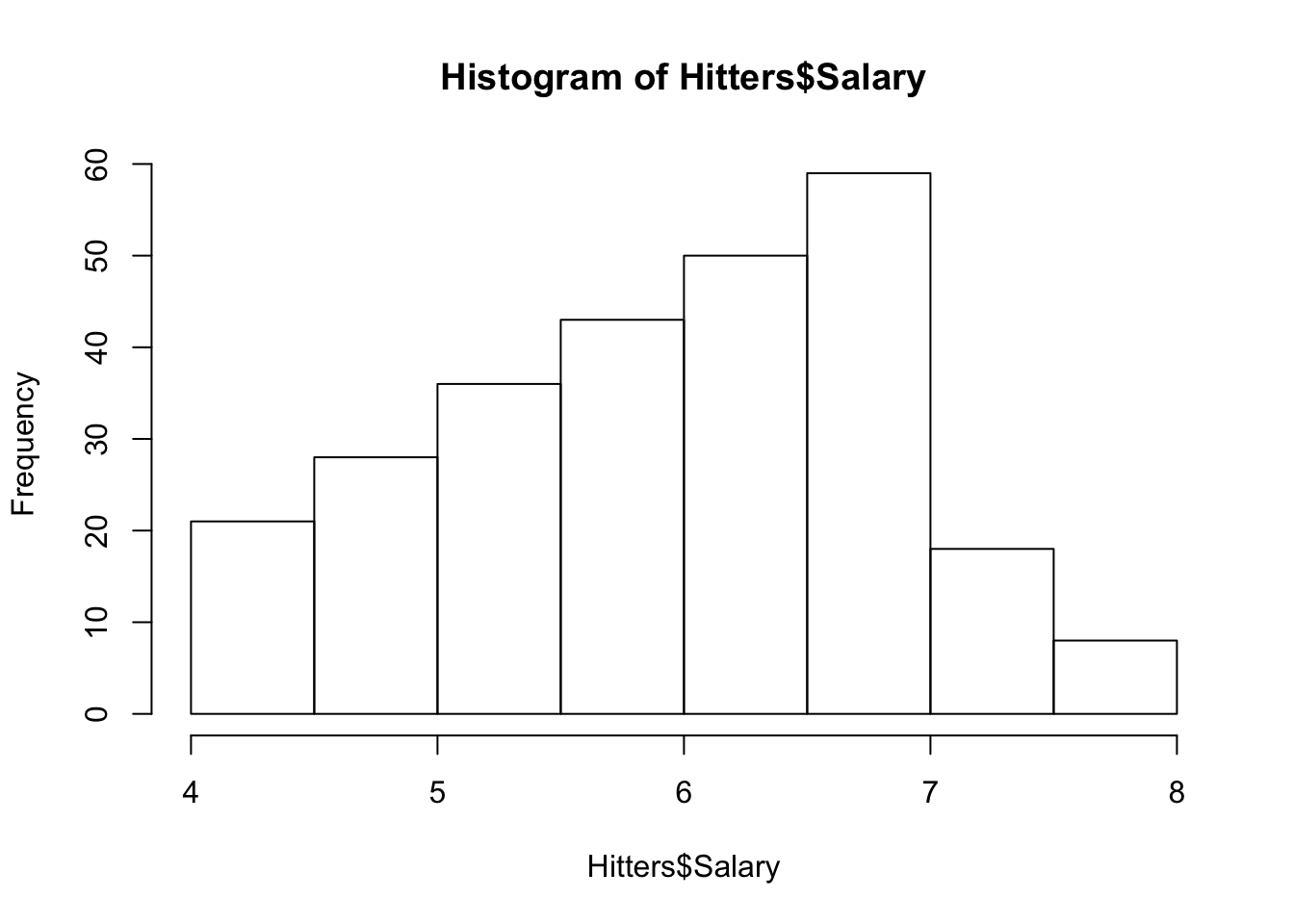
summary(tree.fit)##
## Regression tree:
## tree(formula = Salary ~ Hits + Years, data = Hitters)
## Number of terminal nodes: 8
## Residual mean deviance: 0.271 = 69.1 / 255
## Distribution of residuals:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -2.2400 -0.2980 -0.0365 0.0000 0.3230 2.1500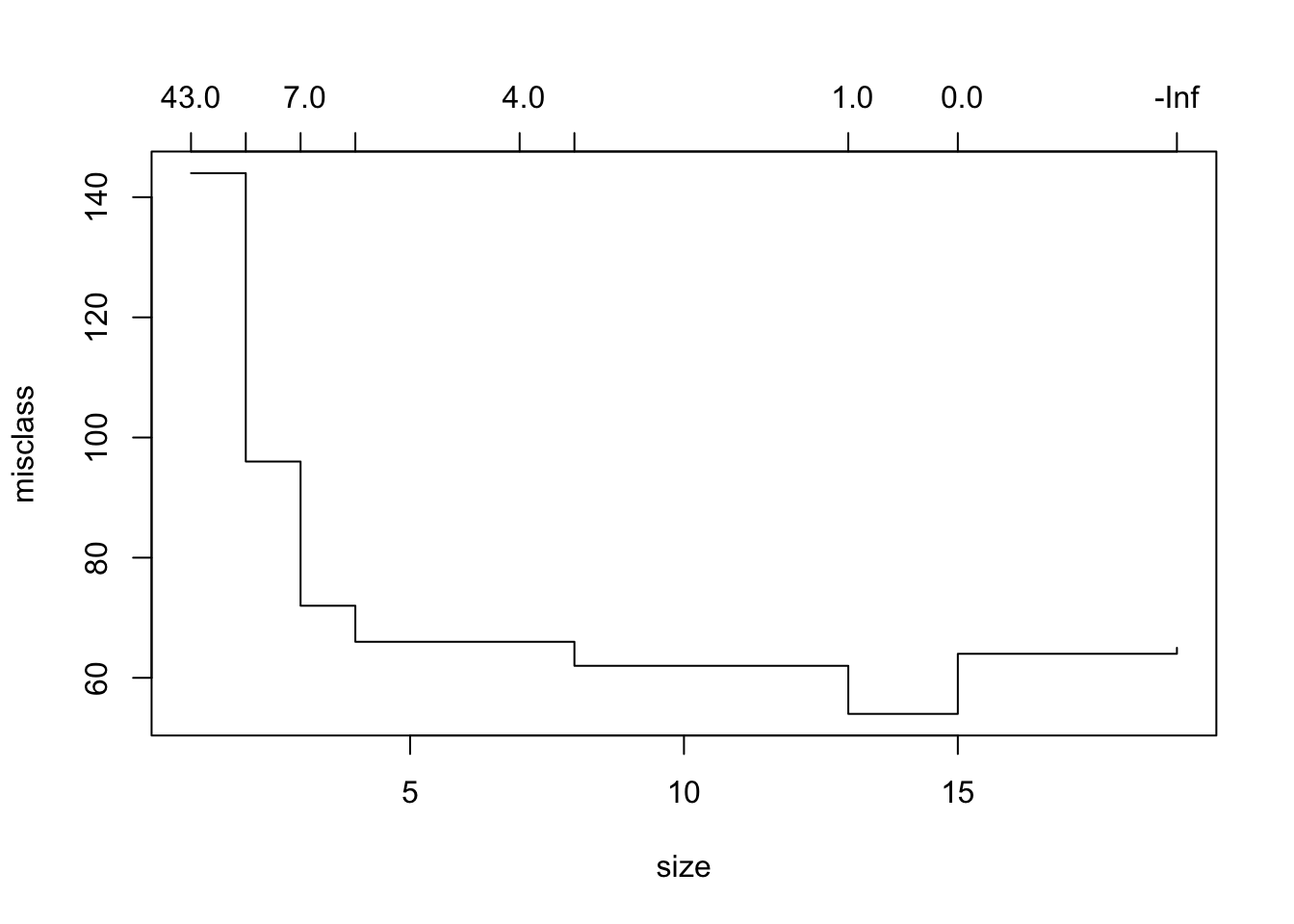
现在,我们讨论通过对特征空间进行分层来构建预测树。通常,有两个步骤。
-
找到最能分隔因变量的变量/拆分,从而产生最低的RSS。
-
将数据分为两个在第一个标识的节点上的叶子。
-
在每片叶子中,找到分隔结果的最佳变量/分割。
目标是找到最小化RSS的区域数。但是,考虑将每个可能的分区划分为J个区域在计算上是不可行的 。为此,我们采取了 自上而下的贪婪 的方法。它是自顶向下的,因为我们从所有观测值都属于一个区域的点开始。贪婪是因为在树构建过程的每个步骤中,都会在该特定步骤中选择最佳拆分,而不是向前看会在将来的某个步骤中生成更好树的拆分。
一旦创建了所有区域,我们将使用每个区域中训练观察的平均值预测给定测试观察的因变量。
剪枝
尽管上面的模型可以对训练数据产生良好的预测,但是基本的树方法可能会过度拟合数据,从而导致测试性能不佳。这是因为生成的树往往过于复杂。具有较少拆分的较小树通常以较小的偏差为代价,从而导致方差较低,易于解释且测试错误较低。实现此目的的一种可能方法是仅在每次拆分导致的RSS减少量超过某个(高)阈值时,才构建一棵树。
因此,更好的策略是生成一棵树,然后 修剪 回去以获得更好的子树。
成本复杂度剪枝算法-也称为最弱链接修剪为我们提供了解决此问题的方法。而不是考虑每个可能的子树,我们考虑由非负调整参数索引的树序列 alpha。
trees <- tree(Salary~., train)
plot(trees)
text(trees, pretty=0)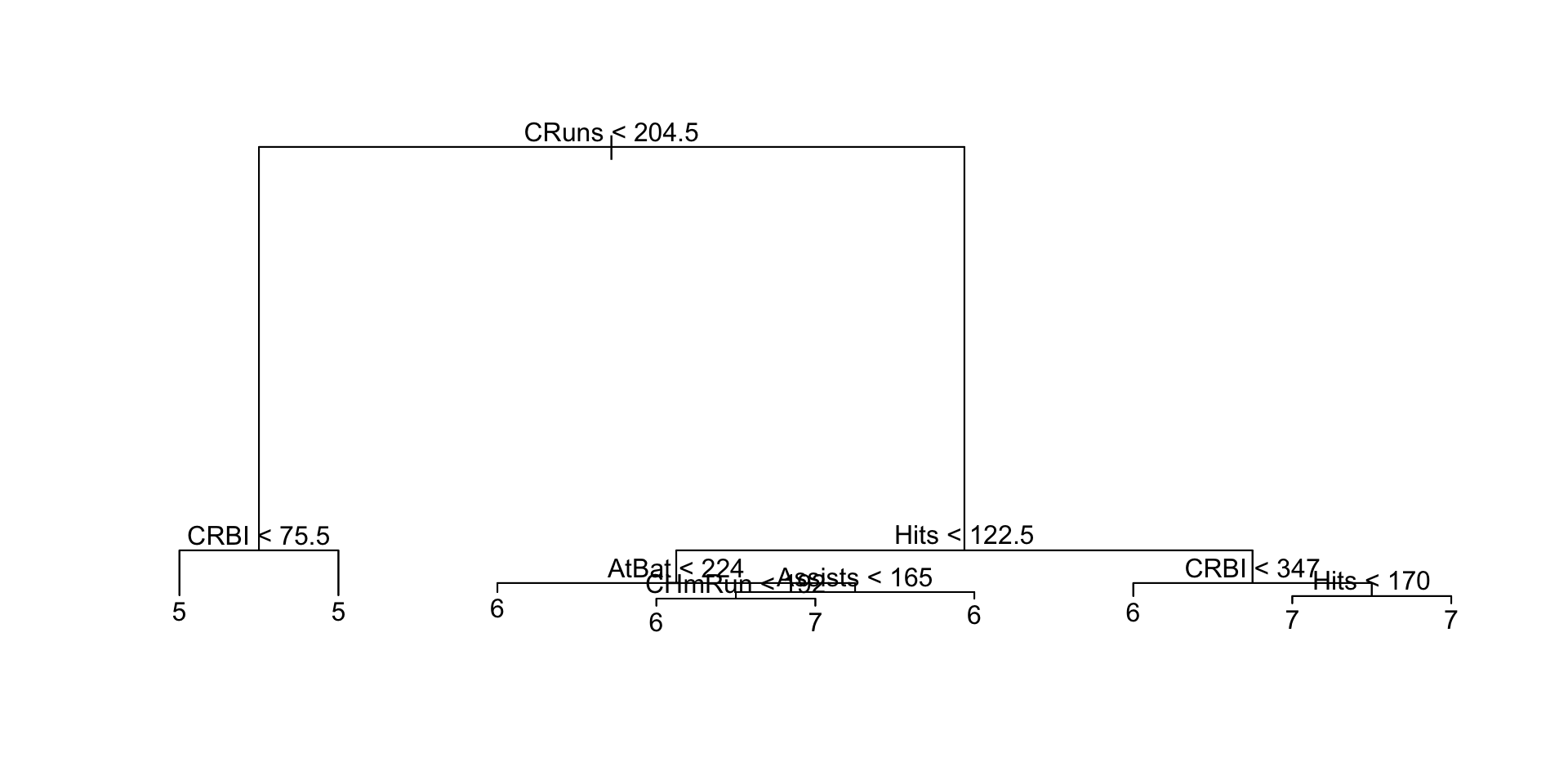
plot(cv.trees)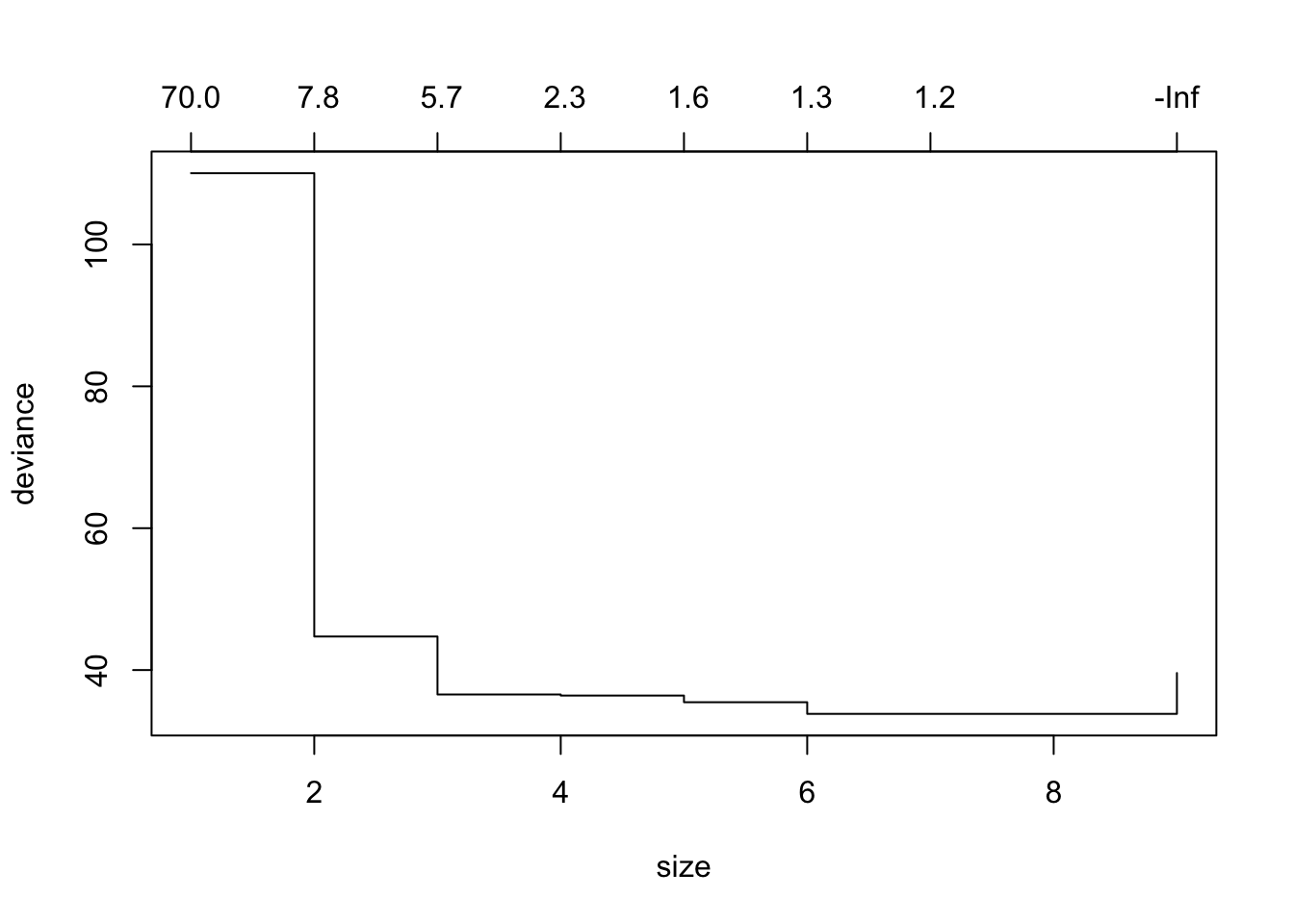
似乎第7棵树的偏差最小。然后我们可以剪枝树。但是,这并不能真正剪枝模型,因此我们可以选择较小的树来改善偏差状态。这大约是在第四个分支。
prune.trees <- prune.tree(trees, best=4)
plot(prune.trees)
text(prune.trees, pretty=0)
使用剪枝的树对测试集进行预测。
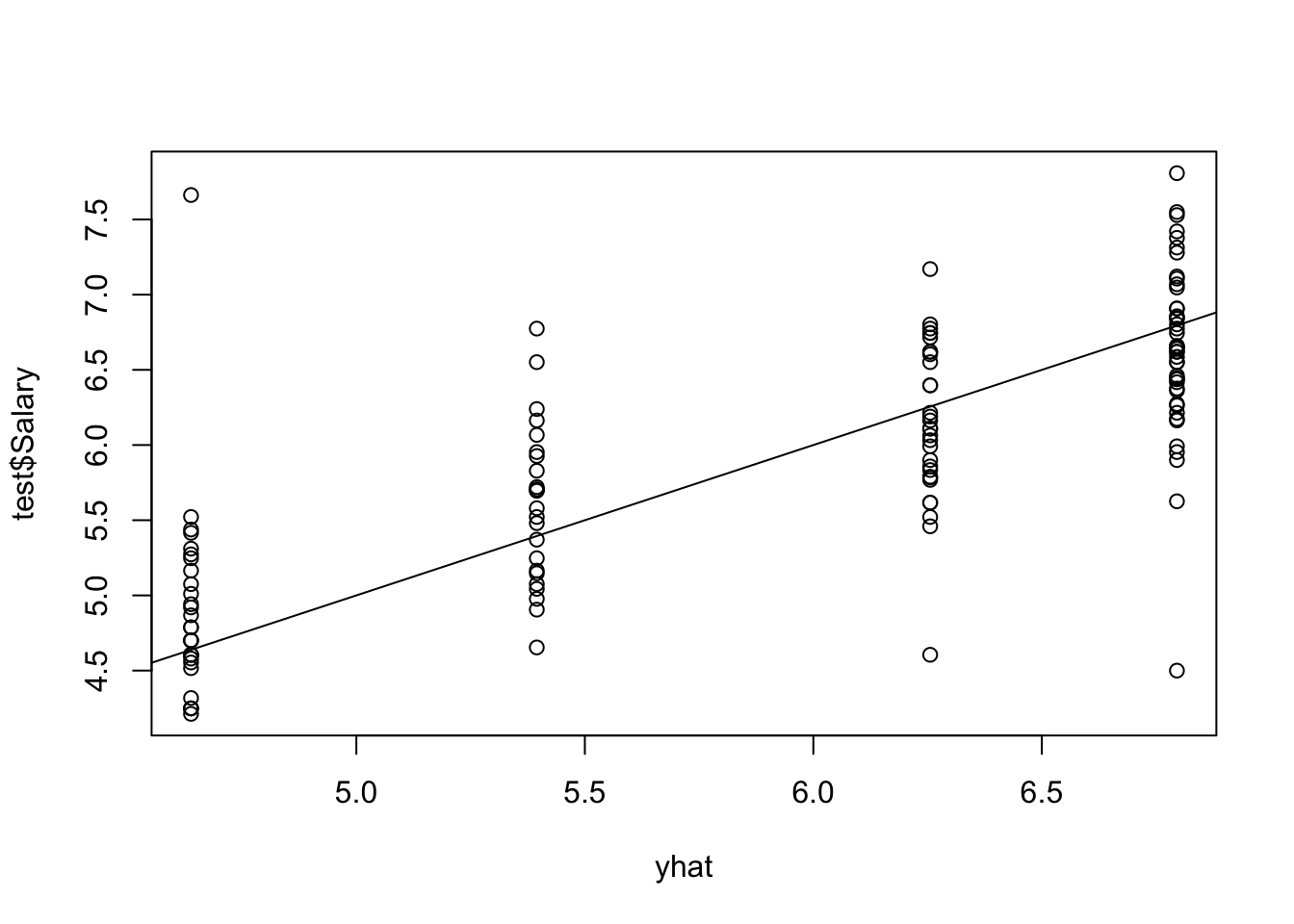
mean((yhat - test$Salary)^2)## [1] 0.3531分类树
分类树与回归树非常相似,不同之处在于分类树用于预测定性而不是定量。
为了增长分类树,我们使用相同的递归二进制拆分,但是现在RSS不能用作拆分标准。替代方法是使用 分类错误率。虽然很直观,但事实证明,此方法对于树木生长不够敏感。
实际上,另外两种方法是可取的,尽管它们在数值上非常相似:
Gini index_是K个 类之间总方差的度量 。
如果给定类别中的训练观测值的比例都接近零或一,则__cross-entropy_的值将接近零。
修剪树时,首选这两种方法,但如果以最终修剪模型的预测精度为目标,则规则分类错误率是优选的。
为了证明这一点,我们将使用 Heart 数据集。这些数据包含AHD 303名胸痛患者的二进制结果变量 。结果被编码为 Yes 或 No 存在心脏病。
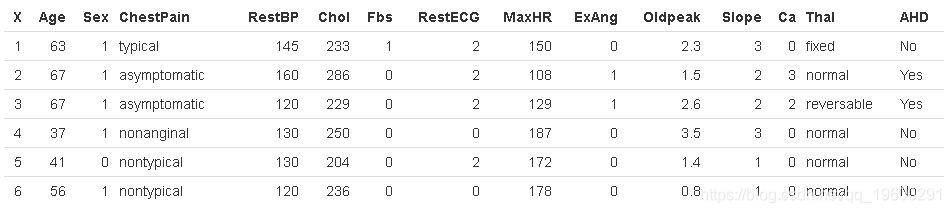
dim(Heart)
[1] 303 15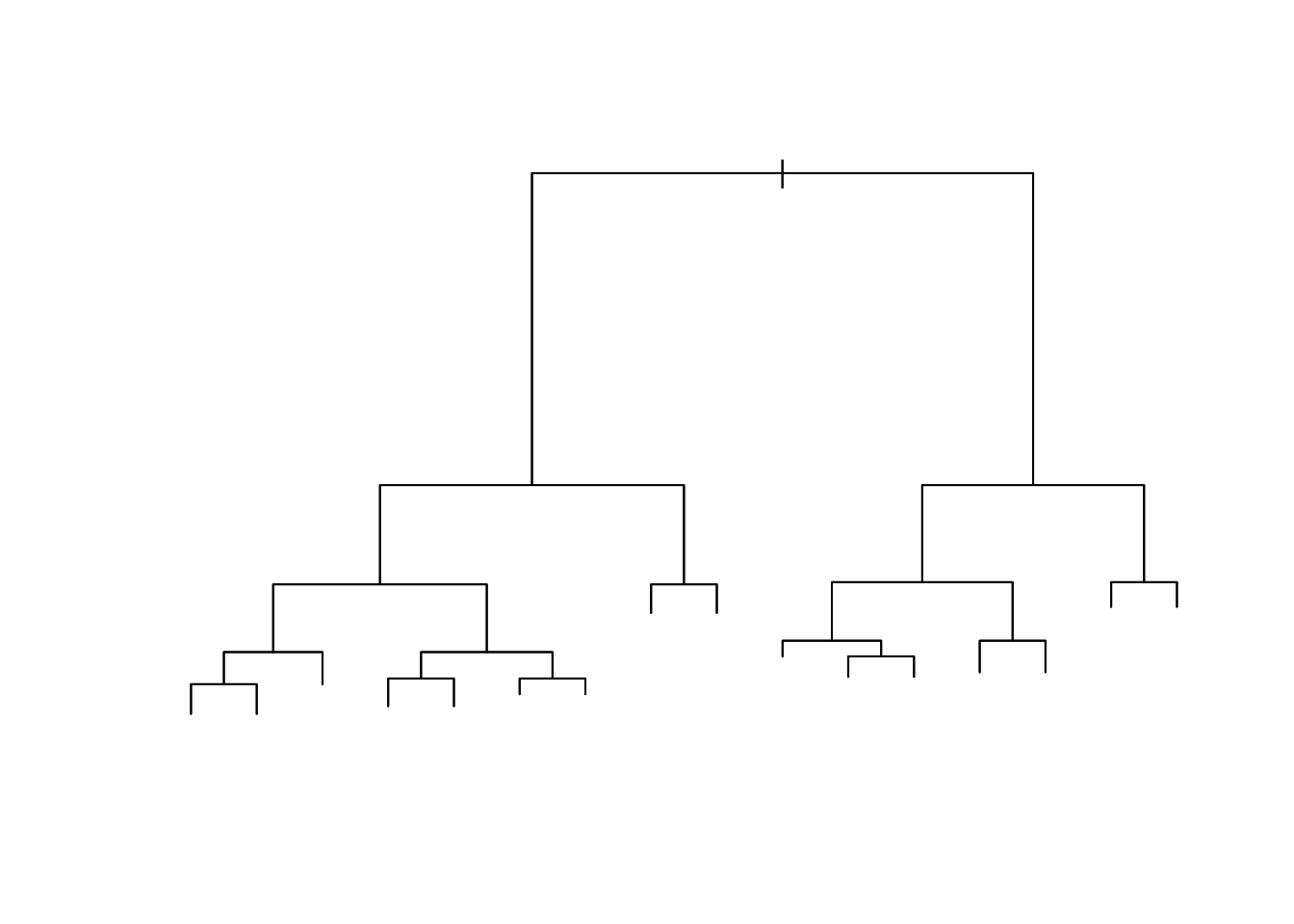
到目前为止,这是一棵非常复杂的树。让我们确定是否可以通过使用分类评分方法的交叉验证来使用修剪后的版本改善拟合度。
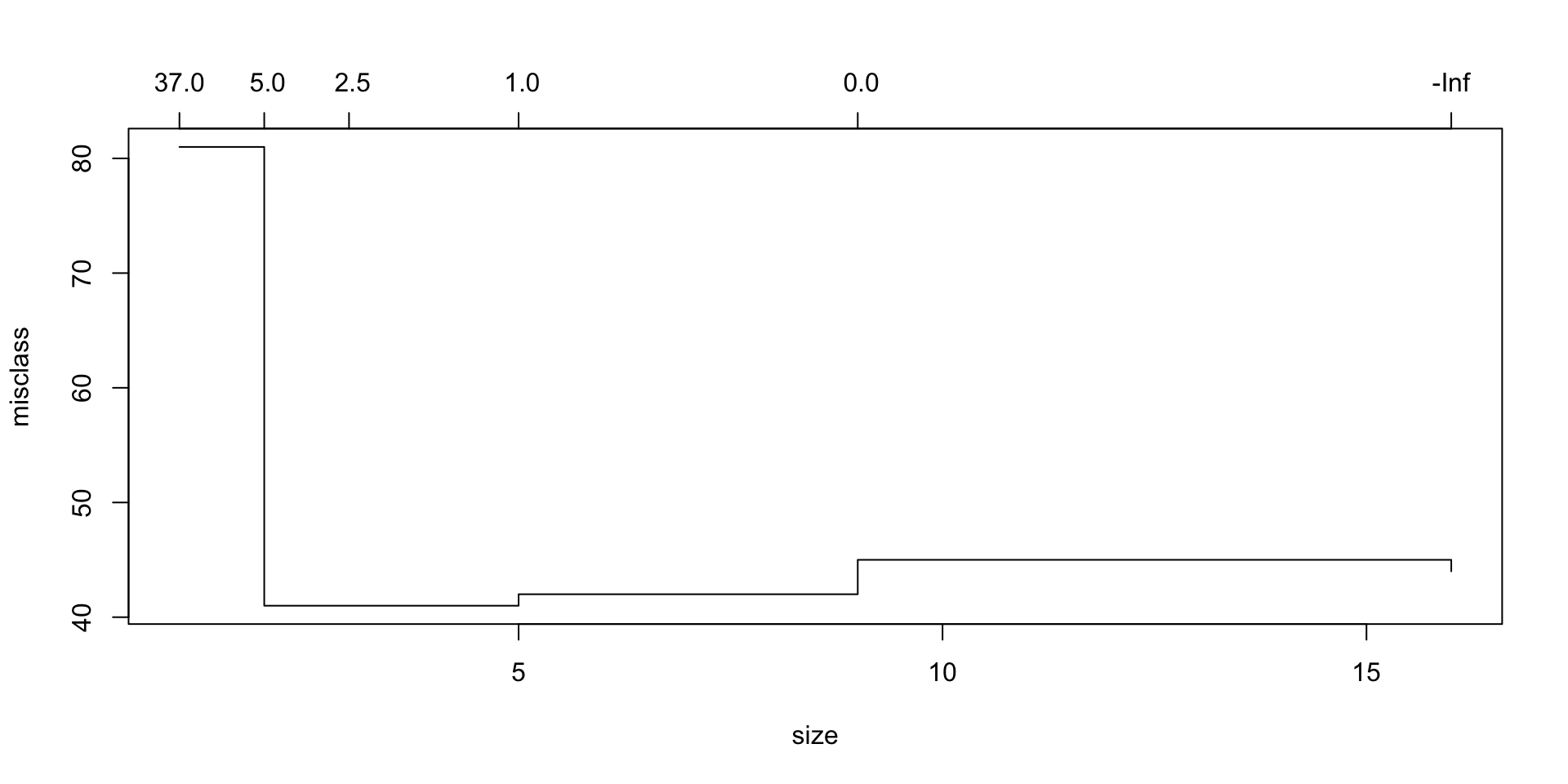
cv.trees## $size
## [1] 16 9 5 3 2 1
##
## $dev
## [1] 44 45 42 41 41 81
##
## $k
## [1] -Inf 0.0 1.0 2.5 5.0 37.0
##
## $method
## [1] "misclass"
##
## attr(,"class")
## [1] "prune" "tree.sequence"看起来4棵分裂树的偏差最小。让我们看看这棵树是什么样子。同样,我们使用 prune.misclass 分类设置。
prune.trees <- prune.misclass(trees, best=4)
plot(prune.trees)
text(prune.trees, pretty=0)
## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 72 24
## Yes 10 45
##
## Accuracy : 0.775
## 95% CI : (0.7, 0.839)
## No Information Rate : 0.543
## P-Value [Acc > NIR] : 2.86e-09
##
## Kappa : 0.539
## Mcnemar's Test P-Value : 0.0258
##
## Sensitivity : 0.878
## Specificity : 0.652
## Pos Pred Value : 0.750
## Neg Pred Value : 0.818
## Prevalence : 0.543
## Detection Rate : 0.477
## Detection Prevalence : 0.636
## Balanced Accuracy : 0.765
##
## 'Positive' Class : No
## 在这里,我们获得了约76%的精度。
那么为什么要进行拆分呢?拆分导致节点纯度提高 ,这可能会在使用测试数据时有更好的预测。
树与线性模型
最好的模型始终取决于当前的问题。如果可以通过线性模型近似该关系,则线性回归将很可能占主导地位。相反,如果我们在特征和y之间具有复杂的,高度非线性的关系,则决策树可能会胜过传统方法。
优点/缺点
优点:
-
树比线性回归更容易解释。
-
更能反映了人类的决策。
-
易于以图形方式显示。
-
可以处理没有伪变量的定性预测变量。
缺点:
- 树木通常不具有与传统方法相同的预测准确性,但是,诸如 Bagging,随机森林和增强等方法 可以提高性能。
其他例子
树结构中实际使用的变量:“价格”、“ CompPrice”、“年龄”、“收入”、“ ShelveLoc”、“广告”,终端节点数:19,残差平均偏差:0.414 = 92/222,错误分类错误率:0.0996 = 24/241
在这里,我们看到训练误差约为9%。我们 plot() 用来显示树结构和 text() 显示节点标签。
plot(sales.tree)
text(sales.tree, pretty=0)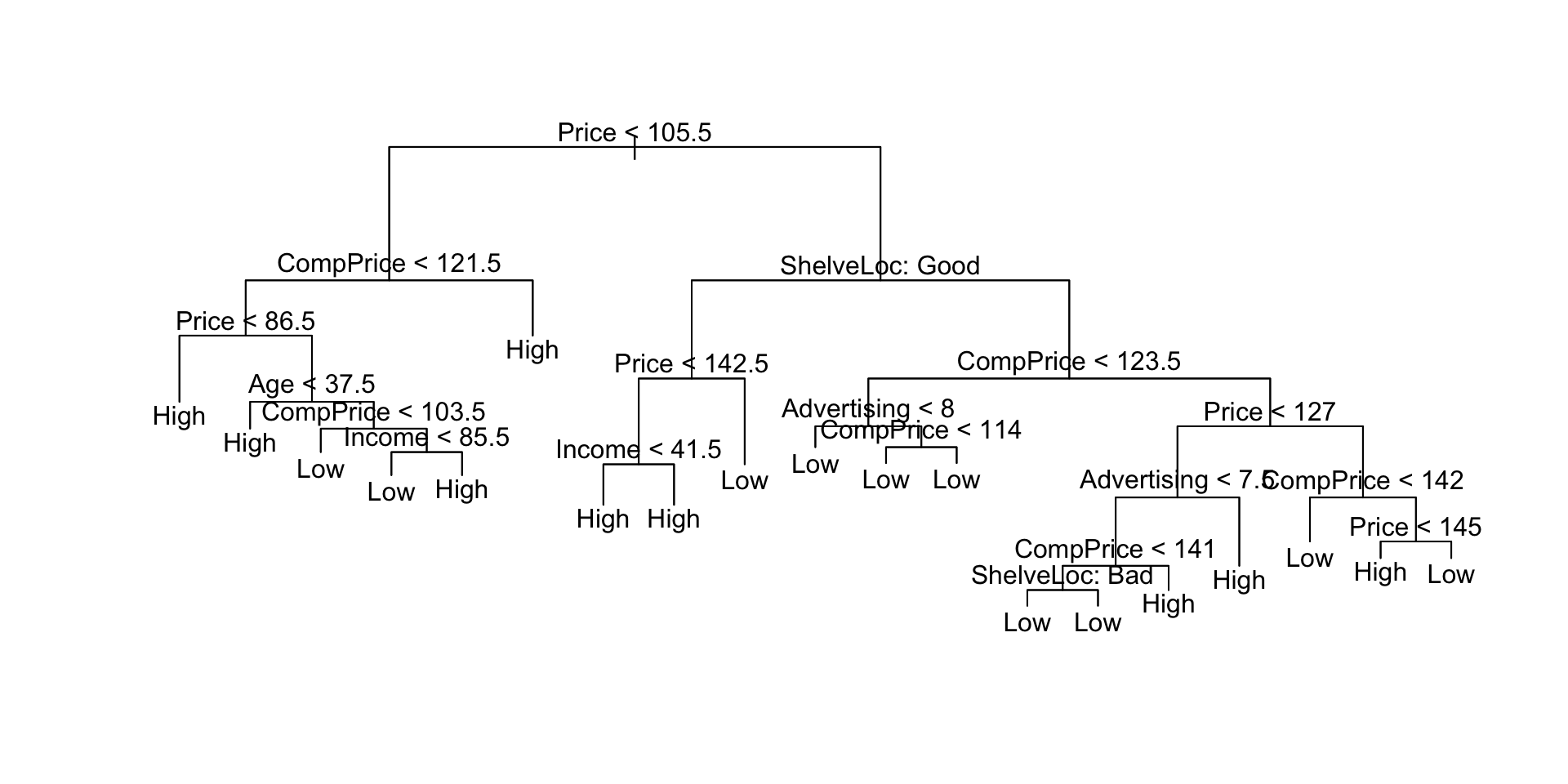
让我们看看完整的树如何处理测试数据。
## Confusion Matrix and Statistics
##
## Reference
## Prediction High Low
## High 56 12
## Low 23 68
##
## Accuracy : 0.78
## 95% CI : (0.707, 0.842)
## No Information Rate : 0.503
## P-Value [Acc > NIR] : 6.28e-13
##
## Kappa : 0.559
## Mcnemar's Test P-Value : 0.091
##
## Sensitivity : 0.709
## Specificity : 0.850
## Pos Pred Value : 0.824
## Neg Pred Value : 0.747
## Prevalence : 0.497
## Detection Rate : 0.352
## Detection Prevalence : 0.428
## Balanced Accuracy : 0.779
##
## 'Positive' Class : High
## 约74%的测试错误率相当不错,但是我们可以通过交叉验证来改善它。
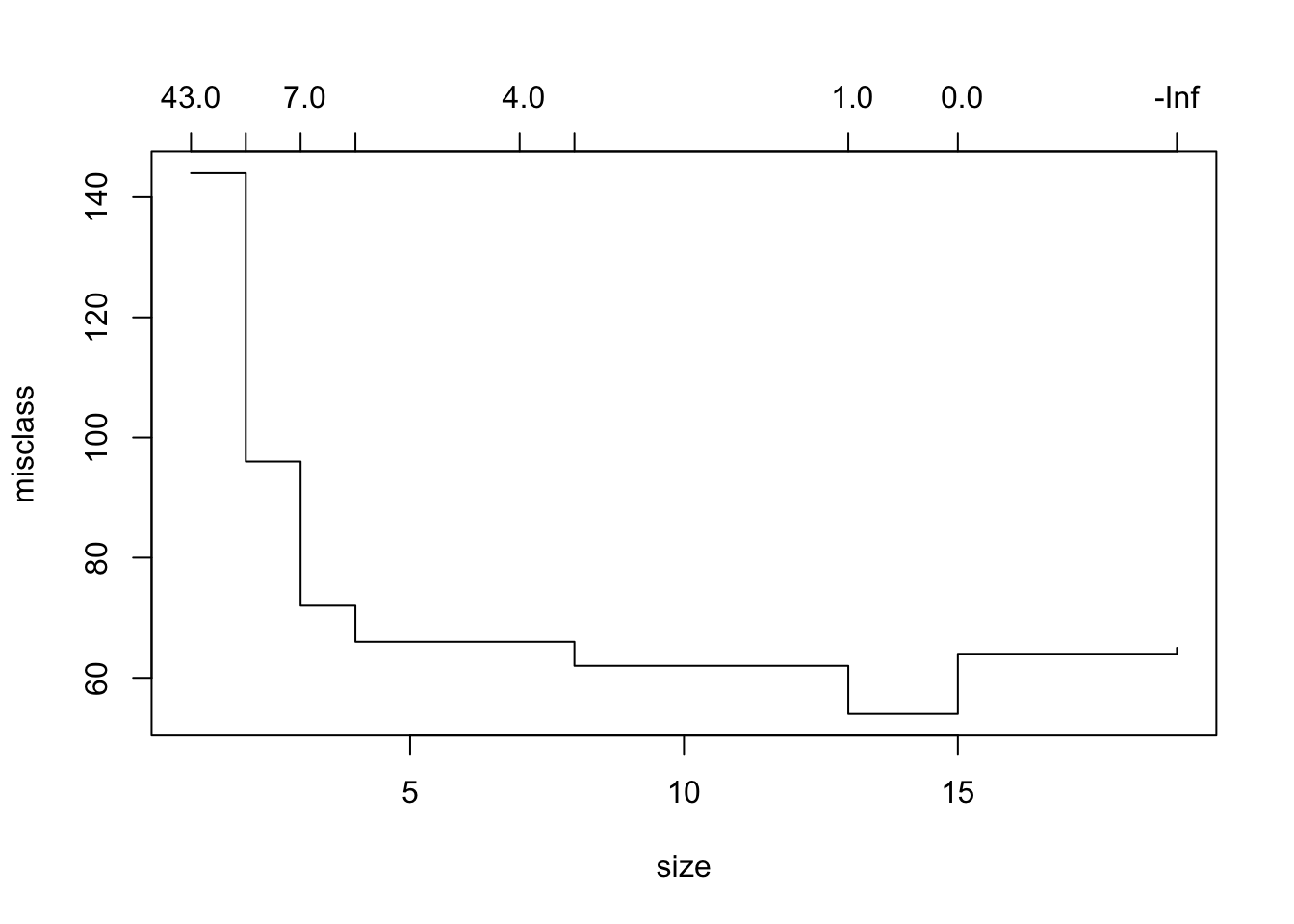
在这里,我们看到最低的错误分类错误是模型4的。现在我们可以将树修剪为4模型。
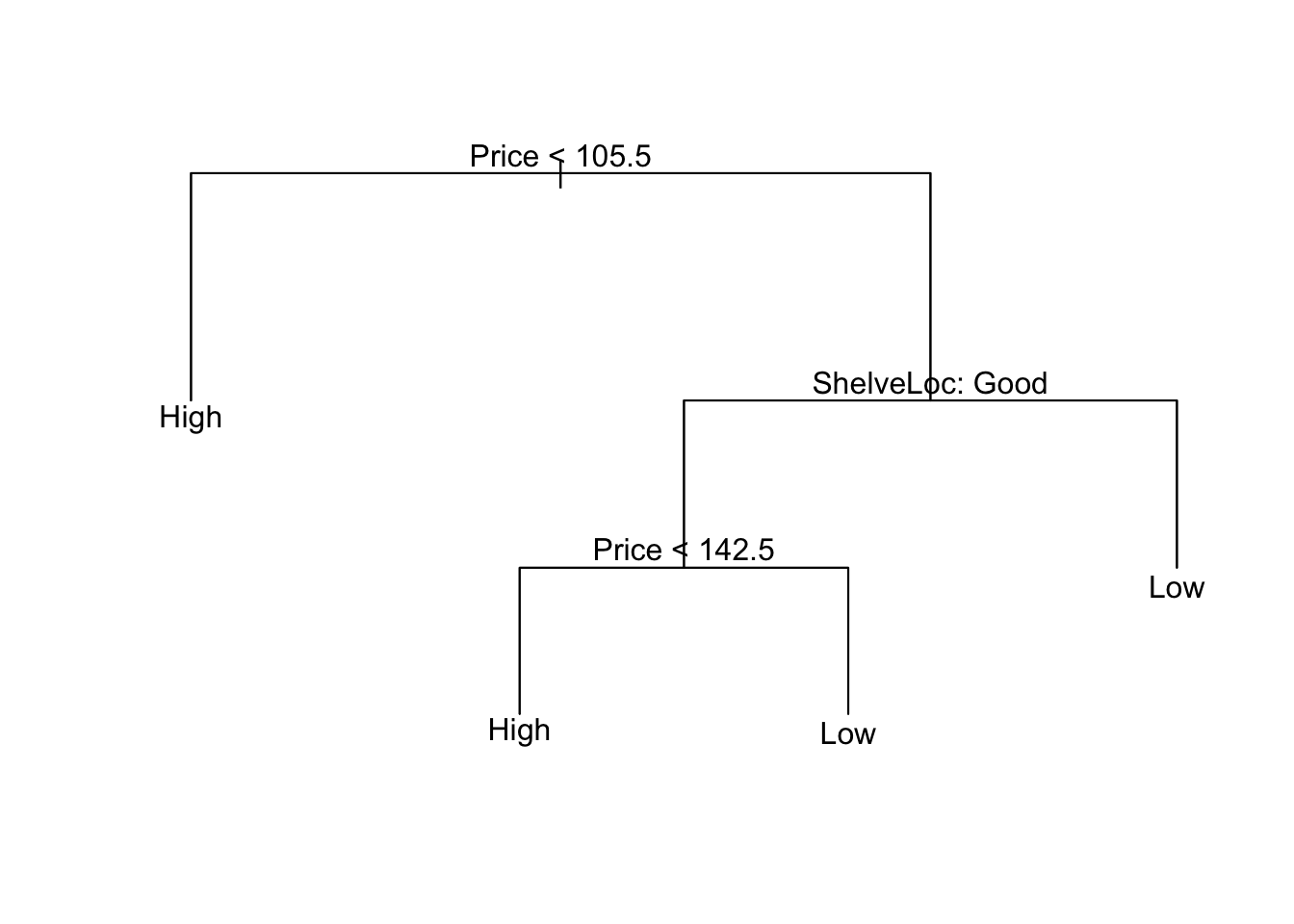
## Confusion Matrix and Statistics
##
## Reference
## Prediction High Low
## High 52 20
## Low 27 60
##
## Accuracy : 0.704
## 95% CI : (0.627, 0.774)
## No Information Rate : 0.503
## P-Value [Acc > NIR] : 2.02e-07
##
## Kappa : 0.408
## Mcnemar's Test P-Value : 0.381
##
## Sensitivity : 0.658
## Specificity : 0.750
## Pos Pred Value : 0.722
## Neg Pred Value : 0.690
## Prevalence : 0.497
## Detection Rate : 0.327
## Detection Prevalence : 0.453
## Balanced Accuracy : 0.704
##
## 'Positive' Class : High
## 这并不能真正改善我们的分类,但是我们大大简化了模型。
## CART
##
## 241 samples
## 10 predictors
## 2 classes: 'High', 'Low'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
##
## Summary of sample sizes: 217, 217, 216, 217, 217, 217, ...
##
## Resampling results across tuning parameters:
##
## cp ROC Sens Spec ROC SD Sens SD Spec SD
## 0.06 0.7 0.7 0.7 0.1 0.2 0.1
## 0.1 0.6 0.7 0.6 0.2 0.2 0.2
## 0.4 0.5 0.3 0.8 0.09 0.3 0.3
##
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was cp = 0.06.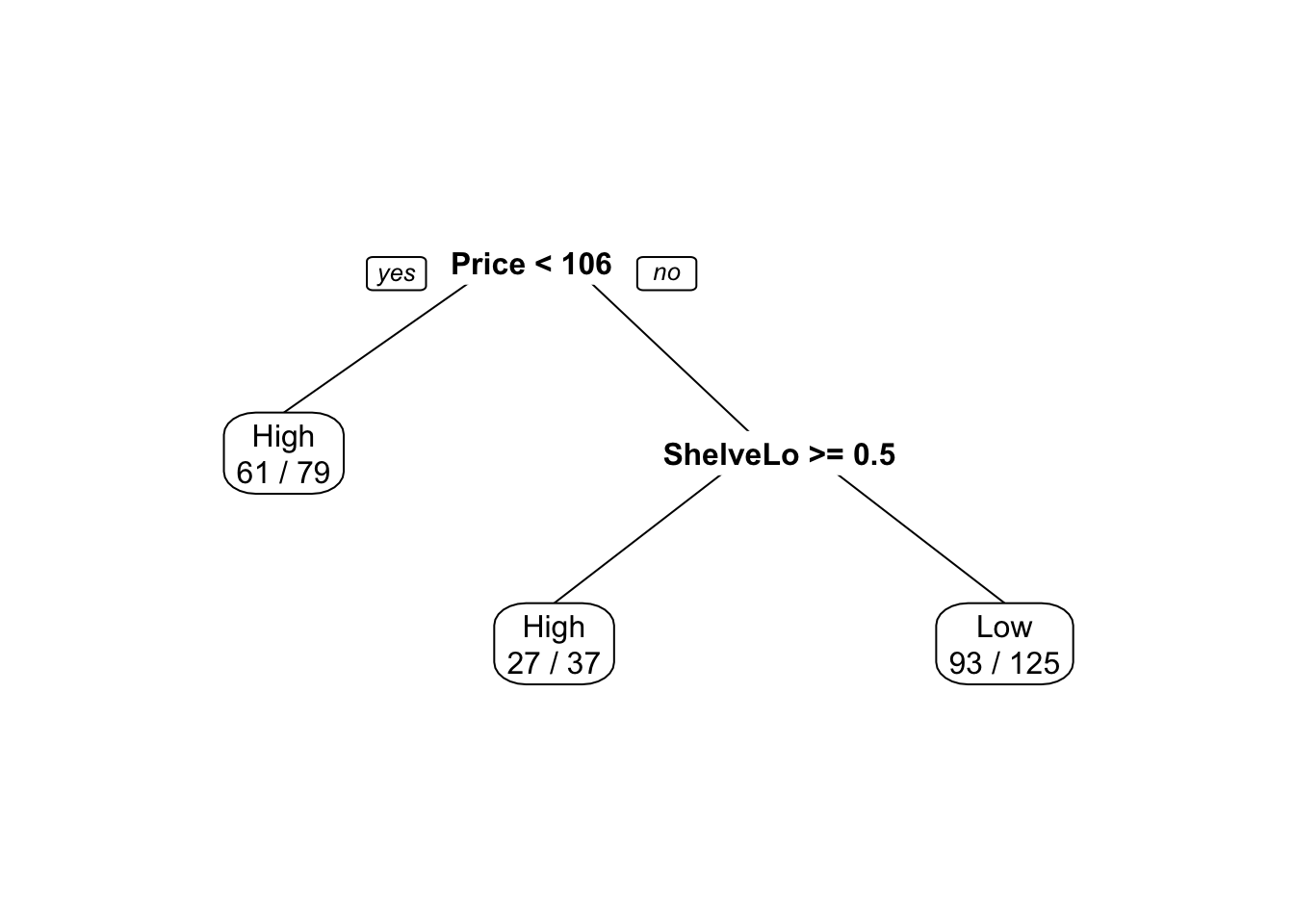
## Confusion Matrix and Statistics
##
## Reference
## Prediction High Low
## High 56 21
## Low 23 59
##
## Accuracy : 0.723
## 95% CI : (0.647, 0.791)
## No Information Rate : 0.503
## P-Value [Acc > NIR] : 1.3e-08
##
## Kappa : 0.446
## Mcnemar's Test P-Value : 0.88
##
## Sensitivity : 0.709
## Specificity : 0.738
## Pos Pred Value : 0.727
## Neg Pred Value : 0.720
## Prevalence : 0.497
## Detection Rate : 0.352
## Detection Prevalence : 0.484
## Balanced Accuracy : 0.723
##
## 'Positive' Class : High
## 选择了更简单的树,预测精度有所降低。