Python解题 - CSDN周赛第14期

本期其实没啥好写的，都是数学题，和算法关系不大，唯手熟尔。而且又出现了同一天的每日一练中包含了赛题，这算不算官方泄题呢？看来下次在竞赛之前先做完每日一练大有益处呢。

第一题：字符串全排列

对K个不同字符的全排列组成的数组，面试官从中随机拿走了一个，剩下的数组作为输入，请帮忙找出这个被拿走的字符串？

比如[“ABC”, “ACB”, “BAC”, “CAB”, “CBA”] 返回 “BCA”

第一行输入整数 $n$ （ $n=K!-1$ ），下面n行，每行输入一组剩下的字符串组合。

示例1
输入
5

ABC

ACB

BAC

CAB

CBA

输出 BCA

分析

一般来讲第一题都是简单题，所以本题虽然使用全排列查找的算法复杂度是 $O(n!)$ ，但因为数据范围不大，依然可以pass。于是只要穷举出输入字母的所有组合，然后找出少了哪一组，就能得到答案。Python可以直接使用内置的排列组合函数permutations，速度会快上不少。

本题n可以等于0，也就是说 $K=1$ ，一个字母的组合，那自然是什么都不缺，所以特判，输出一个空字符串既可。

参考代码1

n = int(input())
vector = [input().strip() for _ in range(n)]
if n == 0:
    print("")
else:
    from itertools import permutations
    res = set()
    for i in permutations(vector[0]):
        res.add("".join(i))
    res.difference_update(set(vector))
    print(res.pop())

优化

然鹅，虽然通过了，我们不应该就此满足。仔细观察一下，就能很快找出本题的“窍门”：

如果 $K$ 个字母的组合没有缺失（总共有 $K!$ 个组合），那么这些组合从左到右的每个位置上，每个字母都出现了 $K-1$ 次。比如ABC三个字母的全排列组合ABC,ACB,BAC,BCA,CAB,CBA，第一位出现的是AABBCC，第二位出现的是BCACAB，第三位出现的是CBCABA，每个位置的每个字母都出现了两次。于是，如果缺少一组的话，那么只要检查所有组合每位上的字母，出现次数最少的就是答案。这里需要加一个特判，当只有两个字母的时候（ $n=1$ ），由于只有两种组合，所以只要翻转过来输出字符串即可。

参考代码2

n = int(input())
vector = [input().strip() for _ in range(n)]
if n == 0:
    print("")
elif n == 1:
    print(vector[0][::-1])
else:
    result = ""
    for i in zip(*vector):
        result += min(i, key=i.count) # 找出出现次数最少的字母
    print(result)

第二题：小Q新式棋盘

已知棋盘大小为n*n。每个位置都有自己的权值q。该棋盘中有多少对行权值和小于列权值和？

示例1 示例2
输入
3

1 2 3

1 2 3

1 2 3

3

4 5 6

2 3 4

3 2 1

输出 3 5

分析

本题只记得第一个示例，但原理很简单，就是分别计算每行、每列的数字之和，然后比较有多少行的数字之和，小于列的数字之和。作为第二题，数据范围自然也不大，所以 $O(n^2)$ 嵌套循环的暴力穷举算法就能pass。

参考代码1

n = int(input())
vector = [list(map(int, input().split())) for _ in range(n)]
row = [sum(i) for i in vector]
col = list(map(sum, zip(*vector)))
result = 0
for i in range(n):
    for j in range(n):
        if row[i] < col[j]:
            result += 1
print(result)

优化

同样，我们不能就此满足，本题其实还有更快的算法。先对行权值和列权值进行排序，然后从小到大依次比较，找到行权值比列权值小的位置，然后累加剩下的列权值个数即可。

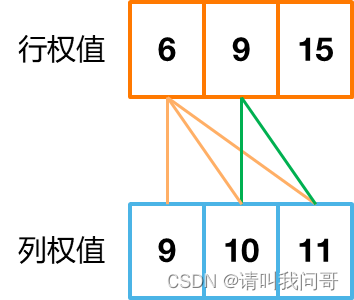
拿示例二举例，我们计算行权值得到列表[15, 9, 6]，排序得到[6, 9, 15]，计算列权值得到列表[9, 10, 11]，比较两个列表的第一个数字，6小于9，所以累加列权值列表9所在位置（包括9）往后的所有数字的个数3（因为9在第一位，所以如果小于第一个9，那么就代表着所有比它后面所有的数都小），然后再比较行权值列表的第二个数字9，因为不小于列权值列表的第一个数字9，所以比较第二个数字10，由于9小于10，所以累加10后面的数字之和2（包括10自己），答案是5。

如果不算计算行、列权值之和的时间复杂度的话，sort排序的时间复杂度是 $O(nlogn)$ ，比较两个等长列表的时间复杂度是 $O(n)$ （其实是2*n，但是惯例舍去系数），所以整体的时间复杂度是 $O(nlogn)$ （只保留最高位）。

参考代码2

n = int(input())
vector = [list(map(int, input().split())) for _ in range(n)]
row = sorted(sum(i) for i in vector)
col = sorted(map(sum, zip(*vector)))
i = j = 0
result = 0
while i < n and j < n:
    while j < n and row[i] >= col[j]:
        j += 1
    result += n-j
    if j == n: break # 所有行权值都比列权值大，就没必要继续比下去了
    i += 1
print(result)

第三题：因数-数字游戏

小Q的柠檬汁做完了，掏出了自己的数字卡牌，想要和别人做数字游戏，可是她又不想要输掉游戏。她制定好规则，每次每个人只能把这个牌换成它的因子的某个牌，但是这个因子不能是1或者整数本身。现在给出整数n，两个人开始做游戏，谁无法再给出因子牌则该人胜利。如果该整数无因子牌直接视为先手胜利。请判断先手在最优策略状态下能否必胜，如果能则输出1，不能则输出2。

示例

示例1 示例2
输入
6

30

输出 2 1

分析

本题出现在了同一天的每日一练中。。。官方泄题嫌疑。

描述看着十分复杂，无牌可出竟然算胜利，以至于计算的过程中老是绕不过来弯。。。其实这道题非常简单。题目已经说了“这个因子不能是1或者整数本身”，这不摆明就是质数（素数）嘛。所以把题意换个说法就是，剩下一个质数（素数）给对手，对方就获胜了。。。（还是很别扭）。结合输出条件（必胜输出1，反之输出2），可以得出以下条件：

如果该数是质数（素数），小Q胜，输出1（起手无牌可出）
如果该数有2个质因数，小Q输，输出2（因为小Q只能打出一个质因数，剩下另一个质数给对方）
如果该数有3个或以上的质因数，小Q胜，输出1（因为小Q可以打出任意两个质因数的乘积替换该数，把上面第二种情况留给对手）

所以，就是简单的判断分支结构。顺便提一句小技巧，计算某数是否是质数（素数）的时候，只要依次试除到该数的平方根即可。

参考代码

n = int(input())
if n < 4: # 如果该数是1、2、3就不用比了，无牌可出
    print(1)
else:
    for i in range(2, int(n**0.5)+1):
        if n%i == 0:
            p = []
            while n > 1:
                while n%i == 0:
                    n //= i
                    p.append(i)
                if len(p) > 2: # 如果有3个以上的质因数，先手胜
                    print(1)
                    break
                i += 1
            else:
                print(2) # 只有2个质因数，比如6，后手胜
            break
    else:
        print(1) # 该数是质数，起手胜

第四题：编码

编码工作常被运用于密文或压缩传输。这里我们用一种最简单的编码方式进行编码：把一些有规律的单词编成数字。字母表中共有26个字母{a，b，…，z}，这些特殊的单词长度不超过6且字母按升序排列。把所有这样的长度相同的单词放在一起，按字典顺序排列（a...z，ab...az，bc...bz....）一个单词的编码就对应着它在整个序列中的位置。你的任务就是对于所给的单词，求出它的编码，如果没有则输出0。

示例：

示例1 示例2
输入
ab

glq

输出 27 1882

分析

本题稍微有点烧脑，但难度并不高，只是比较麻烦。因为“单词长度不超过6”，所以即使穷举，列出所有单词，相信也能过（最后一个单词uvwxyz的编码是313911，所以编码范围就是1到313911）。而本题可以编码的单词字母不允许重复，也必须是按照字母升序排序，所以加个特判，如果输入单词有重复字母，或者不是升序排列，则输出0（就不需要穷举才能证明找不到了）。

但是问哥喜欢找规律，所以这题不满足于穷举（这题明摆着是计算题啊），于是在草稿纸上画出下图（省略右边e到z的列）：

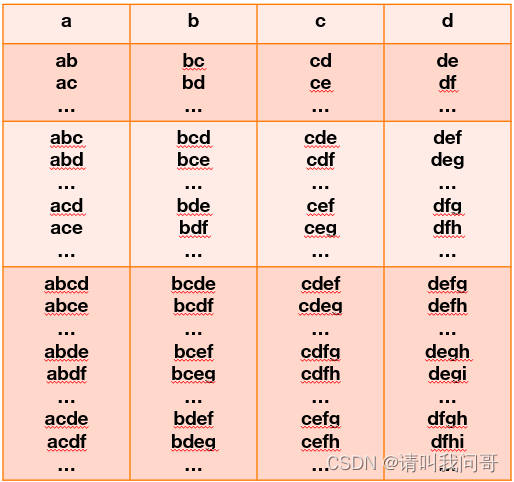
所有单词的排列顺序应该如上图所示，不难发现，每个表格中的单词数量都等于其上一行右边一列算起的个数之和。比如第二行第一列a开头的所有两位单词的个数，就等于第一行第二列字母b及后面字母的个数，也就是25。而第三行第一列a开头的所有三位单词个数，等于第二行bc开始的单词个数，加上cd开始的单词个数，加上de开始的单词个数。。。加上yz开始的单词个数。第四行同理。。。

所以，如果本题算做动态规划的话，把上面二维表的每个格子视作某个字母（列）开始的n位单词（行）的个数，可以得到方程如下：

$dp[i][j] = sum(dp[i-1][j+1:])$

只有第一行，也就是一位字母的那一行，需要全部设置为1，这样就可以通过上面这个公式得到n位单词的一张个数表，而我们要计算单词的排序（编码），只要查表计算就能完成。

计算方法是：从左向右依次取出字母，通过查表找到以该字母开始的n位单词的个数，然后加上所有在它之前的同样长度的单词个数，然后重复此过程，直到最后一个字母。如果设每一位字母在字母表中的位置（顺序）为a[n]，则可得公式如下（公式表达不一定准确，以描述为准 :P）：

$\sum_{i=0}^{n}sum(dp[n-i-1][:a[i]])$

此公式的数学证明比较麻烦，这里就略过了（其实也比较简单，就是统计某个字母开始的第一个单词前面出现了多少单词），但即便不用证明，单纯的观察就可以得到上述规律。

拿示例二的单词glq为例，我们根据前面的制表公式可以得到下面这张表：

然后我们依次查找第一位字母g所在的列，累加它所在行它之前的所有数字（包括它自己），也就是图中从300加到171，然后再取第二位字母l，累加它所在行之前的数字（从25加到14），最后再取第三位字母q，累加它之前的所有数字（17个1），最后得到的结果就是答案：1882。

参考代码

word = input().strip()
n = len(word)
if "".join(sorted(list(word))) != word or len(set(word)) != n:
    print(0)
else:
    dp = [[0]*26 for _ in range(n)]
    for i in range(26):
        dp[0][i] = 1
    for i in range(1, n):
        for j in range(25):
            dp[i][j] = sum(dp[i-1][j+1:])
    result = 0
    for i in range(n):
        a = ord(word[n-i-1])-ord("a")+1
        result += sum(dp[i][:a])
    print(result)