目录

题目：

示例：

分析：

代码：

---

题目：

示例：

分析：

题目给我们一个数组，让我们找出数组的每个非空子数组（不用连续），然后按照公式算出子数组的值，然后返回所有子数组的值的总和。

公式是子数组里最小的数乘上子数组里最大的数的平方。

我们可以从公式中得知，数组的值之和最小值和最大值有关，所以只要我取的子数组的数组范围在两个数之间，那么数组里的其他元素怎么选，最终的值都不会 改变。

那么这类和数值大小有关，又和数组顺序没什么关系的题目，我们都可以把数组给先排序一边。

排序完我们可以发现，可以利用双指针来做，双指针来指向数组的两个元素，表示我以这两个元素为开头和结尾的子数组，从下图（已经以英雄的力量值排完序了）可以看出，以两个元素为开头和结尾的子数组一共是有2*（j-i）个的，而他们的值都等于nums[i]*nums[j]*nums[j]，所以我们不需要得出所有的子数组，因为只要首尾元素相同，那么子数组的数值就是一样的，我们只需要遍历所有子数组可能的首尾，再把对应的数组乘上对应的子数组数量就可以。

还是以下图为例 ，我取1和4为首尾元素 ，那么以1和4位首尾元素的子数组的值为1*4*4=16，然后以1和4位首尾元素的子数组一共有（2^(j-i-1)）个，所以我们只需要两层for循环把所有可能的首尾元素遍历一边，再根据左右指针拿到最小值和最大值算出结果，再乘上对应子数组的数量，再加回答案中。

但是这样会有两个问题，第一个是数值溢出，第二个是超时。

所以我们需要想个别的办法。

我们先把每个元素的以此元素为结尾的子数组的总和求出来，参考下图：

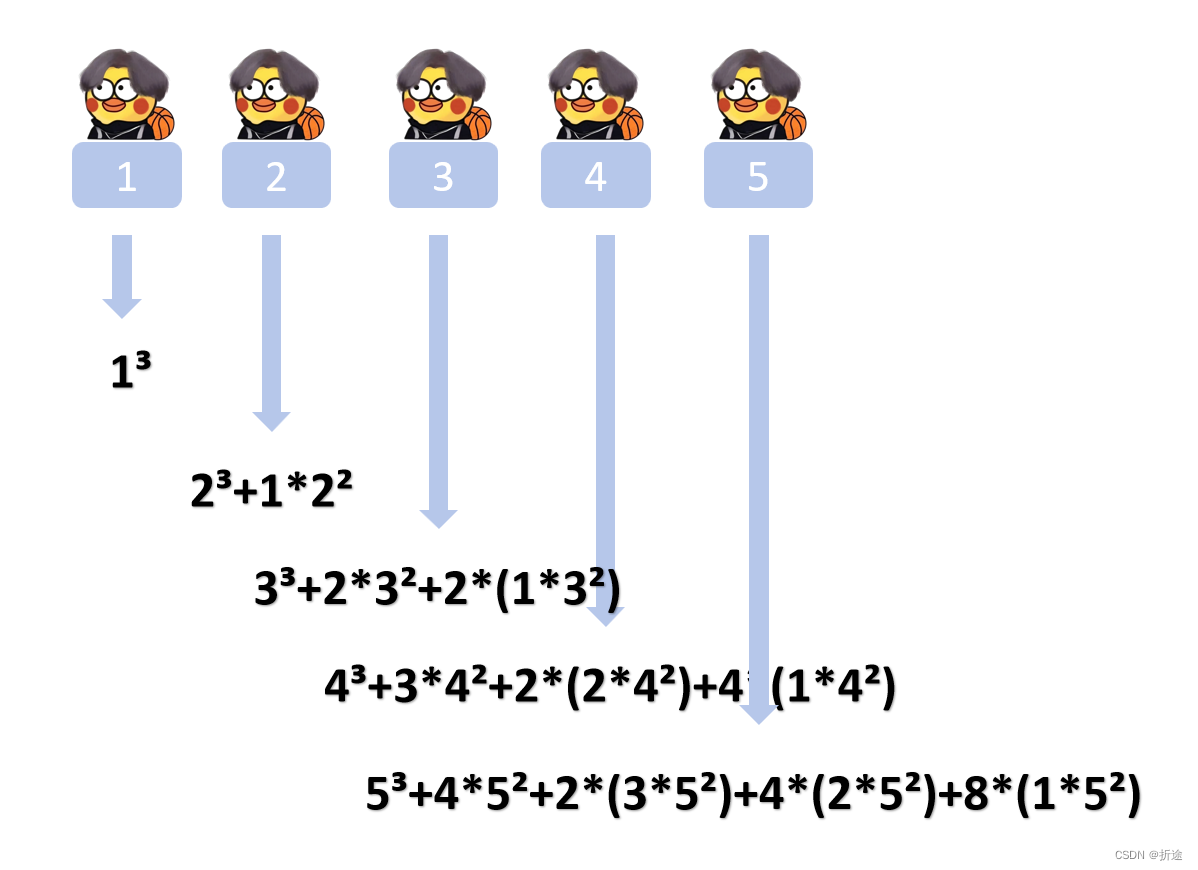
 看起来有些乱，我们化简一下，提出公因子：

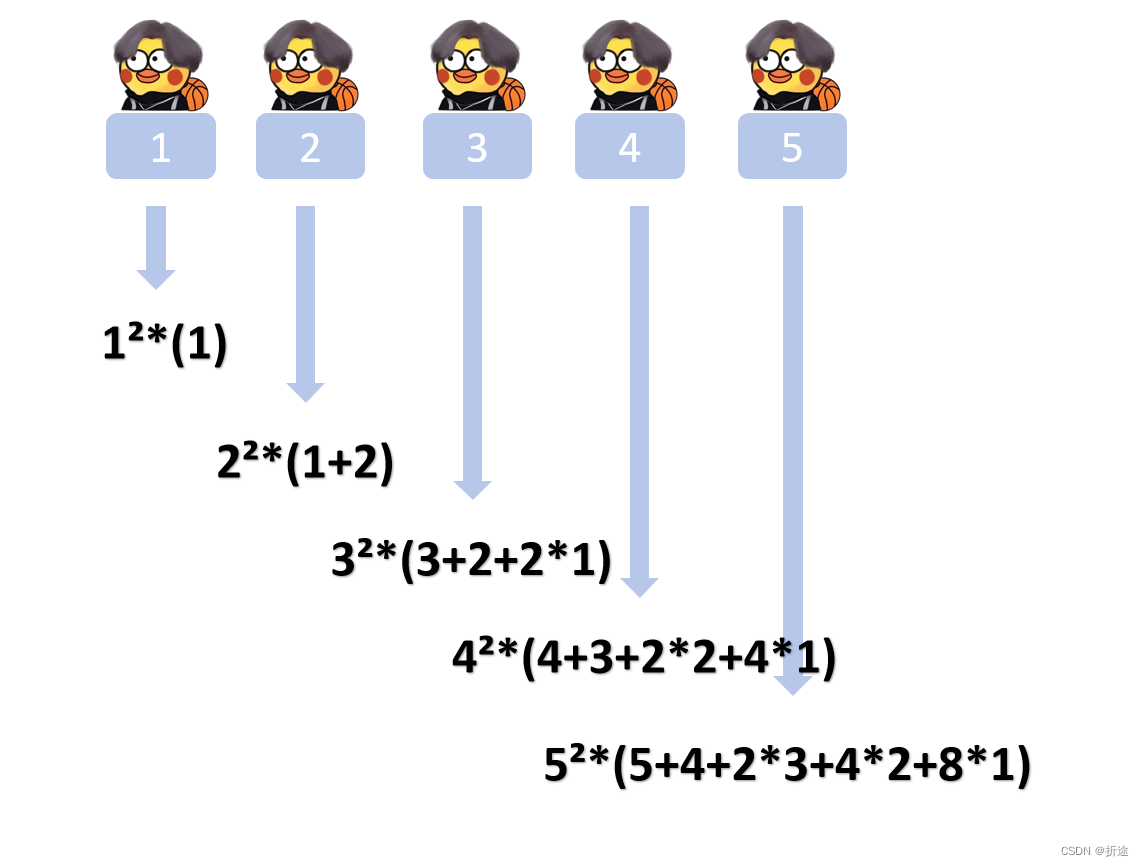
 看起来有些规律了，不过数值的2和代表2个子数组数量的2有些让人分不清，所以我接下来把数值改为字母，因为整个数组是排序后的，因此字母越大就代表数值越大：

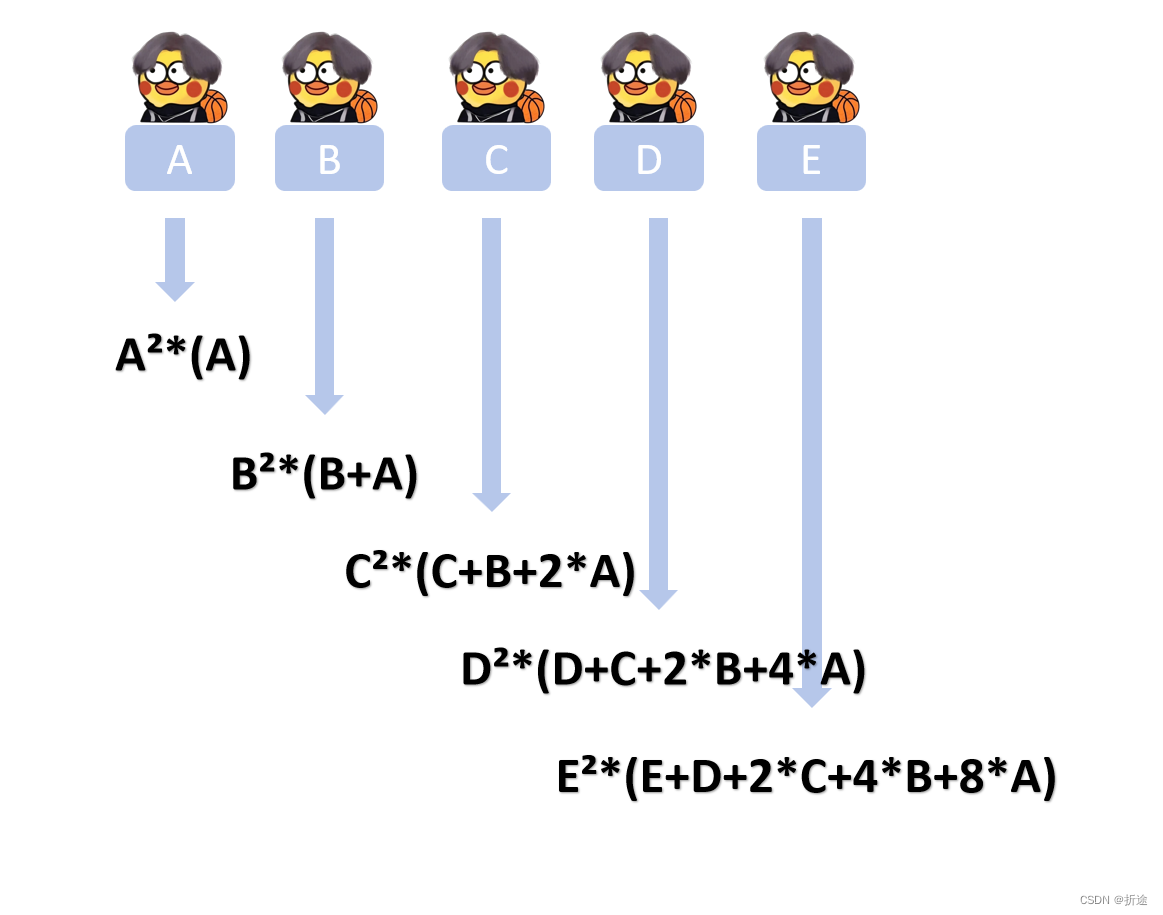
 我们可以发现，每次得出的结果都是当前数的平方乘上当前数再加上上一个数然后在加上一堆看起来有些规律的东西，我们接着分析，看看能不能找出具体的规律。

在第一个数（A）的 前面我们再加一个数（其实数组里没有，只是为了推导出规律才添加上去的），注意标红的表达式，它们是有种继承的关系存在的。

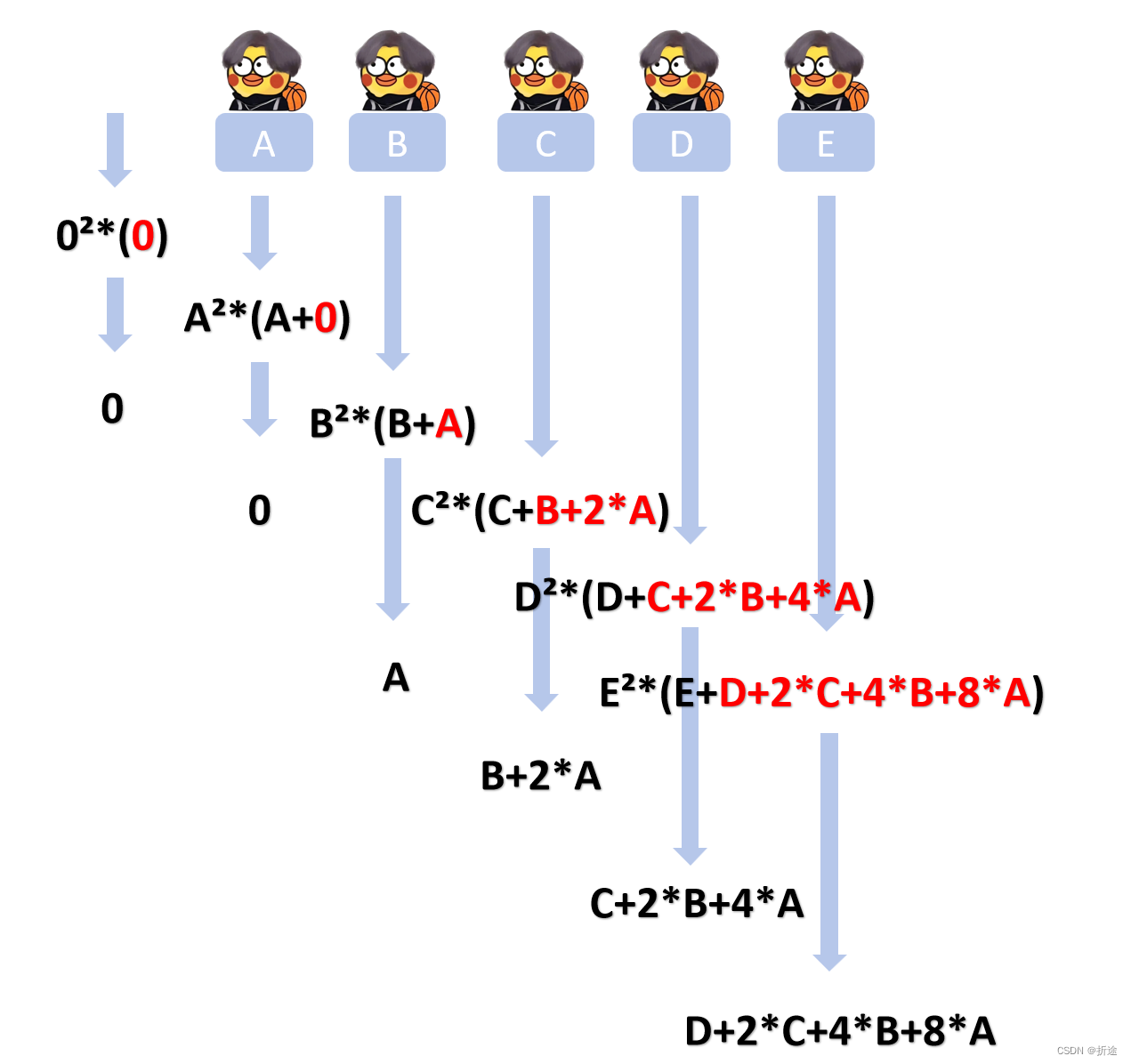
 例如从A开始，标红的是0，因为A前面没有东西了。

B标红的是A。

C标红的是B+2*A。

D标红的是C+2*B+4*A。

发现了吗，除了当前字母的前一个字母，其他都是上一个字母标红的部分乘2。

至此我们已经找出了规律，为了便于归纳，参考下图：

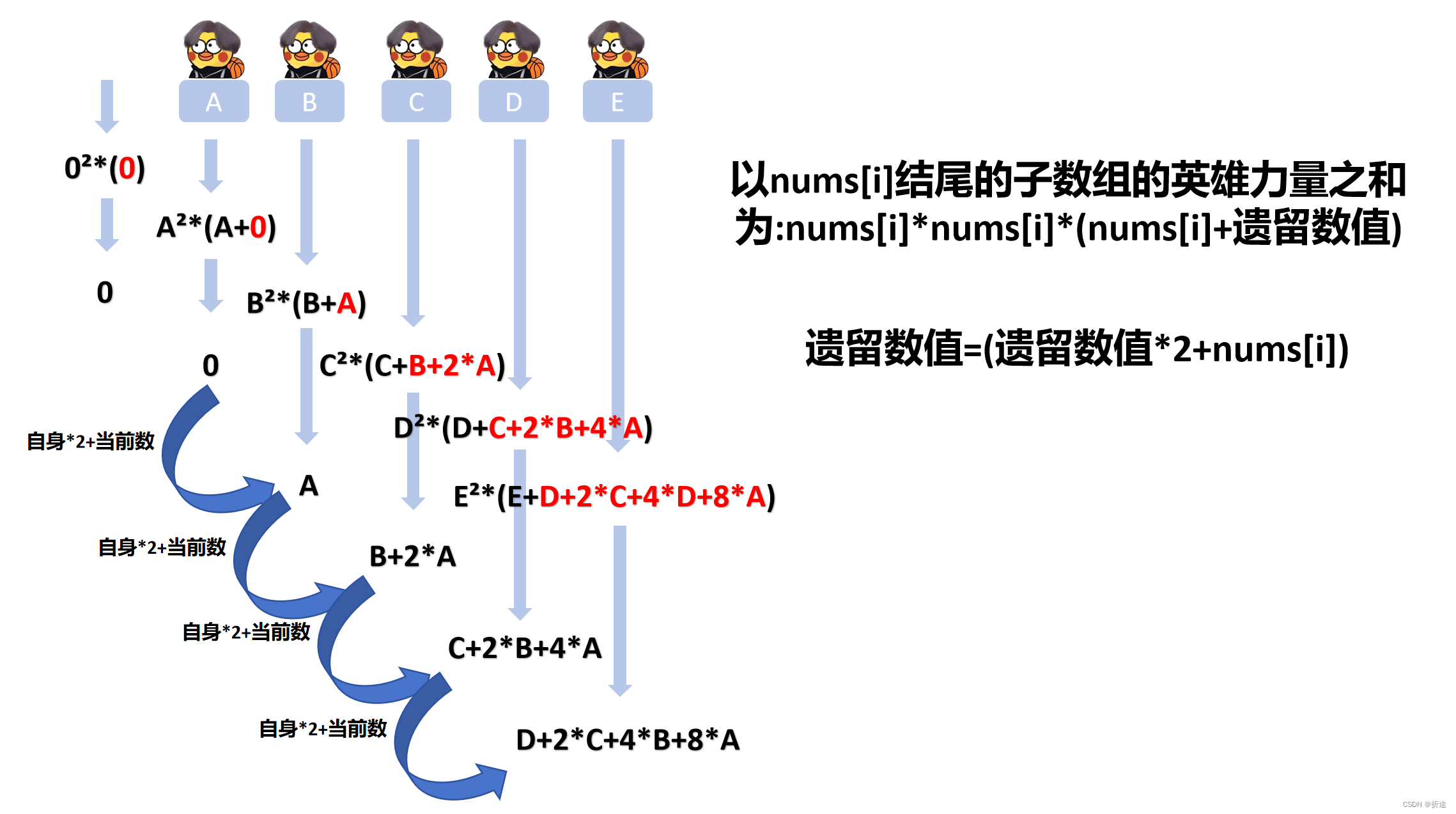
 那么根据上面的两个式子，我们想要解出本题，只需要遍历整个数组一次，时间复杂度比之前的第一种要小了不少。

我们定义一个临时变量来存放标红的部分，每次循环先将当前遍历到的数的平方乘上当前数加上这个临时变量，然后在更新临时变量，也就是临时变量乘2再加上当前遍历到的数。

 遍历完毕，我们也就可以得出题目的答案了。

代码：

class Solution {
public:
    int sumOfPower(vector<int>& nums) {
        sort(nums.begin(),nums.end());    //排序
        unsigned long mod=1000000007;    //记录取模的值
        unsigned long res=0;     //答案
        unsigned long temp=0;    //临时变量
        for(long long num:nums){    
            res+=num*num%mod*(num+temp);    //因为中间可能会数值溢出,因此要取个模
            res%=mod;
            temp=(temp*2+num)%mod;    //更新临时变量
        }
        return res;
    }
};