题意：

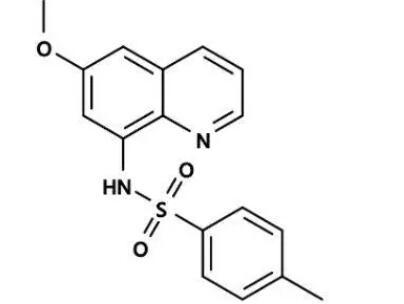
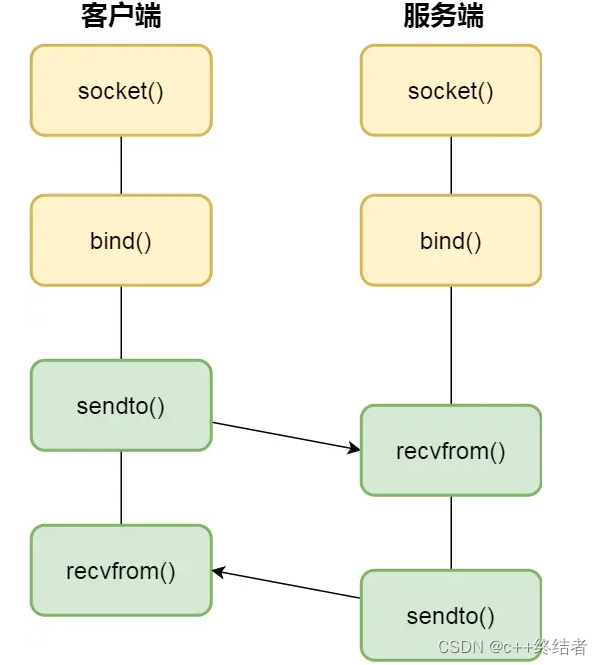
在一个有n个点和m条边的图中找到形状是上图的子图，输出个数

思路：

仔细观察上图，设第二行的那个点为x，最后一行的点为y，那么可以知道，如果x和y都和相同的所有点中取四个点分别和xy相连，并且x和y中任意一个点所连的除了四个共同点之外（如果和另一个点相连也得减去另一个点的个数）的点里随意选两个点，那么就可以构成这个子图

设都与x和y相连的点有cnt个，与x相连的点有num1个，与y相连的点有num2个，那么可以得出子图的个数是：

C（cnt，4）*（ C（num1 - 4 ，2 ）+C（num2 - 4， 2））

对于找x和y的相同点，我们可以用bitset来找，f[i][j]=1表示i和j之间有一条边，算都与x和y相连的点只用算f[i]&f[j]即可

#include<bits/stdc++.h>
#include<bitset>
#define int long long
using namespace std;
const int N=1005,mod=1000000007;
bitset<N> f[N];
int ff[N],fi[N];
int n,m;
int d[N];
int ksm(int a,int b){
	int res=1%mod;
	while(b){
		if(b&1)res=res*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return res;
}
void init(){
	ff[0]=fi[0]=1;
	for(int i=1;i<N;i++){
		ff[i]=(ff[i-1]*i)%mod;
		fi[i]=(fi[i-1]*ksm(i,mod-2))%mod;
	}
}
void sove(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		d[i]=0;
	}
	for(int i=1;i<=n;i++){
		f[i].reset();
	}
	while(m--){
		int a,b;
		cin>>a>>b;
		d[a]++;
		d[b]++;
		f[a].set(b);
		f[b].set(a);
	}
	bitset<N> op;
	int ans=0;
	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			op=f[i]&f[j];
			int num1=d[i]-4;
			int num2=d[j]-4;
			if(f[i][j]==1){
				num1--;
				num2--;
			}
			int x=op.count();
			if(x>=4){
				if(num1>=2){
					int op1=(ff[x]*fi[4]%mod*fi[x-4])%mod;
					int op2=(ff[num1]*fi[2]%mod*fi[num1-2])%mod;
					ans=(ans+op1*op2%mod)%mod;
				}
				if(num2>=2){
					int op1=(ff[x]*fi[4]%mod*fi[x-4])%mod;
					int op2=(ff[num2]*fi[2]%mod*fi[num2-2])%mod;
					ans=(ans+op1*op2%mod)%mod;
				}
			}
		}
	}
	cout<<ans<<endl;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(),cout.tie();
	init();
	int t;
	cin>>t;
	while(t--){
		sove();
	}
	return 0;
}