1.线性枚举
1.线性枚举定义
线性枚举指的就是遍历某个一维数组(顺序表)的所有元素,找到满足条件的那个元素并且返回,返回值可以是下标,也可以是元素本身。
由于是遍历的,穷举了所有的情况,所以一定是可以找到解的,一些资料上也称为暴力算法
2.举例说明
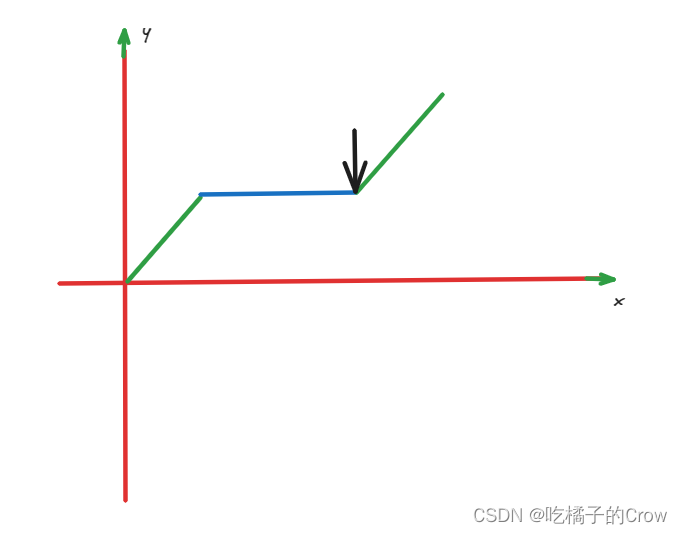
给定一个单调递增的有序数组num和一个x,要求找到大于x的最小数的下标
我们可以将数组以x作为一个分界线,一部分是小于x,一部分是大于或等于x的

遍历去找指针由红色变到绿色的分界线,进行取值
2.二分枚举(具有单调性)
二分枚举,也叫二分查找,指的是给定一个区间,每次选择区间的中点,并且判断区间中点是否满足某个条件,从而选择左区间继续求解还是右区间继续求解,直到区间长度不能再切分为止,由于每次都是把区间折半,又叫折半查找,时间复杂度O(logn),和线性枚举的求解结果一致,但是高效很多,返回的可以是下标也可以是值
栗子:
假如你现在准备去做个实验,实验的内容是求出楼层最高多少层往下扔鸡蛋,鸡蛋不会碎,比如我们采用线性枚举,得从第一层扔,如果没碎,就在第二层层,假设鸡蛋能够承受的高度是50层,则我们得扔50次鸡蛋,钱包可撑不住O(n),但是我们使用二分枚举,第一次取半,在25层进行扔,如果碎了,我们就可以接着在0~25之间再进行取半操作,但是我们这个鸡蛋可是蛋中贵族,我们就需要在25~50层继续进行取半操作,这样时间复杂度就是O(logn)的,楼层越高,二分枚举的效率就越发的明显(万一你刚好一试,鸡蛋刚好没碎!!!)

1.普通的二分查找

public int binarySearch(int [] nums,int target){
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;
}else if(nums[mid]>target){
right=mid-1;
}else{
left=mid+1;
}
}
return -1;
}2.左侧的二分查找

public int binarySearch(int [] nums,int target){
int left=0;
int right=nums.length;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
right=mid;
}else if(nums[mid]>target){
//不断的缩右边界
right=mid;
}else{
left=mid+1;
}
}
return left;
}3.右侧的二分查找
public int binarySearch(int [] nums,int target){
int left=0;
int right=nums.length;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]==target){
right=left+1;
}else if(nums[mid]>target){
right=mid;
}else{
//不断的去缩左边界
left=mid+1;
}
}
return left-1;
}以上的模板在做题的过程中经常可以用得到,希望大家可以仔细的弄明白其中的原理,以后遇到就不用怕了
leetcood题单:
x的平方根
//利用二分查找进行求解
public int mySqrt(int x) {
if(x==0||x==1){
return x;
}
int r=find(x,0,x);
return r-1;
}
public boolean isGree(int val,int x){
return (long)val*val>x;
}
public int find(int x,int left,int right){
if(left>right){
return 0;
}
//找到最右侧的第一个红色
while(left<right){
int mid=left+(right-left)/2;
if(isGree(mid,x)){
right=mid;
}else{
left=mid+1;
}
}
return left;
}第一个错误的版本
public int firstBadVersion(int n) {
int left = 1, right = n;
while (left < right) { // 循环直至区间左右端点相同
int mid = left + (right - left) / 2; // 防止计算时溢出
if (isBadVersion(mid)) {
right = mid; // 答案在区间 [left, mid] 中
} else {
left = mid + 1; // 答案在区间 [mid+1, right] 中
}
}
// 此时有 left == right,区间缩为一个点,即为答案
return left;
}早餐组合
public int breakfastNumber(int[] staple, int[] drinks, int x) {
Arrays.sort(drinks);
Arrays.sort(staple);
int left=0;
int right=drinks.length-1;
int count=0;
int MOD=1000000007;
//左右
while(left<staple.length&&right>=0){
if(staple[left]+drinks[right]>x){
right--;
}else{
count=(count+right+1)%MOD;
left++;
}
}
return count;
}