【本节目标】
1. 掌握方法的定义以及使用
2. 掌握方法传参
3. 掌握方法重载
4. 掌握递归

目录
1.方法概念及使用
1.1什么是方法(method)
1.2 方法定义
1.3 方法调用的执行过程
1.4 实参和形参的关系
2. 方法重载
2.1 为什么需要方法重载
2.2 方法重载概念
3. 递归
3.1 生活中的故事
3.2 递归的概念
3.3 递归执行过程分析
3.4 递归练习
1.方法概念及使用
1.1什么是方法(method)
方法就是一个代码片段. 类似于 C 语言中的 "函数"。方法存在的意义(不要背, 重在体会):
1. 是能够模块化的组织代码(当代码规模比较复杂的时候).
2. 做到代码被重复使用, 一份代码可以在多个位置使用.
3. 让代码更好理解更简单.
4. 直接调用现有方法开发, 不必重复造轮子.
1.2 方法定义
方法语法格式

比如:实现一个两个整数相加的方法
public static int add(int x,int y){
return x+y;
}
写一个方法,检测一个年份是否为闰年
public static boolean isLeapYear(int year) {
if ((year % 3 == 0 && year % 100 != 0) || (year % 400 == 0)) {
return true;
}
return false;
}【注意事项】
1. 修饰符:现阶段直接使用public static 固定搭配
2. 返回值类型:如果方法有返回值,返回值类型必须要与返回的实体类型一致,如果没有返回值,必须写成 void
3. 方法名字:采用小驼峰命名
4. 参数列表:如果方法没有参数,()中什么都不写,如果有参数,需指定参数类型,多个参数之间使用逗号隔开
5. 方法体:方法内部要执行的语句
6. 在java当中,方法必须写在类当中
7. 在java当中,方法不能嵌套定义
8. 在java当中,没有方法声明一说
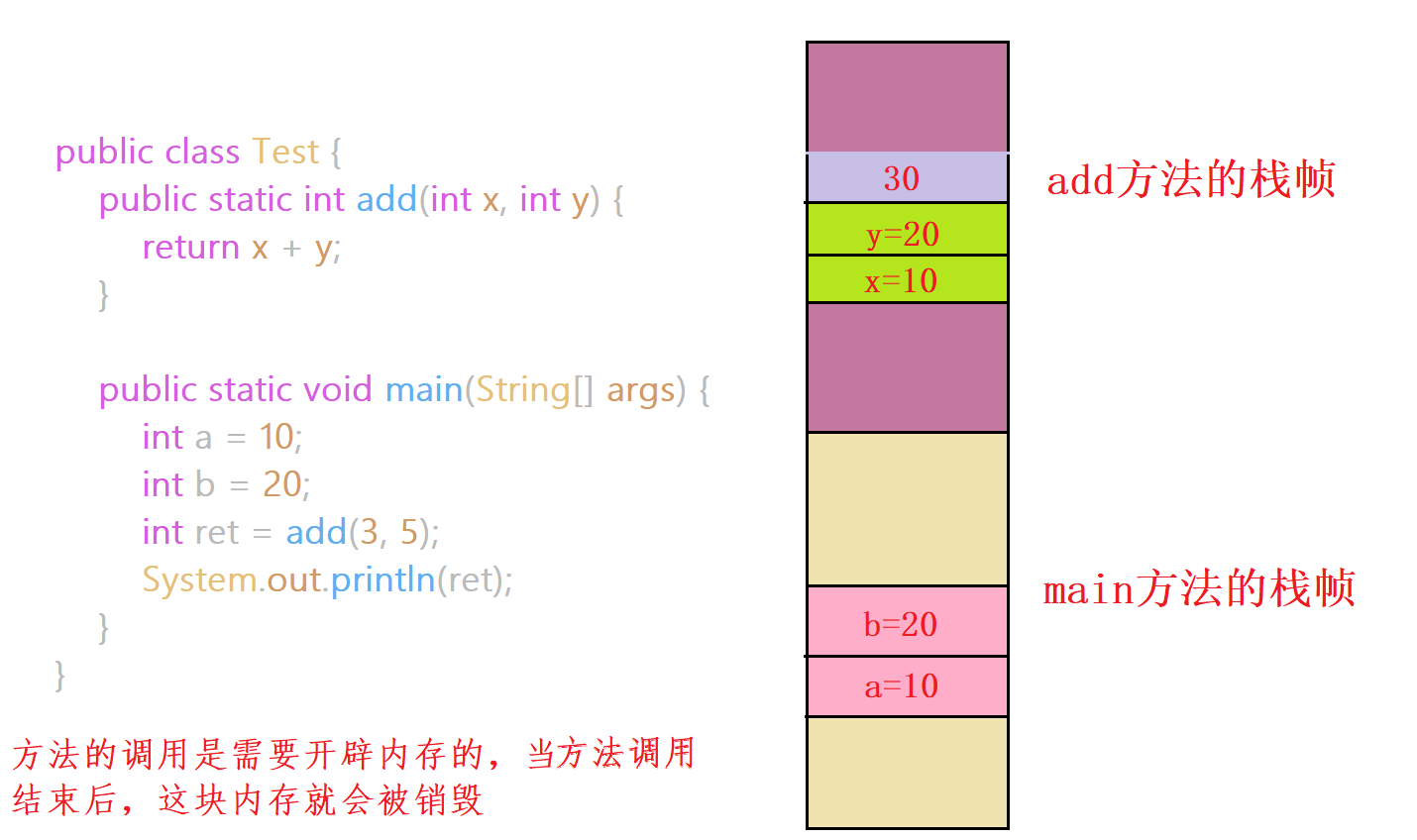
1.3 方法调用的执行过程
【方法调用过程】
调用方法--->传递参数--->找到方法地址--->执行被调方法的方法体--->被调方法结束返回--->回到主调方法继续往下执行
【注意事项】
- 定义方法的时候, 不会执行方法的代码. 只有调用的时候才会执行.
- 一个方法可以被多次调用
代码示例: 计算 1! + 2! + 3! + 4! + 5!
public class Test {
//求n的阶乘
public static int fac(int n) {
int ret = 1;
for (int i = 1; i <= n; i++) {
ret *= i;
}
return ret;
}
//求阶乘和
public static int facSum(int k){
int sum = 0;
for (int i = 1; i <= k; i++) {
sum+=fac(i);
}
return sum;
}
public static void main(String[] args) {
int ret = facSum(5);
System.out.println(ret);
}
}1.4 实参和形参的关系
方法的形参相当于数学函数中的自变量,比如:1 + 2 + 3 + … + n的公式为sum(n) =![]()
Java中方法的形参就相当于sum函数中的自变量n,用来接收sum函数在调用时传递的值的。形参的名字可以随意取,对方法都没有任何影响,形参只是方法在定义时需要借助的一个变量,用来保存方法在调用时传递过来的值。

再比如:

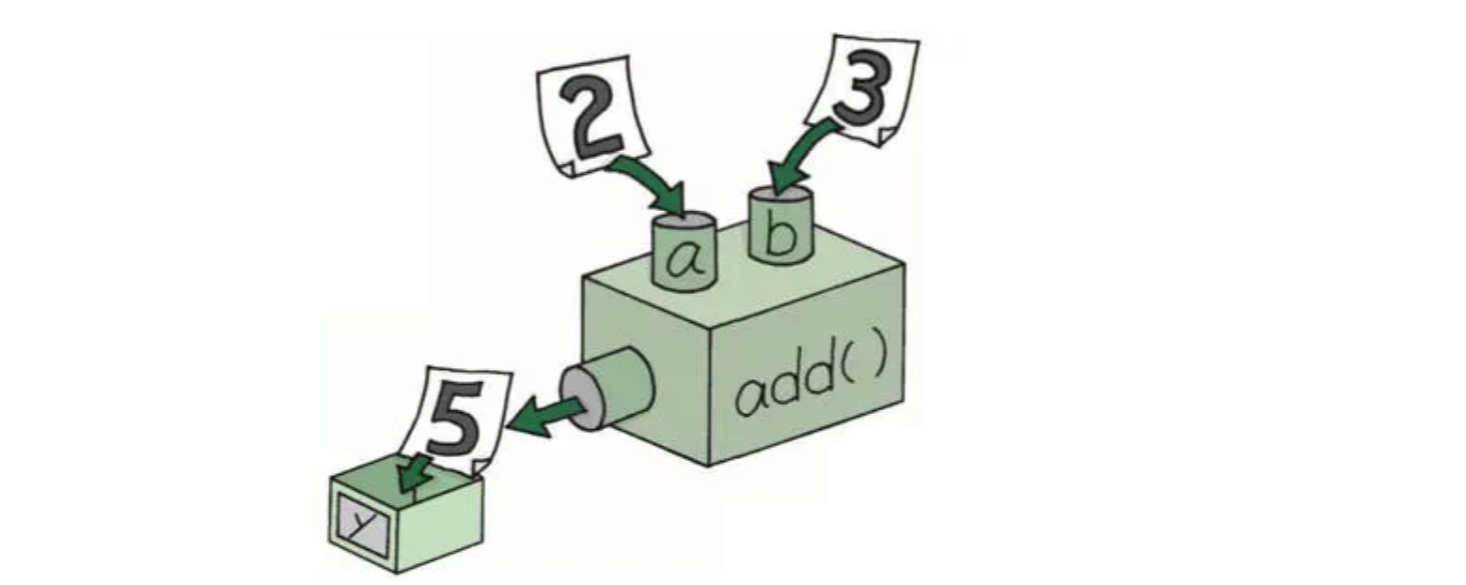
注意:在Java中,实参的值永远都是拷贝到形参中,形参和实参本质是两个实体
代码示例: 交换两个整型变量
public class TestMethod {
public static void main(String[] args) {
int a = 10;
int b = 20;
swap(a, b);
System.out.println("main: a = " + a + " b = " + b);
}
public static void swap(int x, int y) {
int tmp = x;
x = y;
y = tmp;
System.out.println("swap: x = " + x + " y = " + y);
}
}
// 运行结果
swap: x = 20 y = 10
main: a = 10 b = 20可以看到,在swap函数交换之后,形参x和y的值发生了改变,但是main方法中a和b还是交换之前的值,即没有交 换成功。
【原因分析】
实参a和b是main方法中的两个变量,其空间在main方法的栈(一块特殊的内存空间)中,而形参x和y是swap方法中 的两个变量,x和y的空间在swap方法运行时的栈中,因此:实参a和b 与 形参x和y是两个没有任何关联性的变量, 在swap方法调用时,只是将实参a和b中的值拷贝了一份传递给了形参x和y,因此对形参x和y操作不会对实参a和b 产生任何影响。
注意:对于基础类型来说, 形参相当于实参的拷贝. 即 传值调用
【解决办法】: 传引用类型参数 (例如数组来解决这个问题)
public class TestMethod {
public static void main(String[] args) {
int[] arr = {10, 20};
swap(arr);
System.out.println("arr[0] = " + arr[0] + " arr[1] = " + arr[1]);
}
public static void swap(int[] arr) {
int tmp = arr[0];
arr[0] = arr[1];
arr[1] = tmp;
}
}
// 运行结果
arr[0] = 20 arr[1] = 102. 方法重载
2.1 为什么需要方法重载
仍然以之前的加法函数为例子:
public class Test{
public static int addInt(int a, int b){
return a+b;
}
public static void main(String[] args){
int x = 10;
int y = 20;
int ret = addInt(x,y);
System.out.println(ret);
}
}这串代码是可以正常运行的,但是有一个局限,那就是当我们是实参不是int类型的数据时,程序就会出错:
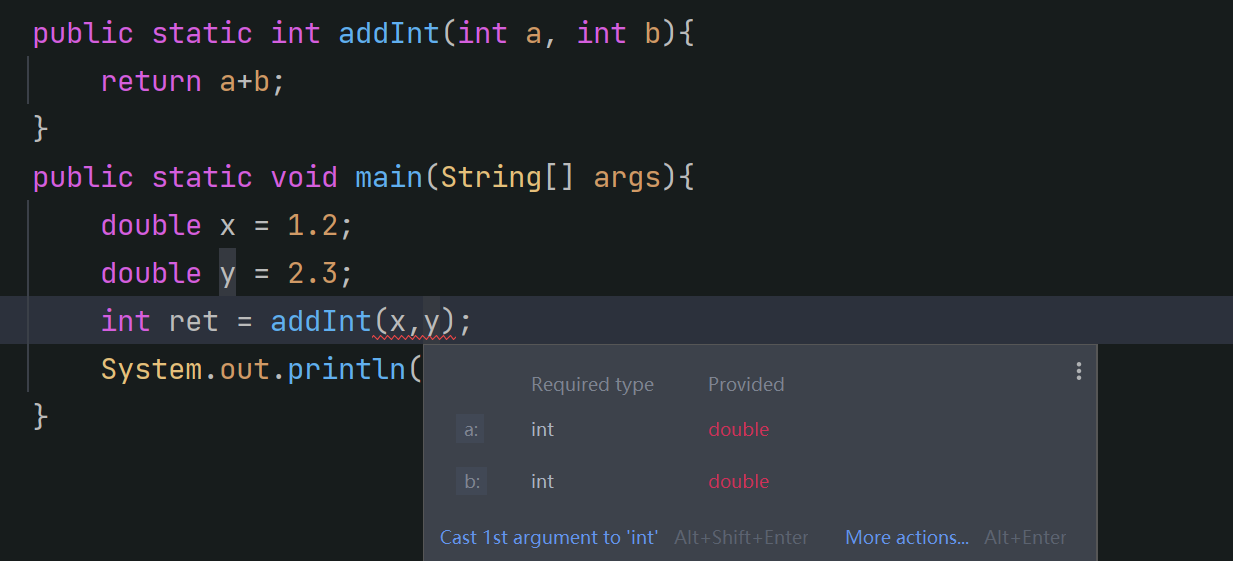
由于参数类型不匹配, 所以不能直接使用现有的 add 方法.
2.2 方法重载概念
在Java中,方法重载(Method Overloading)是指在同一个类中可以存在多个同名的方法,但它们的参数列表不同。通过方法重载,可以根据传入的不同参数来调用不同的方法实现,提供了更灵活和方便的方式来处理不同的情况。
方法重载的规则如下:
- 方法名称必须相同。
- 方法参数列表必须不同,可以通过参数的个数、类型或顺序进行区分。
方法重载与返回值类型是否相同无关
两个方法如果仅仅只是因为返回值类型不同,是不能构成重载的
下面是一个示例来说明方法重载的概念:
public class MyClass {
public static void main(String[] args) {
int sum1 = addNumbers(2, 3);
double sum2 = addNumbers(2.5, 3.8);
int sum3 = addNumbers(1, 2, 3);
System.out.println("Sum1: " + sum1);
System.out.println("Sum2: " + sum2);
System.out.println("Sum3: " + sum3);
}
public static int addNumbers(int a, int b) {
return a + b;
}
public static double addNumbers(double a, double b) {
return a + b;
}
public static int addNumbers(int a, int b, int c) {
return a + b + c;
}
}3. 递归
3.1 生活中的故事
从前有坐山,山上有座庙,庙里有个老和尚给小和尚将故事,讲的就是:
"从前有座山,山上有座庙,庙里有个老和尚给小和尚讲故事,讲的就是:
"从前有座山,山上有座庙..."
"从前有座山……" "

上面的两个故事有个共同的特征:自身中又包含了自己,该种思想在数学和编程中非常有用,因为有些时候,我们 遇到的问题直接并不好解决,但是发现将原问题拆分成其子问题之后,子问题与原问题有相同的解法,等子问题解 决之后,原问题就迎刃而解了。
3.2 递归的概念
一个方法在执行过程中调用自身, 就称为 "递归".
递归相当于数学上的 "数学归纳法", 有一个起始条件, 然后有一个递推公式.
例如, 我们求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)!
递归的必要条件:
1. 将原问题划分成其子问题,注意:子问题必须要与原问题的解法相同
2. 递归出口
代码示例: 递归求 N 的阶乘
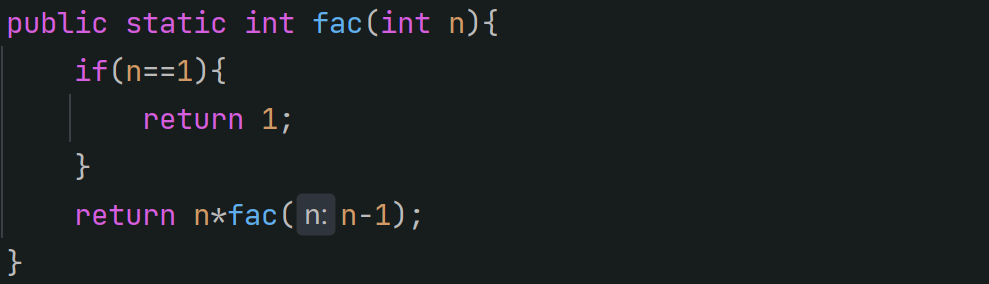
3.3 递归执行过程分析
递归的程序的执行过程不太容易理解, 要想理解清楚递归, 必须先理解清楚 "方法的执行过程", 尤其是 "方法执行结束 之后, 回到调用位置继续往下执行".
public class Test{
public static void main(String[] args) {
int n = 5;
int ret = factor(n);
System.out.println("ret = " + ret);
}
public static int factor(int n) {
System.out.println("函数开始, n = " + n);
if (n == 1) {
System.out.println("函数结束, n = 1 ret = 1");
return 1;
}
int ret = n * factor(n - 1);
System.out.println("函数结束, n = " + n + " ret = " + ret);
return ret;
}
}
执行过程图

程序按照序号中标识的 (1) -> (8) 的顺序执行
关于 "调用栈"
方法调用的时候, 会有一个 "栈" 这样的内存空间描述当前的调用关系. 称为调用栈.
每一次的方法调用就称为一个 "栈帧", 每个栈帧中包含了这次调用的参数是哪些, 返回到哪里继续执行等信息.
后面我们借助 IDEA 很容易看到调用栈的内容.
3.4 递归练习
代码示例1 按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4)
public class Test {
public static void print(int n) {
if (n >= 10) {
print(n / 10);
}
System.out.print(n % 10 + " ");
}
public static void main(String[] args) {
print(1234567);
}
}
代码示例2 递归求 1 + 2 + 3 + ... + 10
public class Test {
public static int sum(int n) {
if(n==1){
return 1;
}
return n + sum(n-1);
}
public static void main(String[] args) {
int ret = sum(10);
System.out.println(ret);
}
}
代码示例3 写一个递归方法,输入一个非负整数,返回组成它的数字之和. 例如,输入 1729, 则应该返回 1+7+2+9,它的和是19
public class Test {
public static int add(int n) {
if (n < 10) {
return n;
}
return n % 10 + add(n / 10);
}
public static void main(String[] args) {
int ret = add(12345);
System.out.println(ret);
}
}









![[Round#14 Illuminate with your bril]](https://img-blog.csdnimg.cn/a3ca2d9e3f8745d49cf78412f382e881.png)