归并排序

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分（divide）成一些小的问题然后递归求解，而治（conquer）的阶段则将分的阶段得到的各答案“修补”在一起，即分而治之）。

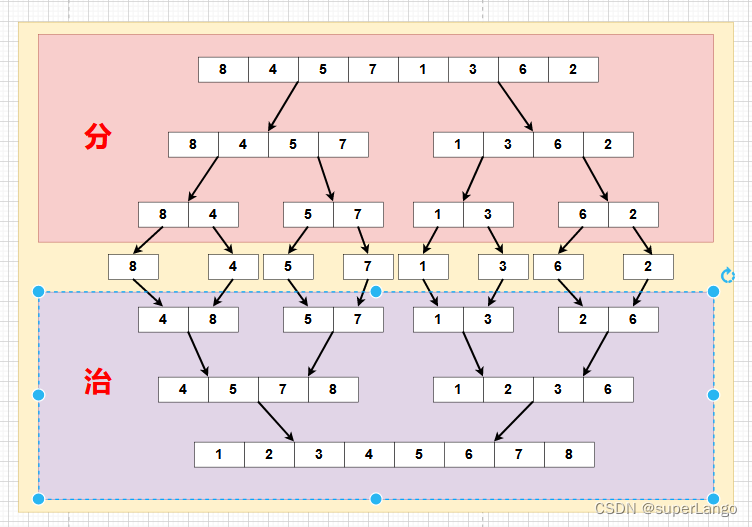
说明：

可以看到这种结构很像一颗完全二叉树，本文的归并排序我们采用递归去实现（也可以采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程。

代码实现：

public class MergerSort {
    public static void main(String[] args) {
        int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
        int[] temp = new int[arr.length];
        mergeSort(arr, 0, arr.length - 1, temp);
        System.out.println(Arrays.toString(arr));
    }

    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2; // 中间索引
            // 向左递归进行分解
            mergeSort(arr, left, mid, temp);
            // 向右递归进行分解
            mergeSort(arr, mid + 1, right, temp);
            // 到合并
            merge(arr, left, mid, right, temp);
        }
    }

    /**
     * 归并排序（合并）
     *
     * @param arr   排序的初始数组
     * @param left  左边有序序列的初始索引
     * @param mid   中间索引
     * @param right 右边索引
     * @param temp  中转数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left; // 初始化 i，左边有序序列的初始索引
        int j = mid + 1; // 初始化 j，右边有序序列的初始索引
        int t = 0; // 指向 temp 数组的当前索引

        // 一、
        // 先把左右两边（有序）的数据按照规则填充到 temp 数组
        // 直到左右两边的有序序列，有一边处理完毕为止
        while (i <= mid && j <= right) {
            // 若果左边的有序序列的当前元素，小于等于右边有序序列的当前元素
            // 即将左边的当前元素，填充到 temp 数组
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { // 反之，将右边的当前元素，填充到 temp 数组
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }

        // 二、
        // 把剩余数据的一边的数据依次全部填充到 temp 数组
        while (i <= mid) { // 左边有序序列还有剩余元素
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }

        while (j <= right) { // 右边有序序列还有剩余元素
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }

        // 三、
        // 将 temp 数组的元素拷贝到 arr
        // 注意：并不是每次都拷贝所有
        t = 0;
        int tempLift = left;
        while (tempLift <= right) {
            arr[tempLift] = temp[t];
            t += 1;
            tempLift += 1;
        }
    }
}

性能测试：

 public static void main(String[] args) {
        int[] arr = new int[8000000];
        for (int i = 0; i < 8000000; i++) {
            arr[i] = (int) (Math.random() * 8000000); // 生成一个 [0,8000000) 随机数
        }
        int[] temp = new int[arr.length];

        long start = System.currentTimeMillis();

        mergeSort(arr, 0, arr.length - 1, temp);

        long end = System.currentTimeMillis();
        System.out.println("通过归并排序的时间：" + (end - start)); // 1504ms
    }